利用示波器实现基本的抖动测量

抖动是数字信号时序相对于其标称值的短期变化。抖动主要有两种类型，随机抖动和确定性抖动。随机抖动是无界的，也就是说，其值随着测量持续时间的增加而持续增加，随机抖动与噪声等随机过程有关。而确定性抖动是有界的，随着观测时间的增加，其抖动幅度是限定的。确定性抖动进一步细分为周期抖动、数据相关抖动和有界不相关抖动（BUJ）。

让我们从时钟抖动测量开始。所讨论的时钟是一个133MHz的时钟，其振幅为150 mV，占空比为50%。为了与源阻抗匹配，采用50欧姆耦合将该时钟连接到示波器。图1显示了示波器上显示的时钟波形。

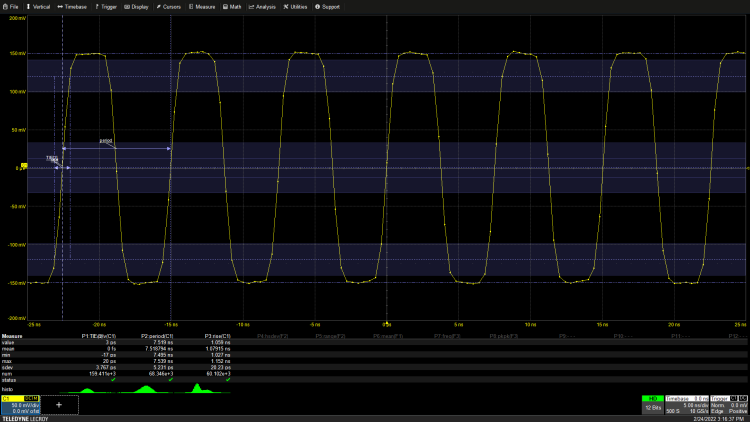
图1：测量时间间隔误差、周期和上升时间（包括测量统计）的133 MHz时钟。

测量参数

示波器的测量参数用于量化抖动。两个常用参数是周期和时间间隔误差（TIE）。

周期测量的是具有相同斜率的相邻边沿之间的间隔时间。而TIE参数测量的是数据边沿与其理想位置之间的时间差。TIE可以被认为是报告数据流的瞬时相位。TIE测量需要知道数据流的时钟频率。该频率可以明确地输入，也可以在TIE建立期间由示波器测定。

测量统计

本例中，时钟周期、时间间隔误差和上升时间的测量是在数千次采集样本上进行的。显示的测量统计包括最终测量值、平均值、最小值、最大值、标准方差（sdev）以及统计测量数。示波器记录每一次测量。每次采集显示波形中，包含五个完整的周期和七个上升沿，因此每次采集有五个周期测量和七个TIE和上升时间测量。

标准方差是一个统计数字，显示测量值的均值分布。计算取测量值（xi），减去平均值（µ），这本质上显示了瞬时周期抖动，再对这个差值取平方。计算总测量次数（N）上的平方差平均值，然后再对该平均值取平方根。

对于与该时钟信号相关的周期或TIE抖动来说，标准方差是一个很好的表征。实际上，它是周期或TIE抖动的均方根（rms）值。最大值和最小值之间的差值正是所选参数的峰值抖动。

注意TIE和周期的rms抖动之间的差异。这种差异是意料之中的，因为TIE测量单个波形边沿，而周期测量两个边沿之间的差。在这样的情况下，每条边上的抖动是随机的，并且假设独立，而周期测量中的抖动是每个边沿上抖动的平方和。预计周期抖动大约等于TIE抖动值2倍的平方根。

采样率

增加上升时间测量是为了确保示波器的采样率足够高，以清楚地定义时钟信号的边沿。边沿至少应有两个以上的样本。为了在1ns上升时间内有两个样本，采样率应大于2GS/s。

该测量中使用的50纳秒短记录可以显示20兆赫或更高频率的抖动变化。

为了使抖动与可能的低频源相匹配，需要获取更长的数据记录。这应该在保持示波器采样率为固定值的同时进行。该示例使用每秒10千兆个样本（GS/s）的采样率，因为水平刻度增加到每格50毫秒，如图2所示。

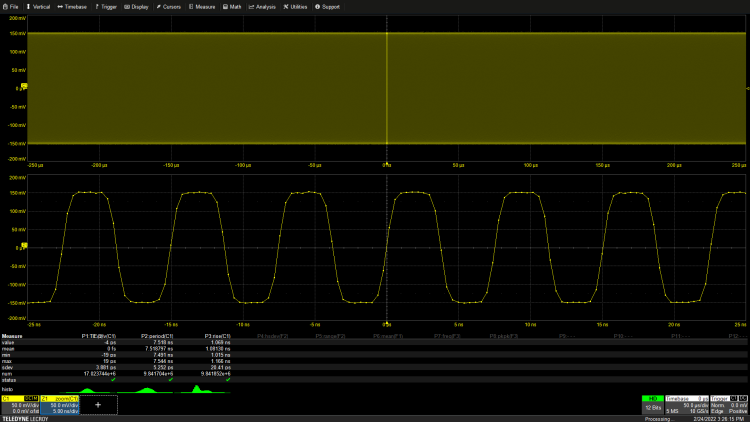
图2：通过将采集内存长度增加到5兆样本来增加采集持续时间。水平刻度增加到每格50毫秒。

这可以测量低至2 kHz的抖动变化。水平扩展的迹线变焦Z1，用于查看原本每格5ns的波形部分以及实际采集情况。即使长时间采集，也能测量获取的时钟信号中每个周期信号的TIE、周期和上升时间。该周期的标准方差保持在5.2ps，而TIE的标准方差保持在3.8ps。

对于时钟抖动，选择使用TIE或周期测量，通常取决于用户测试的标准。基于周期的抖动测量通常用于确认时钟信号。而TIE测量即可用于时钟信号，也可用于数据信号。

直方图

每个测量值下方的图标表示测量值的直方图。点击该图标将使直方图显示在数学跟踪中，如图3所示。

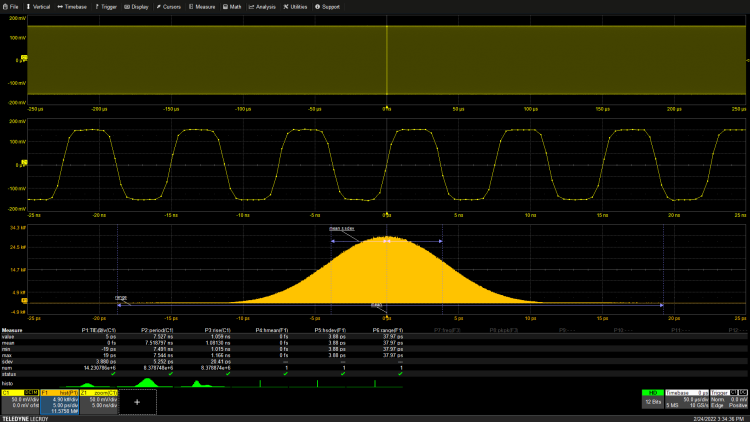
图3：直方图显示了所测TIE值的分布，分布的形状与抖动的来源有关。

直方图绘制了位于称为 bin 的狭窄范围内的测量值数量。在此示例中，直方图使用 2000 个间隔均匀超过 50 ps 的窗口(bin)，因此每个 bin 的宽度约为 25 fs。直方图的形状与周期抖动的来源有关。TIE 值的钟形具备高斯或正态分布的特征。这种类型的分布与诸如噪声之类的随机过程相关联。可以使用直方图对参数进行量化，在这种情况下，直方图采用均值、标准方差和范围。直方图上的蓝线是参数标记，显示每个参数的测量位置。如图3所示，对于这种高斯分布，68% 的测量值在平均值的 ± 1 标准方差范围内。标准方差越低，越接近测量值分布的平均值。

跟踪函数

基本抖动分析工具箱中的最后一个工具是跟踪功能。跟踪功能绘制每个测量值与时间的关系。迹线与源波形时间同步，因此迹线上的每个点都与产生该值的测量边沿或周期发生在同一时刻。测得的抖动中的任何周期性变化都将显示在跟踪功能上。在图 4中，TIE 的跟踪功能被添加到显示屏幕上。

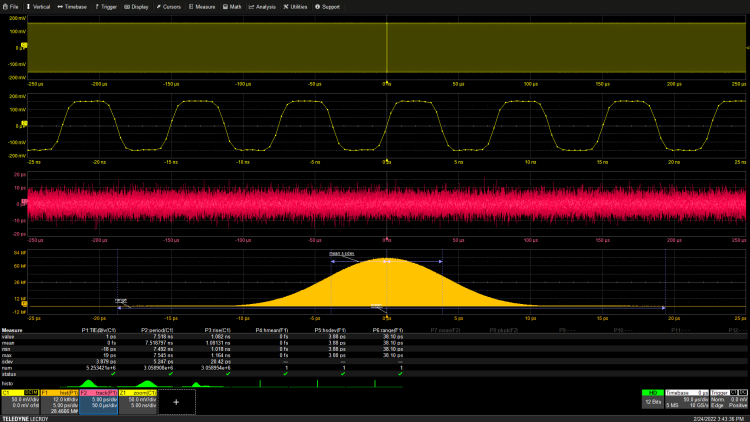
图4：跟踪功能显示了TIE测量随时间的变化，与通道C1中采集的波形同步。

TIE 跟踪功能的垂直刻度以时间为单位，显示采集波形每个周期与理想边沿位置的瞬时偏差。在此示例中，迹线是平坦的，因为抖动是随机噪声，没有明显的周期性。如果存在如图 5所示的周期性抖动，则迹线会更有趣。

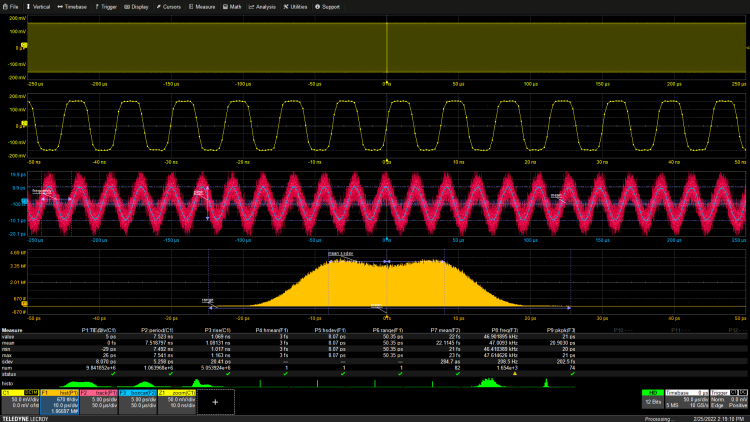
图5：测量具有随机和周期性TIE抖动分量的时钟。迹线显示时变周期分量。

向时钟抖动中添加 一个47kHz 正弦分量，直方图将会变为双峰形状。正弦波的直方图是马鞍形的，它与高斯分布的钟形进行卷积，形成观察到的双峰形状。峰值的分离与周期性抖动分量的幅度成正比。跟踪函数揭示了添加到随机分量中的正弦抖动分量的形状。应用于叠加在迹线上的迹线函数（数学迹线 F3 中的蓝色迹线）的 boxcar 平滑函数，可衰减随机抖动分量引起的噪声，并显示正弦抖动分量的平滑版本。测量参数 P7 和 P8 读取周期分量的频率和峰值幅度，分别为47 MHz和 20 ps 。

我们使用示波器中的抖动测量工具对时钟抖动进行了一些基本测量。这些测量经过一些修改后，可用于测量数据信号的抖动，如图 6所示。

图6： NRZ 数据信号的抖动分析使用参数时间间隔误差。用于分析时钟抖动的相同工具也可用于测量数据流上的抖动。

时钟频率为 133 MHz 的不归零 (NRZ) 数据流是该分析的来源。示波器设置保持不变，采集窗口为 500ms，采样率为 10 GS/s。缩放迹线显示部分 PRBS 7 数据。与时钟波形不同，数据波形没有统一的周期，故抖动分析时周期参数不适用。在测量时钟抖动的情况下，数据抖动将使用 TIE 参数的标准方差作为抖动量度的rms值。在此测量中，TIE 的标准方差为 3.9 ps。TIE 抖动的平均值仅为 3 fs，这意味着抖动平均值接近于零。

在时钟抖动的情况下，直方图和跟踪工具提供了额外的洞察力。直方图以零为中心，这与TIE参数的平均值一致。直方图范围为36 ps，并且在0左右对称。迹线函数基本上显示了一个关于平均值基本为零的的随机变化。叠加的boxcar滤波器输出显示出很小的4ps峰间变化，即使没有周期性抖动。这是与数据流相关的依赖于数据抖动的结果。这是一种与数据模式相关的确定性抖动。

与时钟抖动的情况一样，直方图和跟踪工具提供了额外的洞察力。正如从 TIE 参数的平均值所预期的那样，直方图以零为中心。直方图范围为 36 ps，并且基本上零对称。跟踪函数基本显示了一个数值大约为零的平均值的随机变化。即使没有周期性抖动，叠加的 boxcar 滤波器输出也显示出 4 ps 的小幅峰峰值变化。这是与数据流相关的数据抖动的结果。这是与数据模式相关的确定性抖动的一种形式。

如果将周期性抖动添加到数据流中，我们会看到与使用时钟抖动观察到的相似结果，如图 7所示。

如果将周期性抖动添加到数据流中，我们也会看到与图7所示的时钟抖动类似的结果。

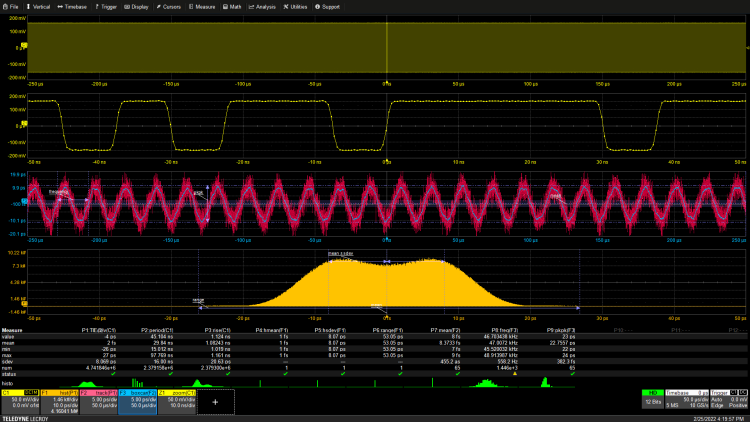
图7：对具有随机和周期性抖动分量的 NRZ 数据流的抖动分析。同时也存在数据相关的抖动。

周期性抖动元素的附加导致抖动直方图变为双峰，正如在时钟抖动情况中观察到的那样。跟踪函数显示周期性抖动分量的失真正弦波形。这与将周期性分量添加到时钟波形时发生的情况不同。

失真是由于附加了数据相关的抖动，这与数据模式有关。所有这些成分都包含在 TIE 测量的标准方差中。

基本抖动测量从时序参数 TIE 和周期开始。参数统计可提供rms和峰峰值两种抖动读数。参数的直方图提供了对抖动类型及其分布的深入了解。最后，跟踪功能有助于识别抖动中的周期性。抖动测量取自统计“num”字段报告的多个测量值，在大多数情况下该值少于 10⁸个。

 大多数示波器都提供更高级的抖动分析或串行数据分析软件，可对测量的抖动值进行外推，并可对10¹²及更高次数的抖动测量进行建模。它们还提供具有相关眼图分析的眼图显示。这些功能通常对串行数据的一致性测量非常有用。

(参考原文：Basic jitter measurements using an oscilloscope ）

本文为《电子工程专辑》2022年6月刊杂志文章，版权所有，禁止转载。点击申请免费杂志订