利用插值改进数字示波器的测量精度

众所周知，数字示波器是数据采样型仪器，无法捕获输入信号的连续记录。根据采样理论，如果用超过信号带宽两倍以上的速率对输入信号进行采样的话，该输入信号就可以根据采集的样本而被恢复出来。那么，存在存储器中的采集样本是如何被转换成连续信号的呢？此外，如何对采样的数据值进行准确的测量？最后，我们又如何测量小于采样周期的时间间隔？这些问题的答案很简单，插值！

显示插值

插值是在采集的信号样本之间添加计算得到的样本点。这个过程可以增加有效采样率，但不会增加所采信号的带宽。插值的效果是填充波形中的间隙，如图1所示。

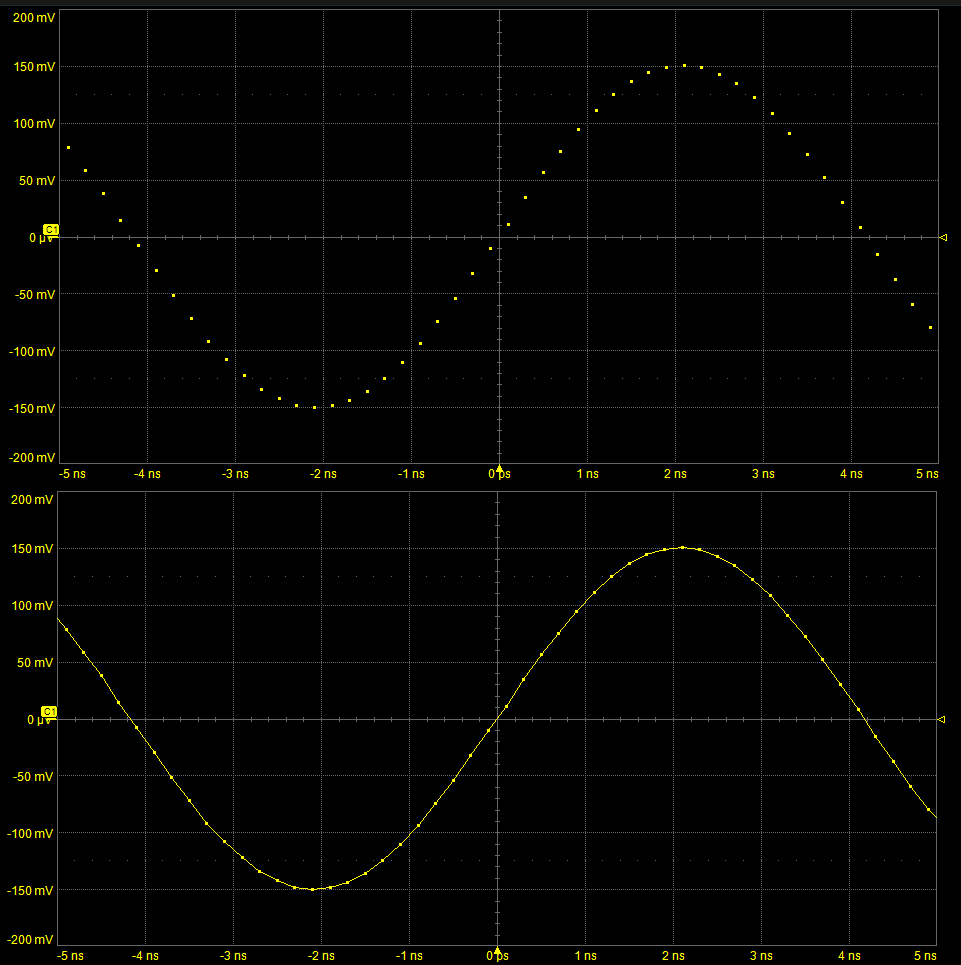
图1：上方迹线仅描绘了由实际采样点组成的信号。下方迹线显示的是启用插值后的同一信号。插值点填充在高亮显示的真实采样点之间的间隙中。

大多数数字示波器显示有两种插值方法可供选择，即线性插值或sin(x)/x插值。插值方法通常在输入设置中进行选择。在本文案例所用的示波器中，每个输入通道都可以单独控制选择该通道的插值方式，而在其他示波器中，插值是统一选取的，即选择某一方式后，所有采集通道将统一采用该方式。线性插值基本上是假设用一条直线连接两个真实样本，可以通过将三角窗函数与信号进行卷积来实现，具体实现方法之一是使用适当配置的数字滤波器。

Sin(x)/x插值所用的方法是将Sin(x)/x函数与信号进行卷积。时域中的sin(x)/x(或SINC)函数具有低通滤波器的频谱，如图2所示。

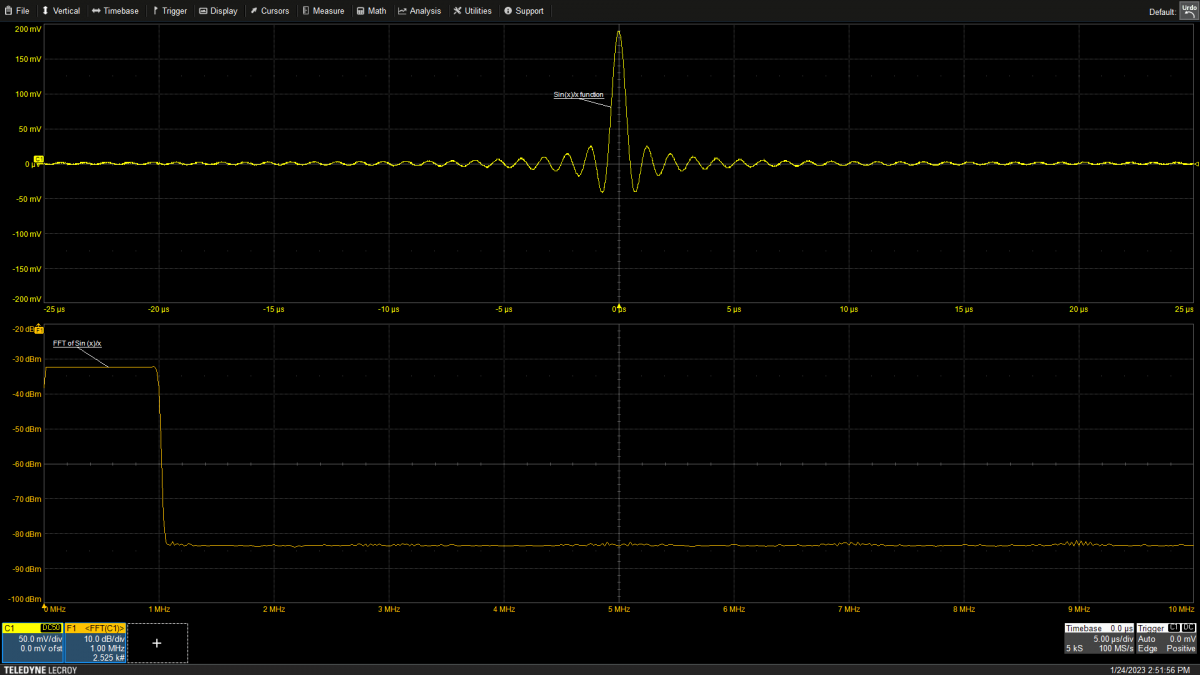
图2：时域中的sin(x)/x函数(上方迹线)在频域中具有低通滤波器响应(下方迹线)。

sin(x)/x频率响应的带宽是sin(x)/x函数振荡周期的倒数。由于时域中的卷积相当于频域中的乘法，因此sin(x)/x插值的操作基本上就是一种低通滤波。

随着采样率与带宽之比或过采样率的增加，线性插值方法和sin(x)/x插值方法的有效性都会随之增加。对于给定的带宽，插值性能总是随着采样率的提高而提高。不过不同的插值方法在性能上有一些差异。当过采样率在10：1以上时，线性插值效果非常好。图3给出了不同过采样率条件下的线性插值示例。

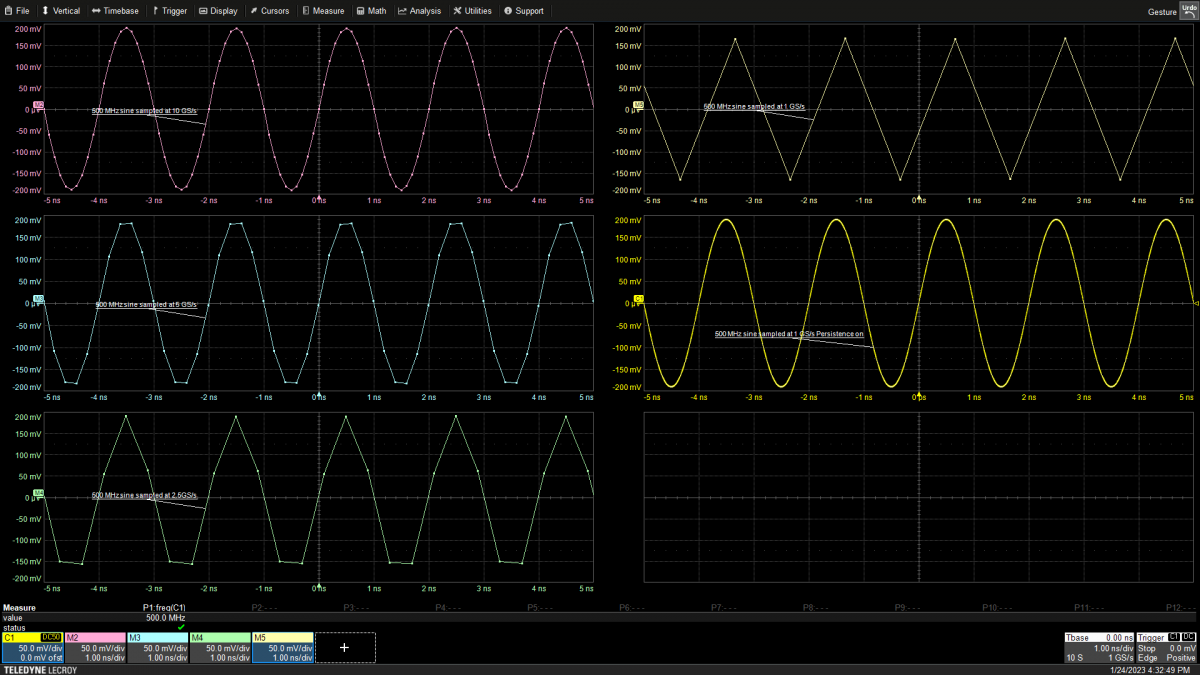
图3：线性插值器应用于500MHz正弦波的性能示例。过采样率分别为20:1(左上)、10:1(左中)、5:1(左下)、2:1(右上)。2:1情况下的余晖画面(右中)显示它仍然是一个正弦波。

虽然在视觉上并不“漂亮”，但所有版本在技术上都是正确的。如果开启无限余晖显示功能，那么当信号的不同相位被采样时，看起来不连续的波形将描绘出原始正弦波。使用余晖查看多次采集的历史数据是一种测试诀窍，在用低过采样率对波形进行采样时会很有用。

Sin(x)/x插值在过采样率超过2：1的情况下效果非常好。如图4所示，如果过采样率降至2：1以下，它们确实会出现问题。

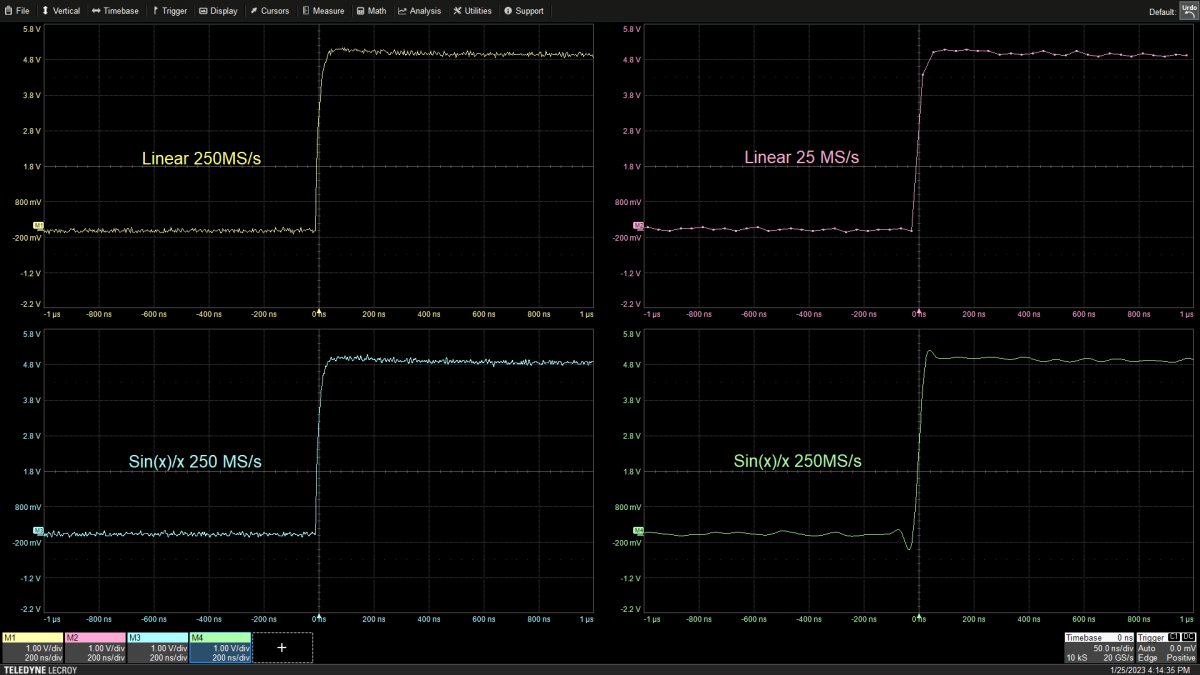
图4：对上升时间为27ns的阶跃函数应用线性插值(上方迹线)和sin(x)/x插值(下方迹线)的比较，采样率分别为250MS/s(左侧迹线)或25MS/s(右侧迹线)。

阶跃函数是一种较低频率的信号，由于存在中间的过渡而具有高频分量。阶跃函数的27ns上升时间具有13MHz的标称带宽。两种插值方法在250MS/s的采样率下都工作良好，此时的过采样率约为20:1。当采样率为25MS/s时，每个点的采样周期为40ns，略低于2:1的过采样率，此时线性插值器在边沿上只有一个样本，因此不能正确确定上升时间，不过波形基本上是正确的。sin(x)/x插值器在奈奎斯特极限以下运行时，会显示出并非波形上真实存在的预冲和过冲现象，这种效果被称为“吉布斯耳”。因此，在使用任何插值器时，关注采样率并确保其大于奈奎斯特极限是很重要的。

插值数学函数

本文使用的示波器也可以将插值作为数学函数使用。数学函数版本包括线性插值、sin(x)/x插值和三次插值。三次插值拟合样本之间的三阶多项式。就计算速度而言，它的性能介于sin(x)/x插值和线性插值之间。插值数学函数允许用户在采集的样本点之间选择介于2～50个插值样本之间的插值因子。图5给出了使用数学函数进行5:1插值的示例。

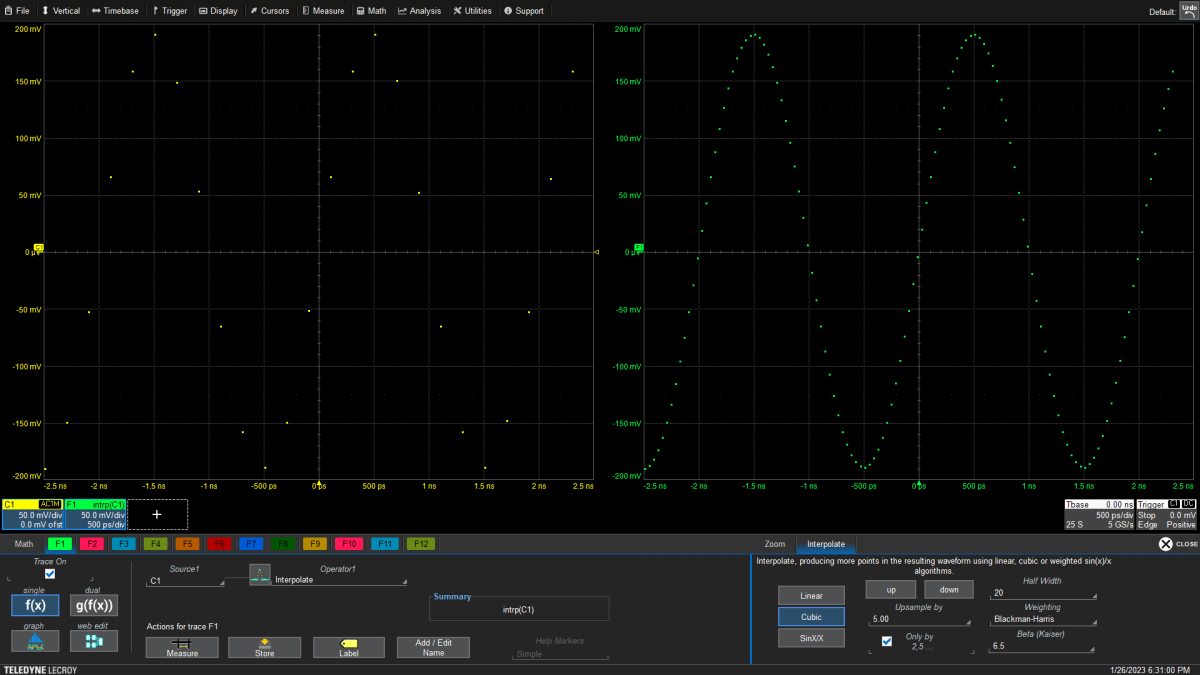
图5：用于插值器数学函数设置的控件，使用三次插值器可将样本数量增加五倍。

通过一系列大范围上的采样和各种控制，插值器数学函数为插值滤波器的定制化提供了更大的灵活性。与输入通道插值器不同，数学函数允许同时查看插值器的输入和输出，因此非常方便对响应正确与否进行检查。

插值数学函数允许用户增加波形中的样本数量，这在将信号应用于数字滤波器之前是有用的，因为滤波器的截止频率是采样率的函数。如下一节所述，它在表征波形测量方面也很有用。

测量插值

示波器中的时序测量是通过找到波形的电压阈值交叉处的时间点来完成的。相同斜率边沿交叉点之间的时间差形成一次周期测量。类似地，具有相反斜率的边沿之间的交叉时间差形成一次宽度测量。在许多情况下，信号的上升时间非常快，在比如20GHz的采样率下，边沿上只有几个样本。简单地在阈值附近的样本之间画一条线，是寻找交叉点的最简捷选择。然而，当样本在阈值两侧不对称分布时，可能会导致较大误差。在测量过程中可以使用内部插值来更精确地定位测量阈值交叉点，其精度比采样周期间隔好得多。这种测量过程会使用双插值，其中三次插值用于在采集的样本之间添加样本，阈值交叉时间通过阈值两侧两个插值样本之间的线性插值来确定，如图6所示。

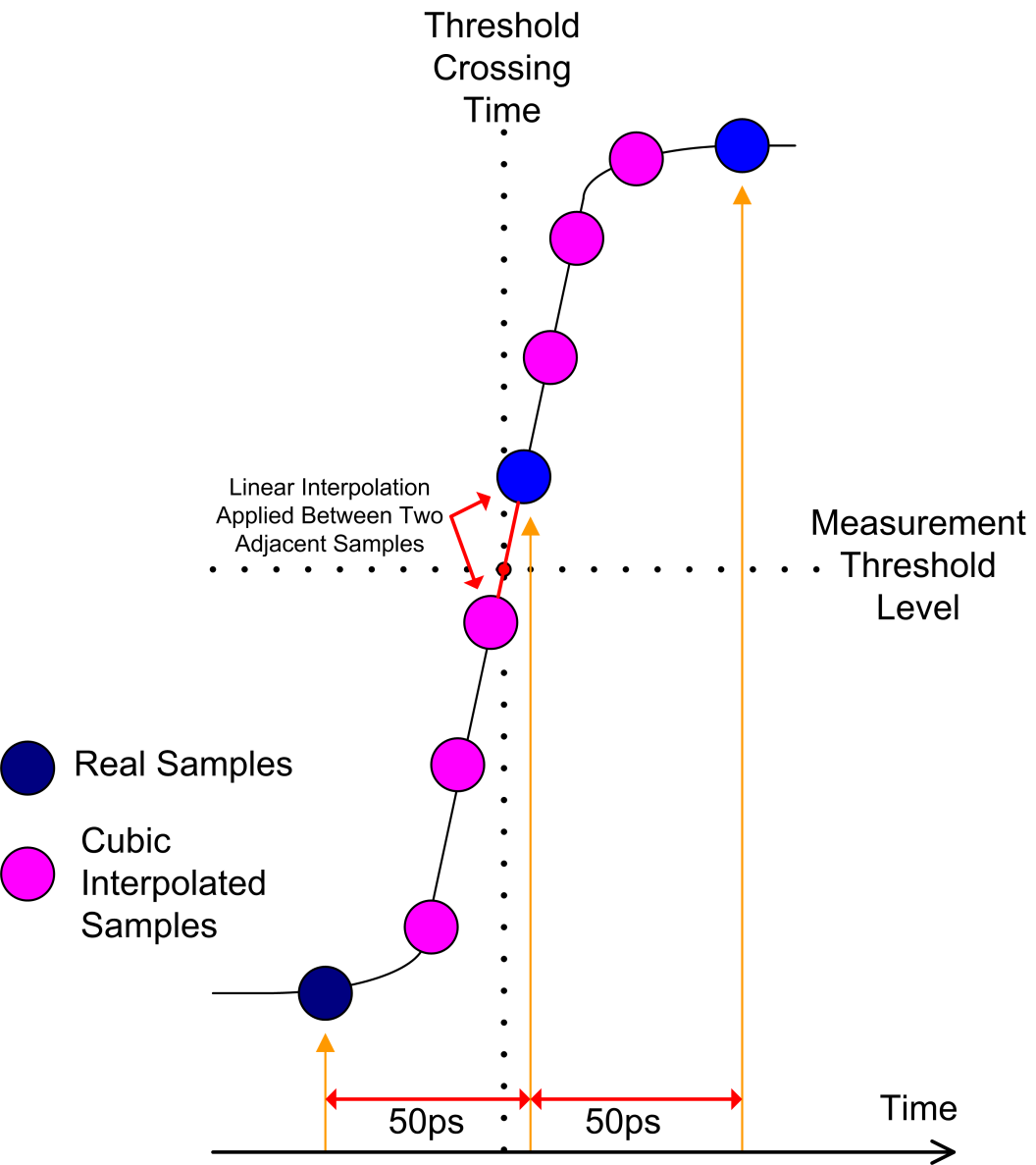
图6：将三次插值与线性插值相结合，可以提高数字示波器内部时序测量的时间分辨率。

时间是在波形幅度超过预定阈值的点位测量得到的。样本以采样间隔(本例中20GS/s时为50ps)隔开。先对波形使用三次插值，然后对最接近交叉点的点进行线性插值，就可以找到阈值交叉的确切时间。与以采样周期间隔的原始样本相比，采取这种方式所得到的测量结果具有高得多的时间分辨率。与sin(x)/x插值相比，使用三次插值具有更高的计算效率，并且精确插入样本的计算速度也更快。

时基插值器

测量触发事件和采样时钟之间子采样时延的插值器，则是一个人们不太熟悉却又更重要的插值器。通常，触发事件与示波器的采样时钟是异步的。每次采集的采样相位或水平偏移都是随机的。如果要对从触发器到第一个样本的时间进行直方图处理，它将在0和1样本周期之间呈现均匀分布。由于随机性水平偏移，多个波形的余晖画面可以显示样本点的所有可能位置，如图3所示。

稳定的触发式显示要求每个采集的波形迹线与触发点在完全相同的时间位置对齐。对于没有触发延迟偏移的时基，触发位置通常在时间零点。触发器和采样时钟之间的时间差测量，是通过使用一种名为时间数字转换器(TDC)的设备来测量时延而完成的，这里的TDC基本上是一种高分辨率计数器。这个时延就是波形的水平偏移。当显示波形时，水平偏移用于排列来自多次采集的触发信号，图7显示了一个复杂波形的六次采集。

图7：超声波波形的六次采集(上方网格)均使用缩放迹线进行了水平扩展，以便在下方网格中显示每条迹线的水平偏移。标签Z1到Z6指向(光标在t=0处标记的)每次触发之前的实际采样点。

使用水平缩放扩展了触发周围的区域，因此可以查看到六次采集的水平偏移变化范围，采样周期为20ns(50MS/s)。对于六次采集，在t=0触发之前，水平偏移在2.5～17.7ns之间变化，其位于前面讨论的一个样本周期范围内。TDC的时间分辨率取决于具体的示波器型号，并且与示波器的最大采样率有关。涉及TDC性能的示波器指标是“触发器和插值器抖动”。高性能示波器的指标通常小于2ps rms。示波器设计者会使用软件辅助触发对其进行改进，将该指标降至0.1ps以下。利用TDC与软件辅助触发，使抖动等与时间相关事件的精确测量成为可能。如果没有TDC硬件和软件，时间测量分辨率将受到采样周期的限制。

(参考原文：Filling in the blanks in digital oscilloscope waveforms）

本文为《电子工程专辑》2023年6月刊杂志文章，版权所有，禁止转载。点击申请免费杂志订阅