狄利克雷发明了一个新的数学领域和许多新的抽象方法。在这个证明中，他使用了一些现代抽象概念。应该注意的是，狄利克雷在他的证明中使用的符号与我们更现代的符号非常不同。他还首先证明了仅考虑素数模数的定理，由于群论的考虑，这更容易。
研究素数最强大的工具之一是狄利克雷特征理论——解析数论“之父”的一项伟大发明。然而，在解释它们是什么之前，我们将首先尝试理解为什么需要它们。
好主意
1805年的法国，诞生了一位天才。他的名字叫彼得·古斯塔夫·勒琼·狄利克雷。狄利克雷在 12 岁时就对数学产生了兴趣，并于 1822 年前往巴黎求学。
几年后，他证明了费马大定理的一个特例的一部分，即n = 5的情况。这使他在数学界名声大噪。必须考虑到，唯一解决的其他特殊情况是费马自己解决的n = 4和欧拉解决的情况n = 3。所以这是一件大事。它还显示了 Dirichlet 对数论的兴趣，这在后来变得很明显。
1826 年，狄利克雷移居柏林，在那里他开始产生有趣的成果，并为学生提供了引人入胜的教育。1832年，狄利克雷成为普鲁士科学院最年轻的院士，年仅27岁。
然后在 1837 年，狄利克雷开始思考一个将彻底改变我们研究整数的方式的问题。数学家们知道有无限多个素数（欧几里得在公元前 300 年证明了），但在当时研究自然数有趣子集中的素数似乎遥不可及。但后来狄利克雷有了一个好主意。
当时的先驱们正在积极发展复分析领域，狄利克雷在这个新的热门领域拥有大量的分析工具。他的绝妙想法是使用这些工具来研究整数，从而将复分析和数论结合起来。
他想要解决的问题是以下陈述：
对于任意两个互质正整数 a 和 m，存在无限多个 a + nm 形式的质数，其中 n 是正整数。
数列{a + nm} = {a + m, a + 2m, a + 3m, …}称为算术级数。我们观察到序列中任意两个连续数字之间的距离是常数——在上面的例子中是m。
当没有素数可以整除两个整数时，我们将两个整数定义为互素（或互素）。上面关于素数的陈述中等差数列的这种限制是需要成立的，因为否则就会有一个素数除以数列中的所有数字，这当然意味着其中不可能有无限多个素数。
狄利克雷证明了这个命题，现在这个定理以他的名字命名。它被称为等差级数的狄利克雷定理。为了证明这一点，狄利克雷发明了一类完全可乘的函数，现在称为狄利克雷特征。狄利克雷给出的证明不仅定义了解析数论的新课题，而且是证明实际上比定理说的更多的情况。稍后会详细介绍。
狄利克雷特征
令m为自然数。模数为m的狄利克雷特征是一个函数 χ: ℤ → ℂ 从整数到满足以下陈述的复数。
x(ab) = x(a)x(b)。
如果gcd(a, m) > 1则χ(a) = 0否则χ(a) ≠ 0。
χ(a + m) = χ(a)。
从这些属性中，可以导出其他几个属性。例如，根据上面的第二个属性χ(1) ≠ 0，无论模数如何，因此我们可以除以它，所以我们有χ(1)χ(1) = χ(1⋅1) = χ(1)其中意味着所有字符的χ(1) = 1。所以我们有
5. 对所有的 χ(1) = 1。
6. 我们看到χ(-1)² = χ((-1)²) = χ(1) = 1，因此χ(-1) = 1或χ(-1) = -1。
我们称这个标志为性格的平价；如果χ(-1) = 1，则称该字符为偶数，如果χ(-1) = -1，则称其为奇数。
请注意，对于任何模数m，我们都有一个特殊字符，称为主字符χ0 mod m。它由以下定义
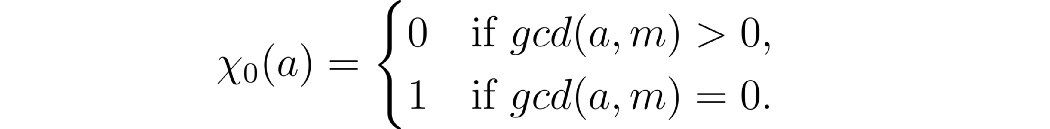
此外，我们有一个开箱即用的明显事实。回想一下a ≡ b (mod m) 当且仅当 m | a - b这里的符号表示m 除 a - b。
7. 如果a ≡ b (mod m)则上面的第三个属性表示χ(a) = χ(b)。
其他几个属性是可推导的。特征符最重要的性质之一是它们都是乘法群之间的同态，因此在复平面的单位圆上取值。我们不会在这里讨论字符的组方面，但是有丰富的理论可以将它们推广到除整数mod m的单位以外的组。
在我们继续之前，我们还需要知道两件事。
第一个是以伟大的数学家莱昂哈德·欧拉命名的算术函数，称为欧拉总 函数ϕ。我们定义ϕ(n)为小于n的互质正整数的个数，即。自然数 k < n 使得 gcd(k, n) = 1。例如，ϕ(10) = 4因为有4个小于 10 的自然数与 10 互质。
我们需要的第二件事是关于狄利克雷特征的事实，称为正交关系。
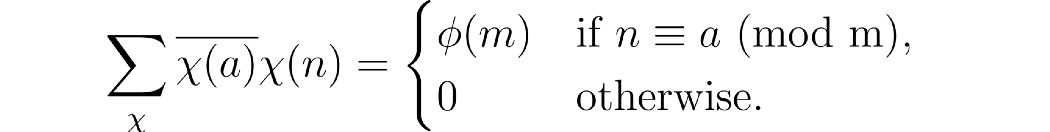
这里的总和是在所有具有模数 m的字符上，第一个字符上的横线是字符的复共轭，这仅仅意味着我们改变了χ(a)的虚部的符号。
从欧拉到 L 函数
与许多伟大的数学故事一样，这个故事从欧拉开始。
欧拉研究了 zeta 函数（定义如下）并发现了素数和自然数之间的美妙联系，称为欧拉积。结果如下，让s > 1，然后
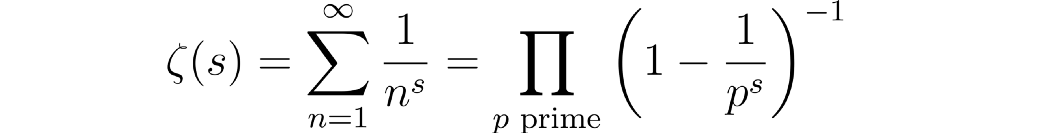
其中右侧的产品接管所有质数。第一个方程是定义，第二个是已证明的定理。
s 实际上可以是一个复数，但在欧拉的时代，复数分析还处于起步阶段，他只考虑s 的实数值。这里定义的函数就是著名的zeta 函数。
这实际上给了我们另一个证明，即有无限多个素数！如果我们让s → 1，左侧趋于无穷大使得右侧也发散，但这只有在乘积包含无限多个因子时才有可能。
其实，仔细考察一下，还可以多说一点。欧拉指出，如果你对等式两边取对数，就会发生一些有趣的事情。
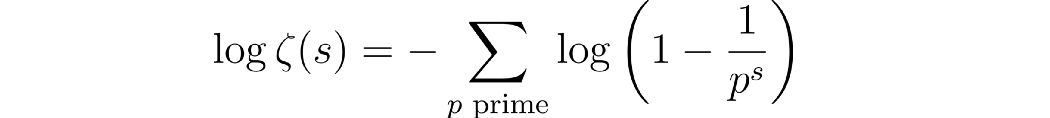
这里的log表示自然对数。现在，回想一下对数的泰勒级数展开
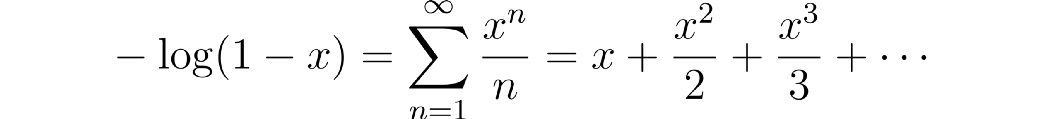
其中 x 允许取[-1, 1)区间内的值以使右侧的级数收敛。在我们的log ζ表达式中，当s > 1并且任何素数都大于1时，我们就有这样的例子。这样我们得到
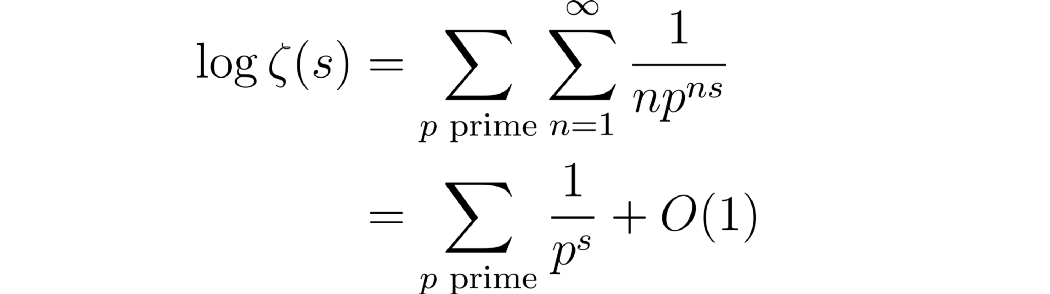
从右边s → 1 。
最后一个表达式只是一种奇特的说法，即log ζ(s) = ∑ 1/p^s加上某个有界函数（有界意味着对于某个正实常数 M，绝对值小于 M）。
有很多方法可以证明这个渐近界。一种方法是回到对数和。我们可以通过微积分的各种方法证明，如果0 < x ≤ 1/2那么-log(1 - x) < x + x²。在下雨的下午，这实际上是一项很好的锻炼！
由于1/p^s ≤ 1/2对于所有素数p和s > 1，我们可以使用这个小引理并代入得到
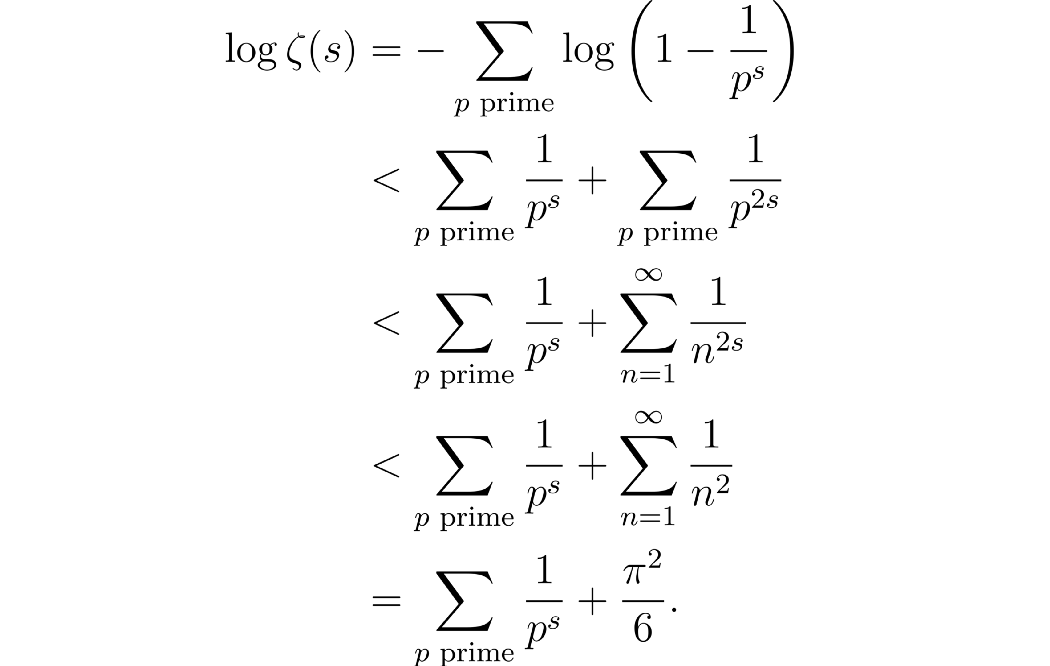
这显示了欧拉对巴塞尔问题的著名解决方案的明确界限和很好的应用。
通过这种更仔细的方法，我们已经确定不仅有无限多个素数，而且素数上的级数∑ 1/p发散！
通过这种方式，我们可以自信地说，在自然数中，素数比平方更密集。
尽管素数的倒数之和发散得非常慢。事实上，从上面我们可以看出，它的发散近似于log log x。
这是一个增长极其缓慢的函数。例如，要使这个函数超过数字 4，我们需要 x 大于 e^e⁴，这是一个 24 位数字！
狄利克雷的想法是试图将这个结果推广到素数的子集，即等差级数中的素数。请注意，以下等差数列 { n, n+m, n + 2m, n + 3m, …}可以表示为{k | k ≡ n (mod m)}。
换句话说，Dirichlet 想要证明如果gcd(a, m) = 1，我们得到的结果是
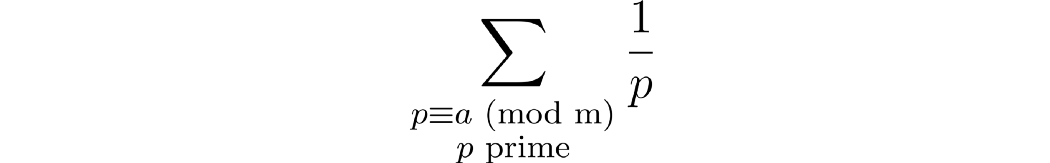
分歧。
为了做到这一点，狄利克雷有了第二个奇迹般的洞察力。事实证明，zeta 函数有许多表亲，它们显示出许多与 zeta 函数相同的属性，包括欧拉积。这类函数是狄利克雷的第二大发明！
由于狄利克雷特征完全可乘，其对应的狄利克雷级数也有欧拉积。具体来说，我们有关于字符 χ的狄利克雷 L 级数的定义。
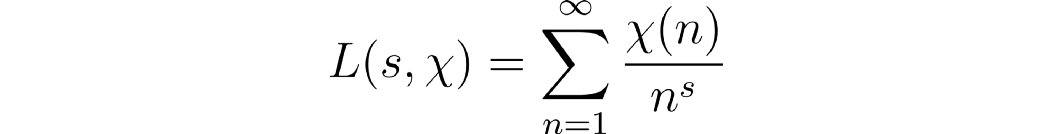
我们假设 s > 1。
这也可以为复数 s 定义，事实上，通过解析延拓，这个函数可以扩展为整个复平面上的亚纯函数，然后称为狄利克雷 L 函数。
当在复平面上定义 zeta 函数时，它被称为黎曼 zeta 函数。
由于所有狄利克雷特征都是完全可乘的，因此该级数也有欧拉积。
请注意，具有平凡特征的狄利克雷 L 级数的定义，即对所有 n 的 χ(n) = 1，为我们提供了通常的 zeta 函数及其欧拉积。这使得狄利克雷 L 函数成为 zeta 函数的推广。
事实上，这些函数与黎曼 zeta 函数非常相似，以至于它们不仅拥有等价的欧拉积，而且还围绕直线Re(s) = 1/2具有漂亮的对称关系。此外，它们有望满足黎曼猜想的等价陈述，但在撰写本文时尚未证明这一点。
在这些概括中，偶数字符和奇数字符之间存在一些区别，以及它们是否具有称为原始性的属性，但这有点超出本文的讨论范围。
狄利克雷证明
一旦 Dirichlet 建立了字符的欧拉积，下一个合乎逻辑的步骤就是再次对两边取对数以获得素数的总和。
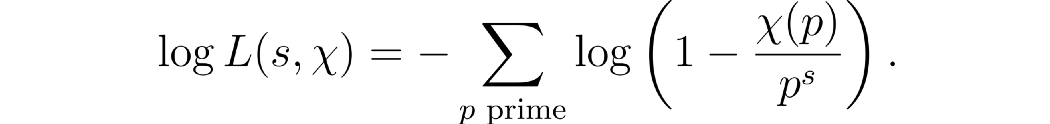
再一次，通过与上述类似的论证，我们可以使用渐近法将其重写为
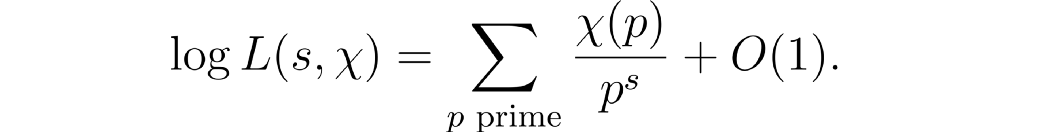
回想一下，这只是意味着当s 从右侧开始 → 1时，右侧的总和大致像左侧一样增长。该声明当然可以进一步形式化，但这是总体思路。
从这里狄利克雷有了一个好主意。他使用正交关系将其变成他想要的形式。具体来说，如果我们在上式两边乘以χ(a)的复共轭，然后对所有具有模数 m的字符求和，则我们得到以下结果。
这真太了不起了。狄利克雷使用他的特征定义了一个（全纯）函数作为算术级数{a, a + m, a + 2m, a + 3m, …}中所有素数的总和。
现在，狄利克雷“只”需要证明左侧发散为s → 1。
证明这一点的策略是通过将字符分组为三个不相交的集合（实际上，这是一个分区！）来将证明分成案例。
主要特征 χ0,
复数字符 (∃n: χ(n) ∉ ℝ),
二次字符（χ² = χ0，但 χ ≠ χ0）。
这样做的原因之一是对于任何非主要字符 χ 事实证明，序列L(s, χ)在s > 0时收敛。
该策略是证明L(s, χ0)在s = 1处有一个简单的极点，即相应的 L 系列发散，并且如果 χ 是一个非主字符，则 L(1, χ) ≠ 0。
第二个陈述的原因是我们需要确保 L(s, χ0) 的极点不会被“ log(0) ”这样的表达式形式的负无穷大吃掉。所以我们需要确保这两件事。
第一条命题很简单，可以通过多种方式证明。例如，可以检查
并观察到除以右侧模数 m的素数的乘积始终是有限的——实际上，您可以检查它是否等于ϕ(m)/m当s = 1时。因此，左侧的级数在s = 1处继承了 ζ 的极点。
因此，重要的是要证明对于任何非主要字符，L(1, χ) ≠ 0。
复杂的情况相对容易，因为如果我们对相应的 L 系列的所有字符进行乘积 ‖ L(s, χ)，那么首先，可以证明 ‖ L(s, χ) ≥ 1。可以做这是通过将 L 系列的对数写为另一个系列（涉及Von Mangoldt 函数），在这种情况下更容易处理。
其次，由于主要特征的 L 系列对于s → 1发散，乘积中最多只能有一个零因子，否则，它会是 0，与它大于1相矛盾。但是，如果 χ 是一个复数字符，那么它的复数共轭也是如此，并且它们是不同的，但如果一个为零，另一个也为零。因此，对于复数 χ，L(1, χ) ≠ 0。
二次情况有点微妙，超出了本文的范围。
小结
狄利克雷发明了一个新的数学领域和许多新的抽象方法。在这个证明中，他使用了一些现代抽象概念。应该注意的是，狄利克雷在他的证明中使用的符号与我们更现代的符号非常不同。他还首先证明了仅考虑素数模数的定理，由于群论的考虑，这更容易。
您可能感兴趣