使用1kΩ电阻能排列出几种阻值？

哪一位模拟设计师不需要使用标准电阻值的串联/并联组合来得到非标准的电阻值？为了避免在生产过程中用电位器进行微调，当我们需要精确的分压器时，可以使用0.1%的电阻器。

为了获得非标准值，采用串联两个或多个电阻的方法很有效——总电阻是它们的和，这样计算起来很容易。较大的电阻构成数值的主要部份，串联的小电阻用来实现微调。

即使是在日常生活中，也可能有机会修理到带开放式线绕散热电阻的旧真空管电子琴、心血来潮翻看零件箱，然后将一串5W电阻焊接在一起，从而解决一些难题。当然，在散热功能改善以后，它们在工作时的温度比原来更低得多。

并联电阻有点难以计算，因为R_TOTAL = (R₁ × R₂ ) / (R₁+ _R2 )。当选择将大数值电阻与小数值电阻并联焊接时，并联方式更适合手动微调稳压器之类的组件。虽然对于大规模生产来说并不是很好，但对于一些特殊的固定装置来说还可以，而且如果去除了可调电位器，将来就没有人会把校准给搞乱了。

Martin Rowe向我提出了这个小挑战：“仅使用1kΩ电阻，你能组合出多少种阻值排列？”

听起来很有趣，而且是我以前从未曾想过的。我的目的是最多用10个1kΩ电阻，以各种方式进行串联/并联。但是，当我才用到5个电阻时，可能的排列数已经变得势不可挡。

那么，n个1kΩ的电阻器可以进行多少种不冋的排列组合？

第一个明显的排列是全部串联和全部并联。当n = 2个电阻时，可能的排列是两个值(图1)。

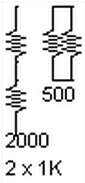
图1：2个电阻，2种组合。这很容易。

当n = 3时，有四种可能的排列。快速计算小诀窍：当所有电阻的阻值相同时，其等效电阻是将其值除以并联电阻的数量。将电路分解成小的串联/并联电阻对来计算最终的等效电阻，使用“对”会更容易进行并联计算(图2)。

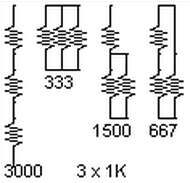
图2：3个电阻，4种组合。

当n = 4时，排列数量激增至9 (图3)。我想我已经包含了所有可能的情况，但是如果有人发现有任何遗漏，请让我知道。

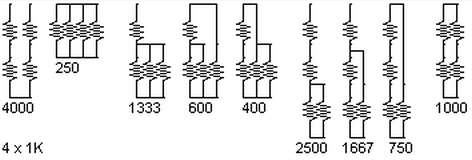
图3：4个电阻，9种组合。

最右边的组合阻值为1000Ω，等同于一个1000Ω的单电阻。使用四个电阻的优点是，功率耗散性能也提高了四倍，耐压翻倍。如果希望所有电阻是表面贴装类型，这一特性非常有用。

将n增加到5，如果我没有忽略任何一种组合的话，排列数将提高到23 (图4)。同样地，如果你发现有任何遗漏，请告诉我。

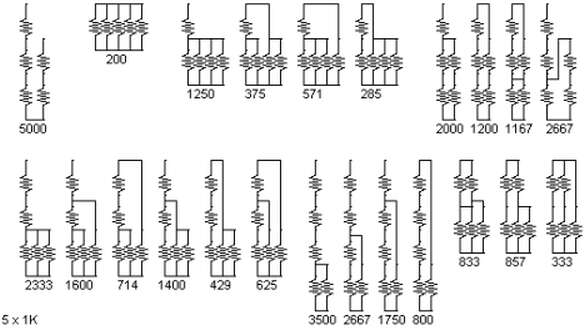
图4：5个电阻，23 种组合。有没有遗漏呢？

这时，我了解到如果增加到10个电阻，我是找不到足够大的纸来画它们的。也许你们当中有擅长数学的小伙伴能够计算出n个电阻的所有排列数？来吧！告诉我你的计算结果。

亲爱的读者们，你们能不能推导出一个适用于任何串并联电阻数的公式呢？欢迎留言告诉我。

编译：Jenny Liao

(参考原文：Resistor combinations: How many values using 1kohm resistors?，by Glen Chenier)

责编：Luffy Liu