第二级输出滤波器通常用来衰减开关电源的输出电压纹波，还可以用于负载电路之间的隔离。本文将介绍满足负载瞬态规范要求的典型设计规范。
第二级输出滤波器通常用来衰减开关电源的输出电压纹波，还可以用于负载电路之间的隔离。本文将介绍满足负载瞬态规范要求的典型设计规范。
这个设计示例是一个负到正的反相降压-升压转换器。图 1 是单相等效电路的简化电路图。德州仪器 (TI) 的功率放大器使用48V/25A的负到正同步降压-升压参考设计，其中包括四相 1,200W 转换器的完整设计和测试报告。
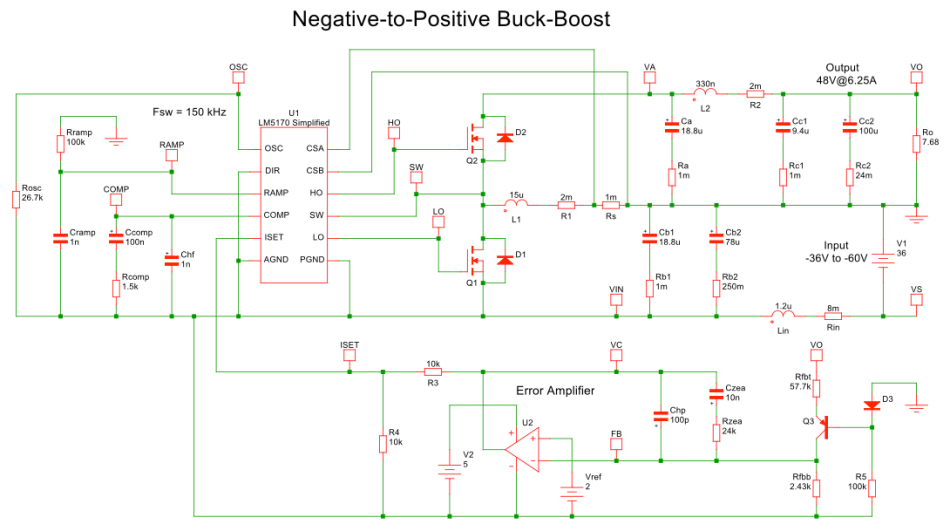图 1：用于仿真的300W 单相升/降压等效电路
上述应用对输出电容的电压纹波没有硬性要求，但由于输出纹波电流自身较大，还是需要对其进行一些合理的衰减。对于瞬态响应的设计，在负载电流 50% 阶跃的情况下，一般要求3%的输出电压偏差。
为了满足瞬态要求，需要确保输出滤波器的阻抗足够低，并且保证控制环路的带宽足够高，以便在负载电流阶跃期间将输出电压保持在容差范围内。
这样做的主要目标是将尺寸和成本最小化。首先第一步是根据均方根 (RMS) 电流额定值挑选陶瓷电容器，并将它们用作第一级。电感值需要足够高，用来在降低纹波电流的同时，保持合理的二阶峰值，以确保稳定性。为了瞬态保持，可选择铝聚合物电容器为第二级，与较小的陶瓷电容并联，这将提供足够的电阻来抑制滤波器。
设计方法和计算
需要确定输出电容器中的 RMS 电流，最坏的情况是输入最小且负荷最大。使用 Power Stage Designer 4.0，输出电容的纹波电流为 7.5 A。近似为公式 1：
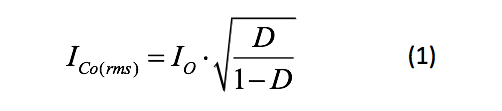其中 D为占空比，D = VO / (VO + η·VIN) ，η 为效率。
公式 2 将第一级陶瓷电容器上的纹波电压表示为：
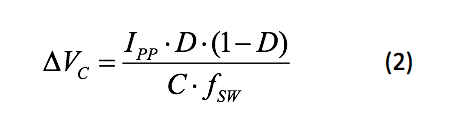
其中电容的峰峰纹波电流值为 IPP = IL +ΔIL / 2。
选择陶瓷电容来处理 RMS 额定电流问题很容易，因为 1206 或 1210 封装的额定电流大约为 3 A 到 6 A。您需要注意的是纹波电压，因为我们会根据纹波电压来确定所需的电容。负载瞬态的目标为 48V × 3% = 1.44V，我们将其作为第一级纹波电压。从Power Stage Designer 中可知 IPP = 19.3 A，求解公式2可得：C = (19.3 A·0.58·0.42) / (1.44V · 150 kHz) = 21.8μF，因此可使用五个 4.7-µF、100-V 的陶瓷电容器。
下一步是确定交流纹波电流衰减，用于确定电感值。由于第一级陶瓷电容器具有三角纹波电压，公式 3 为第二级电感纹波电流：
使用 20% 的衰减系数，电感的峰峰值纹波电流为 19.3 A × 0.2 = 3.86 A。电感值为 L = 1.44 V / (8 · 3.86 A · 150 kHz) = 310 nH，因此可以使用 330 nH的标准值。
图 2 展示了纹波电压和电流波形。
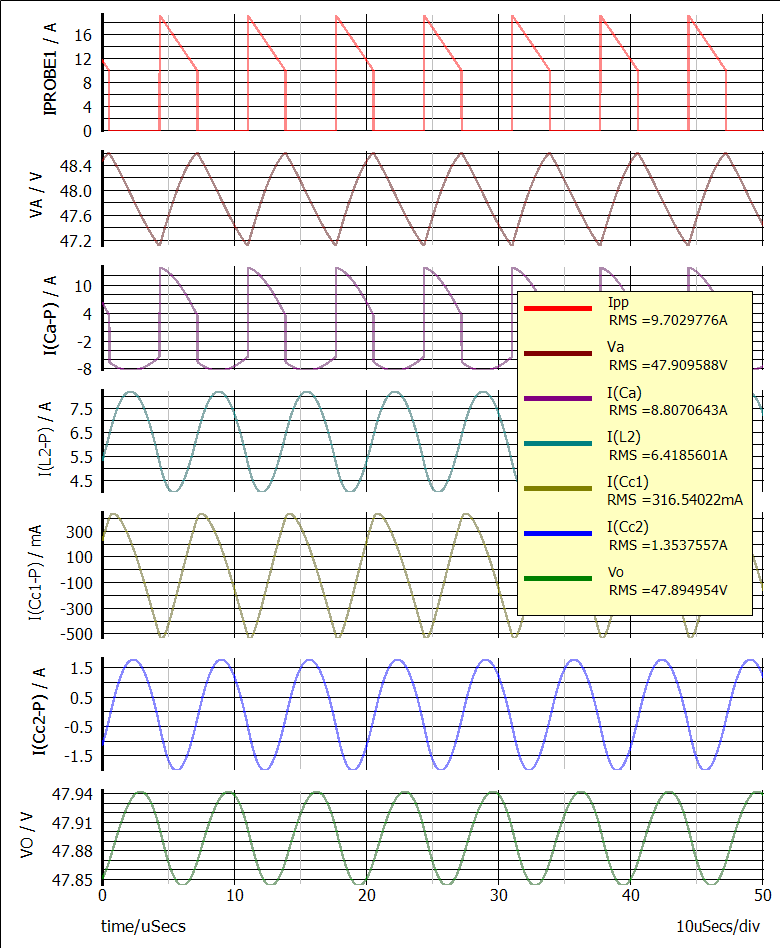图 2：第二级滤波器的仿真结果，显示了纹波电压和电流
为了满足瞬态负载的要求，首先要根据转换器的带宽确保总输出电容足以维持的输出电压。其次，要确保输出阻抗足够低，以将初始步阶保持在一定界限内。
为了确定输出电容，需要预估控制环路的带宽。对于更高功率的降压-升压转换器，电源阶的右半平面零点往往会是其限制因素。最坏的情况发生在以最小输入负荷最大负载时，这种情况可以在参考文献 1 中的演示文稿中找到，其中ƒRHPZ = (RO · (1–D)2) / (2 · π · L1 · D) = (7.68 Ω · 0.422) / (2 · π · 15 μH · 0.58) = 24 kHz。
由于第二级滤波器的固有峰值现象，需要额外的稳定裕度，因此需将控制环路带宽设置为右半平面零点的十分之一，以便 fC = 2.4 kHz。参考文献 2 中，COUT = IP / (2 · π · ƒC · VP)，其中 IP是负载电流阶跃，VP是输出电压的允许偏差。从图 1 中确定负载电流为 6.25 A，所需电容为 COUT = (6.25 A · 0.5) / (2 · π · 2.4 kHz · 1.44V) = 72 μF。
我们选择100μF 的铝聚合物电容器，它具有 24mΩ 的等效串联电阻和 3A 的RMS 电流额定值。再加两个 4.7μF 的并联陶瓷电容可产生额外的输出纹波电压衰减。
考虑到谐振频率和阻尼，现在要比较由滤波器阻抗引起的瞬态电压。在快速负载瞬变的过程中，铝聚合物电容的等效串联电阻决定了初始电压偏差： VP(Rc) = IP·RC = 3.125 A·24 mΩ = 75 mV，正好在3%的限制范围内。
谐振的串联等效电容为 Cs = (Ca · Cc) / (Ca + Cc) = (20 μF · 100 μF) / (20 μF + 100 μF) = 16.7 μF。
第二级滤波器的特征阻抗为 Zfilter = √ (L2 / Cs) = √ (330nH / 16.7 μF) = 140 mΩ。
谐振频率为 ƒres = 1 / (2 · π · √ (L2 · Cs) = 1 / (2 · π · √ (330nH · 16.7 μF) = 68 kHz)。
无功阻抗与实际阻抗之比将决定增益峰值：AVP = 20 · log(140mΩ / 24 mΩ) = 15 dB。
为了保障稳定性，您需要确保闭环中的峰值始终保持在单位增益以下。
闭环反馈回路
如要使用第二级滤波器形成控制回路，则有两个可能的反馈点。一个在第二级滤波器之前的转换器处，一个在滤波器的负载侧。我们需要确定这些反馈处（对应图 3 中的 Va和Vo）的阻抗。 在此分析中，将电流模式控制功率级输出看作电流源，负载为恒定电流。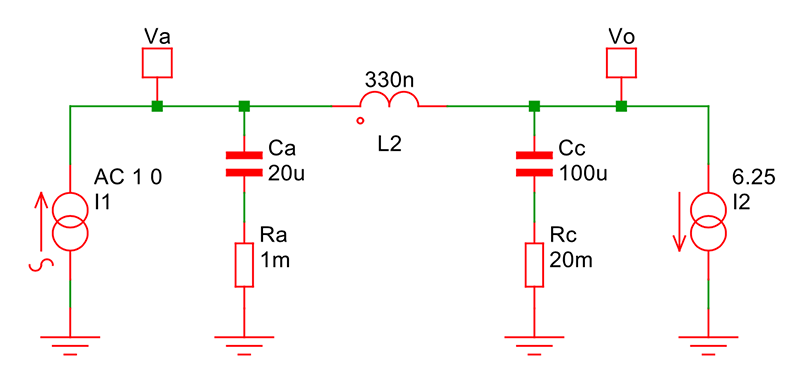
图 3：第二级滤波器可用于阻抗分析
公式 4、5 和 6是各项参数定义：
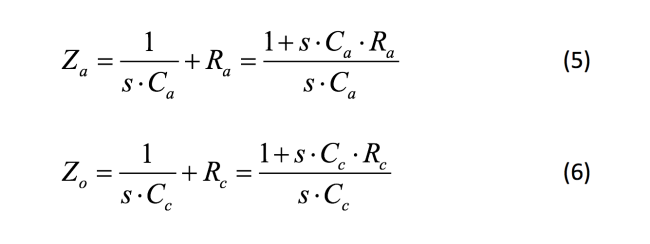
公式7为Va处阻抗的表达式：
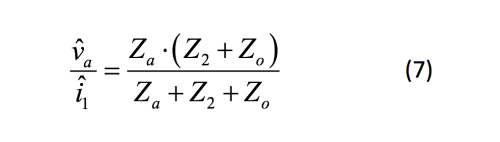
代入各项并简化，形成表达式8：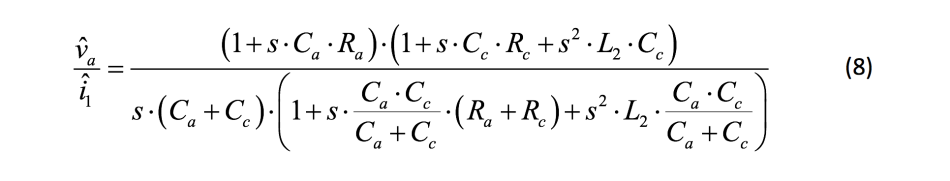
公式9为 Vo处的阻抗表达式：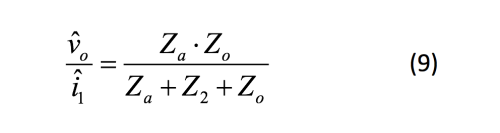
代入各项并简化，形成表达式10：
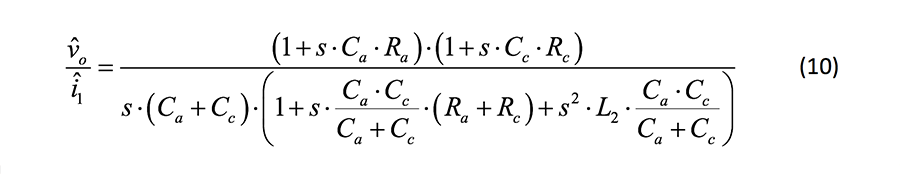以上各表达式中，可以发现分母都是相同的。输出电容有一个主导极点，且第二级电感和串联电容有一个复共轭极点。图 4 清楚地显示了复共轭极点处的共振，及其峰化和相关相移。
Vo处阻抗的增益和相位均符合预期。一个 90 度相移的初始极点，而后跟着一个 180 度相移的复共轭极点。Va处的阻抗表达式的分子中有一个复共轭零点。由于 Cc大于 Ca，因此该零点的出现频率低于复共轭极点。最终的结果会是单极点，但该极点在谐振时明显具有更高的峰值。虚线图表示的是 L2 = 0 时的阻抗。
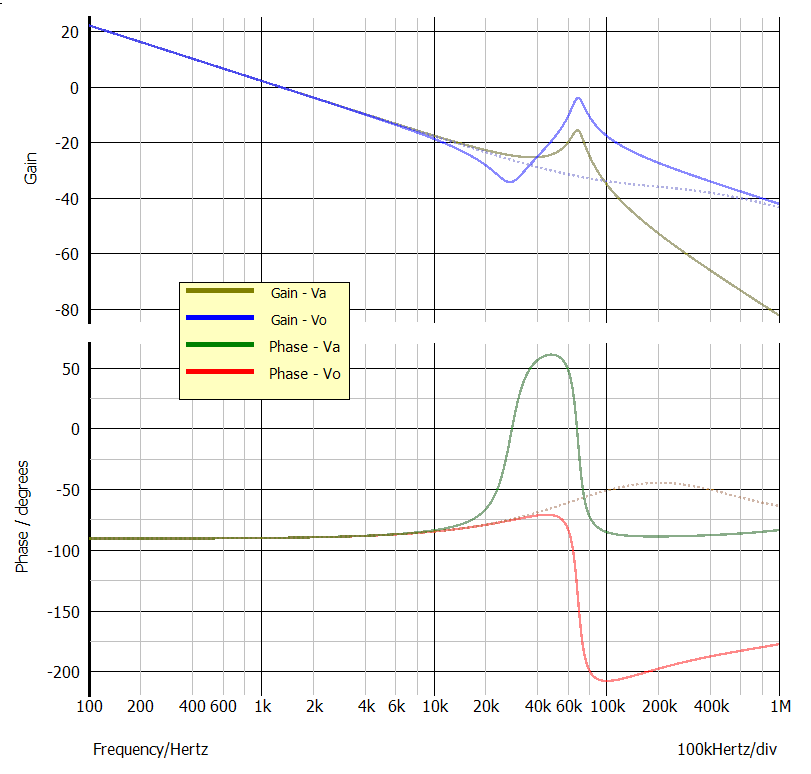图 4：第二级滤波器阻抗图显示了峰值和相关的相移。
那么应该在哪个反馈点处形成闭环控制回路呢？对于有着大量输出电容的负载点转换器，如果第二级滤波器是低电流负载的分支抽头，那么则应考虑在 Va处形成回路。在转折频率远高于控制环路带宽时，则应选择Vo。
您可以从图 5 的图表中观察到，带宽略高于 2 kHz。注意来自第二级滤波器的增益峰值。如果峰值穿过 0 dB 的单位增益轴，则控制环路可能会不稳定，并以谐振频率振荡。
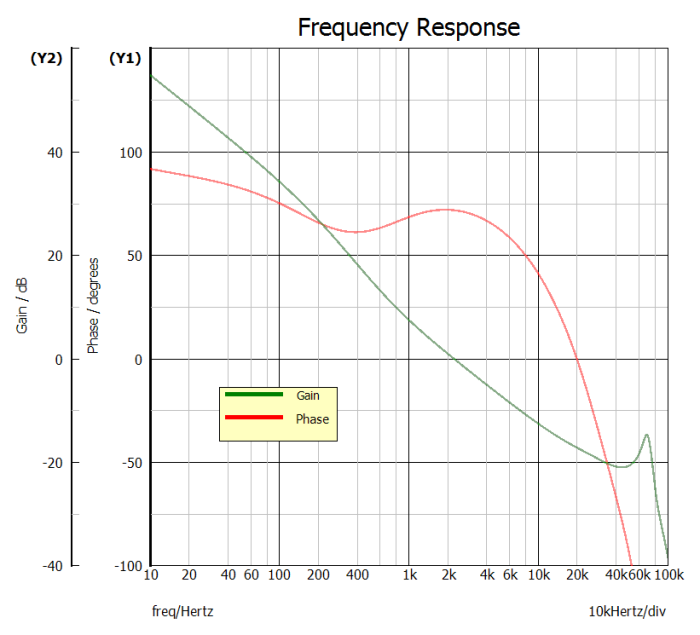图 5：通过频率响应测试可以识别和避免潜在的不稳定性
正如预期的那样，瞬态电压偏差为 1.4V，如图 6 所示。
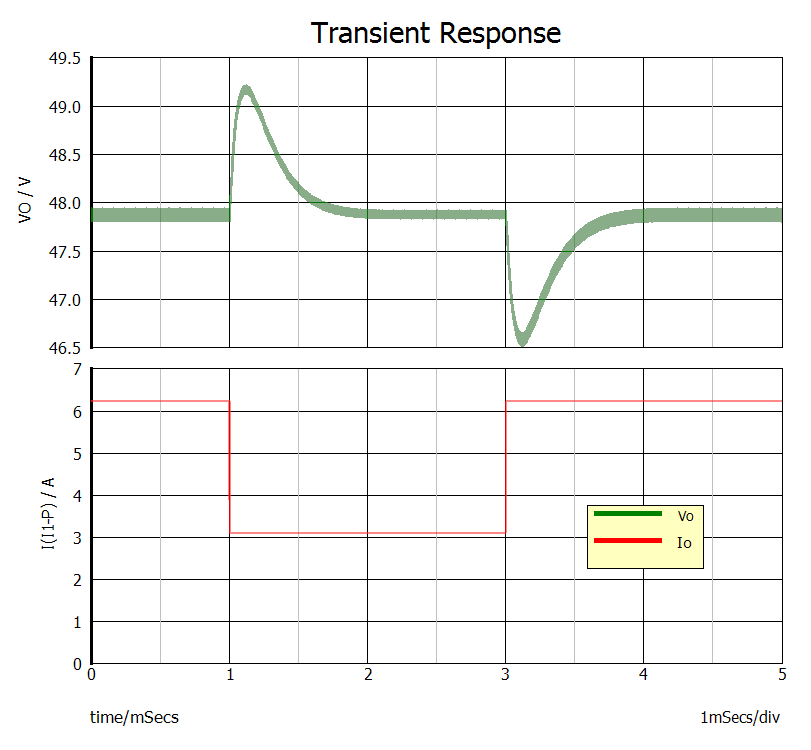图 6：瞬态响应测量还有助于确定可接受的电压范围
模拟图与测试报告中的测量结果一致。由于四相转换器中的末级电容为并联，所以显著降低了实际输出电压纹波。
(参考原文：Meet transient response using a second-stage output filter)
责编：Amy Guan
本文为《电子工程专辑》2021年7月刊杂志文章，版权所有，禁止转载。点击申请免费杂志订阅
您可能感兴趣