控制数字化信号的采样率

数字仪器采样模拟波形并对样本进行处理，以确保数据可以恢复为连续的模拟形式。采样定理表明，信号数字化的均匀采样频率若大于最高频率分量的两倍，信号就可以无误差地恢复或重建。但是，你知道还可以改变数字化数据的采样率吗？

抽取和插值

处理数字化数据的两个最有用工具是抽取（decimation）和插值（interpolation）的数学函数，这些可能是某些示波器上的可选数学函数。抽取也称为稀疏（sparsing）或下采样（down sampling），用于降低数据被数字化的有效采样率。插值或上采样可以有效地提升采样率。

图1提供了两种处理的示例。将10MHz波形以100MSample /秒进行数字化，可得到10个采样/周期（中心左侧网格）。在原始波形的右侧是波形的水平扩展或缩放，将数字化采样显示为波形轨迹上的点。左上角的波形显示了2：1抽取的效果，相关的缩放曲线（右上角）清晰地显示了现在每个周期只有5个点的波形。左下角的曲线显示了2：1插值的效果，右下角是缩放曲线。

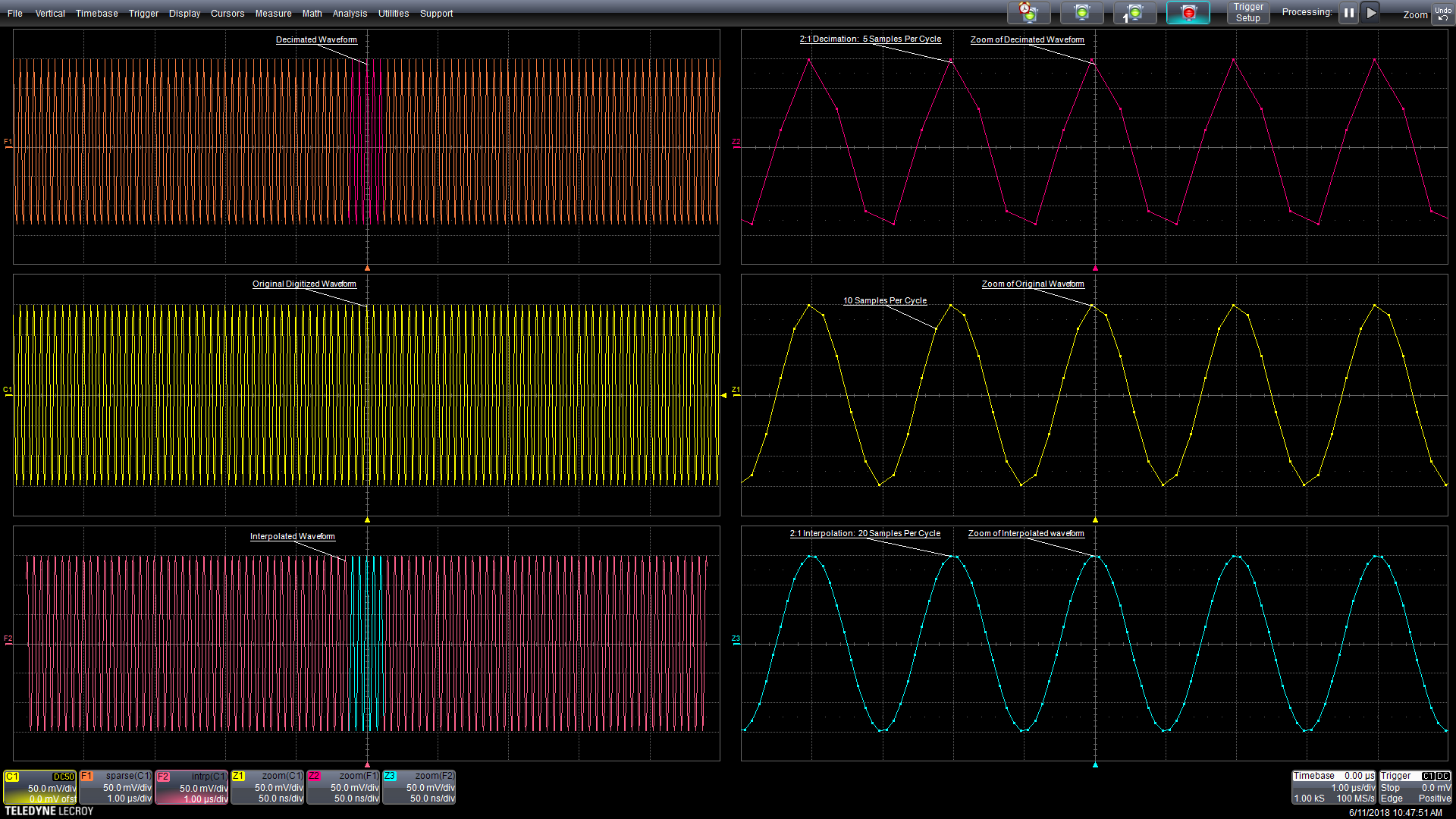
图1：抽取和插值一个数字化波形的详细时域效应。中心迹线是原始波形。顶部曲线显示2：1抽取的效果。底部曲线显示了2：1插值的效果。

在运行任一操作时都必须小心，以确保满足奈奎斯特采样标准，即采样频率大于波形内最高频率的两倍。在抽取的情况下，最终采样率必须大于信号最高频率分量的两倍。同样，在应用插值之前，原始数字化信号必须满足这一标准。

抽取和插值的应用

大多数字示波器（DSO）都有插值的应用示例。它们对采集的样本应用Sin(x)/x插值处理以“平滑”波形，如图2所示。

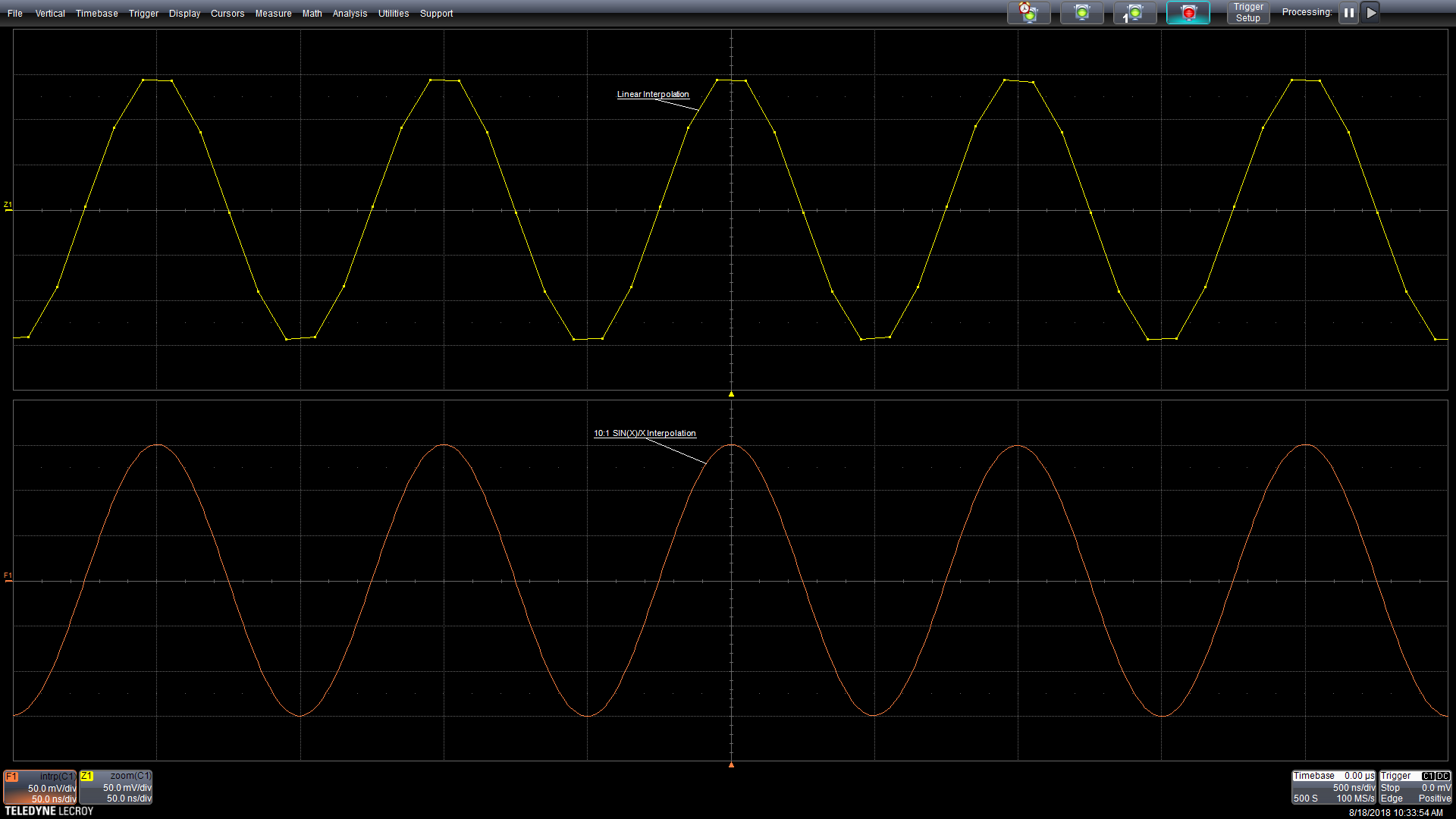
图2：Sin(x)/x插值增加了所采集波形的采样数，并在视觉上平滑了采集的信号。

图2中的顶部曲线是采用线性插值显示的采集波形，看上去基本上是波形的“连接点”视图。亮点表示真实样本的位置。对波形应用Sin(x)/x插值处理，结果波形显示在下部迹线中。该示波器执行10：1插值处理，因此下部迹线中的采样数量是10倍。结果是波形看起来更平滑。请记住，只有在满足奈奎斯特抽样标准时才会出现这种情况。稍后会详细介绍。

抽取最明显的用途是减小数字化波形的大小。抽取通过减少波形中的采样数来节省存储空间并加速信号处理。另一个用途是执行多速率滤波。数字滤波器的频带边缘频率范围是信号有效采样率的函数。要将数字滤波器的截止频率降低到更有用的值，就必须降低有效采样率。

在示波器中有两种方法可以实现这一点。首先是减少采集存储器的长度。第二种方法是使用稀疏或抽取函数来抽取数据。降低采样率会增加数据混叠（aliasing）的可能性，尤其是在捕获富含谐波的信号时。为了限制混叠的可能性，可以高速率对数据进行采样以防止混叠，然后在抽取之前使用数字滤波器进行低通滤波。在对数据执行另一滤波操作之前的这种滤波和抽取的组合被称为“多级，多速率”数字滤波。它能够以最小的混叠风险降低有效采样率，图3示出了一个例子。

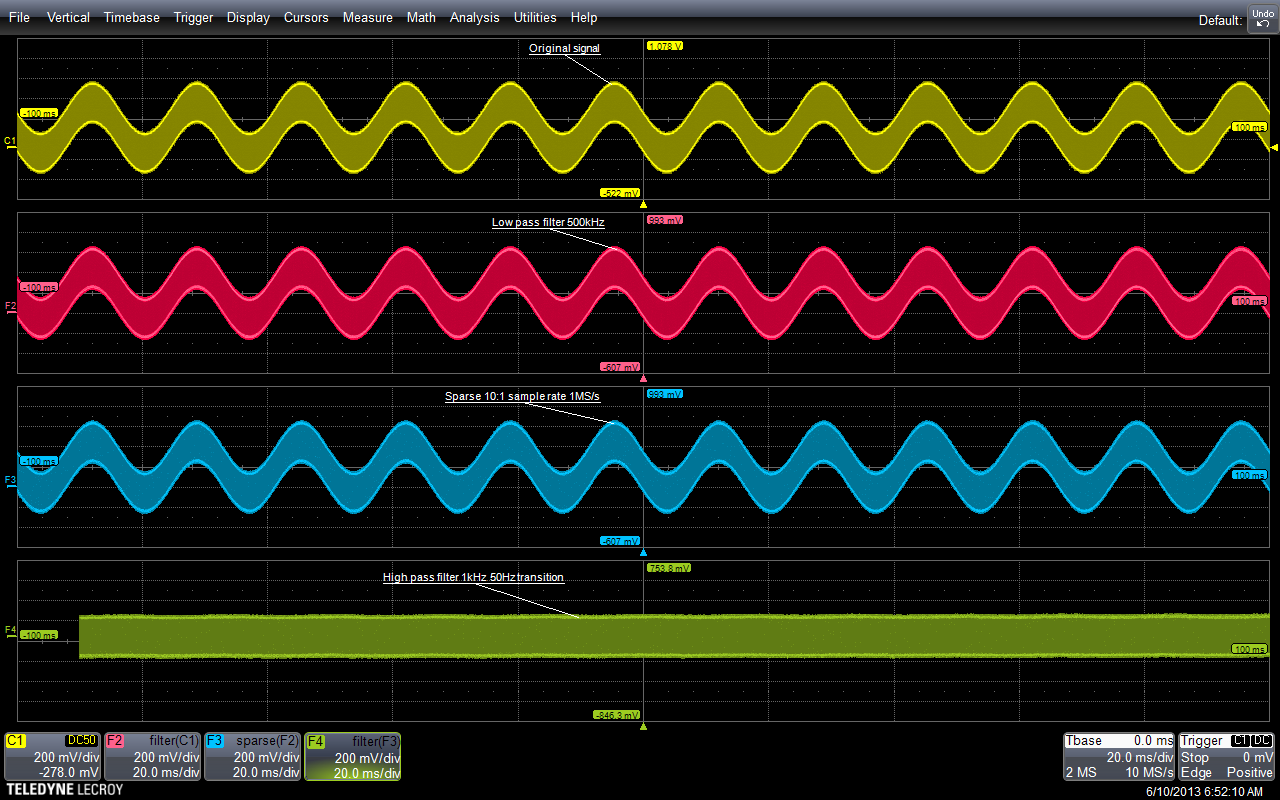
图3：用于实现多级、多速率数字滤波器的数学运算系列，可消除63 kHz信号中的60 Hz分量。

这种类型的信号在开关电源测量中很常见。要测量的波形包含一个63 kHz脉宽调制信号，位于60 Hz正弦波之上。要去除60 Hz分量，需要高通滤波器，而且其通带边缘要高于60 Hz。这种滤波器可以使用有限脉冲响应（FIR）数字滤波器来实现这种类型的滤波器。在采样率为10 MSample / s的信号上使用此滤波器将需要具有大量抽头的滤波器，导致计算缓慢。为了将所需的滤波器抽头数量减少到更有用的值，可以使用模拟滤波、抽取和数字滤波的组合来降低有效采样率。图3中的上部曲线是以10 MSamples/s采样的采集波形。目标是以10：1的比例降低采样率，你可以首先对采集的数据进行低通滤波来实现，其带宽小于所需有效采样率1 MSample/s的1/2。

从顶部开始第二个数学曲线F2，是经过带宽为500 kHz的低通滤波后的信号。第三个数学曲线F3，应用了10：1抽取函数，所得到的抽取将有效采样率降低到1 MSample/s。

数学曲线F4（底部曲线）是高通滤波器的设置。截止频率为200 Hz，过渡区宽度为50 Hz。请注意，滤波过程已经显著降低了60 Hz分量，不再可见了。

抽取扩大了用于移除60 Hz分量的数字滤波器的范围。

测量插值

插值用于增加数字化波形中的采样数。在数字示波器中，它以多种方式使用。最明显的是平滑所显示的波形。所有DSO都能够执行sin(x)/x或线性插值处理，以便在波形中插入额外的点，使其看起来更加连续，如前所示。

在测量期间内部也可以使用插值来更精确地定位测量阈值交叉，使之比采样周期间隔更好。它通常作为独立的可选数学函数提供，可让用户对所采集的波形执行特殊处理。

通过在特定级别找到波形的交叉点可以执行示波器的时序测量。在许多情况下，信号的上升时间非常快，对于20 GHz的采样率，边缘上只有少量采样。简单地在阈值周围的采样之间画一条线是找到交叉点的最直接的选择。然而，当采样在阈值的两侧不对称地间隔分布时，这会导致较大的误差。为了避免这个问题，DSO使用三次插值来填充所采集的样本，并且通过阈值两侧的两个插值抽样之间的线性插值来找到交叉时间，如图4所示。三次插值可提高计算效率，提供准确的采样插入，而且计算速度比sin(x)/x插值更高。

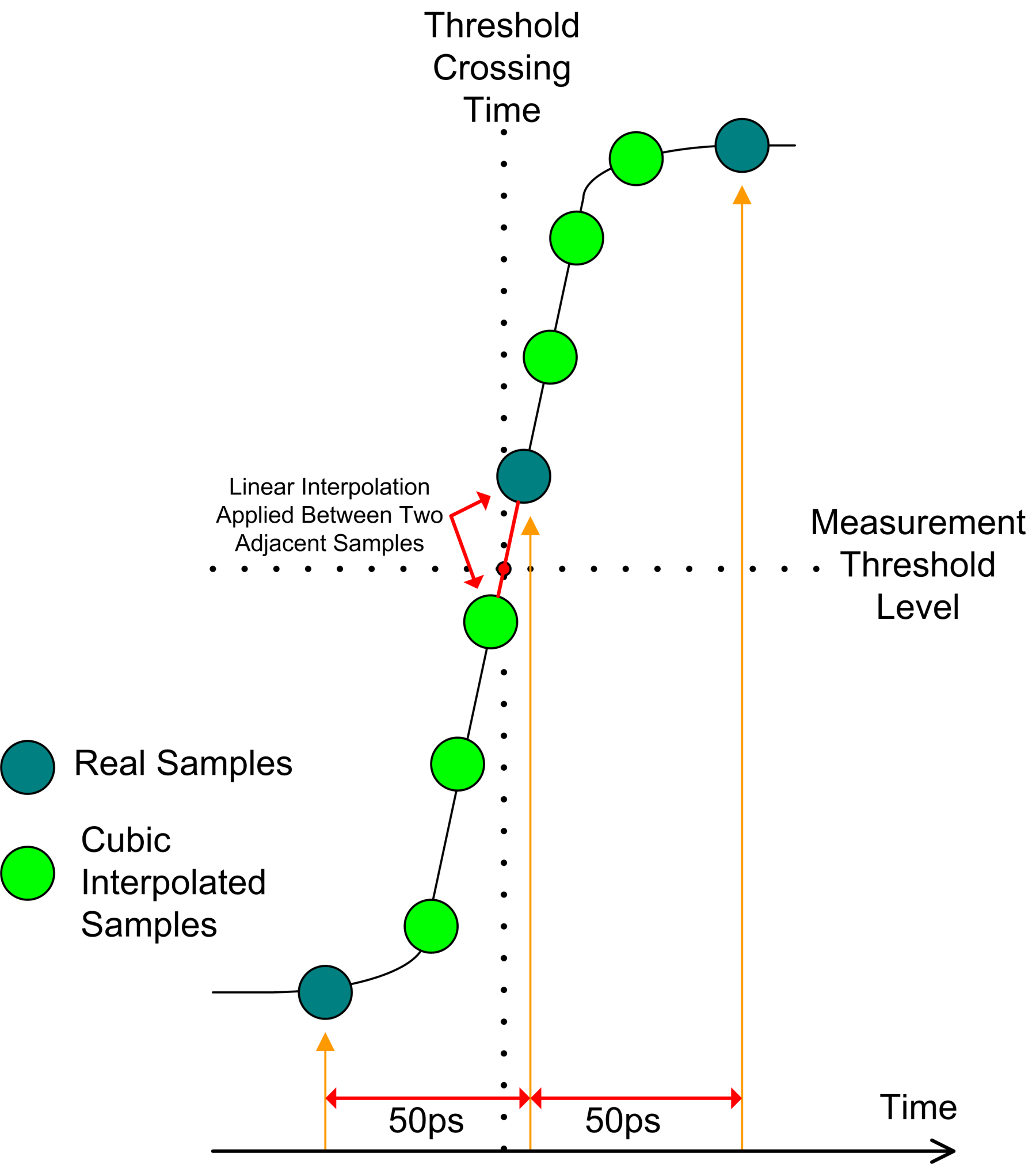
图4：内部DSO测量使用三次插值与线性插值相结合的方式来提高测量的时序分辨率。

Threshold crossing time：过阈时间

Linear interpolation applied between two adjacentsamples：在两个相邻采样之间应用线性插值

measurement threshold level：测量阈值水平

Real samples：真实采样

Cubic interpolated samples：三次插值采样

在波形振幅超过预定阈值的点测量时间。该示例的采样间隔为50ps，20GSamples/s。对波形应用三次插值，然后对最接近交叉处的点进行线性插值，以找到阈值交叉的确切时间。所得测量值的时间分辨率比以采样周期为间隔的原始采样高得多。

什么可能出错？

稀疏最常见的问题是抽取波形采样，直到不再满足奈奎斯特标准。所得到的波形将明显失真，并且在视觉上易于识别。但是，如果通过计算机解释波形，结果可能是灾难性的。

插值引起的错误更加微妙。考虑将插值应用于方波的情形，如图5所示。

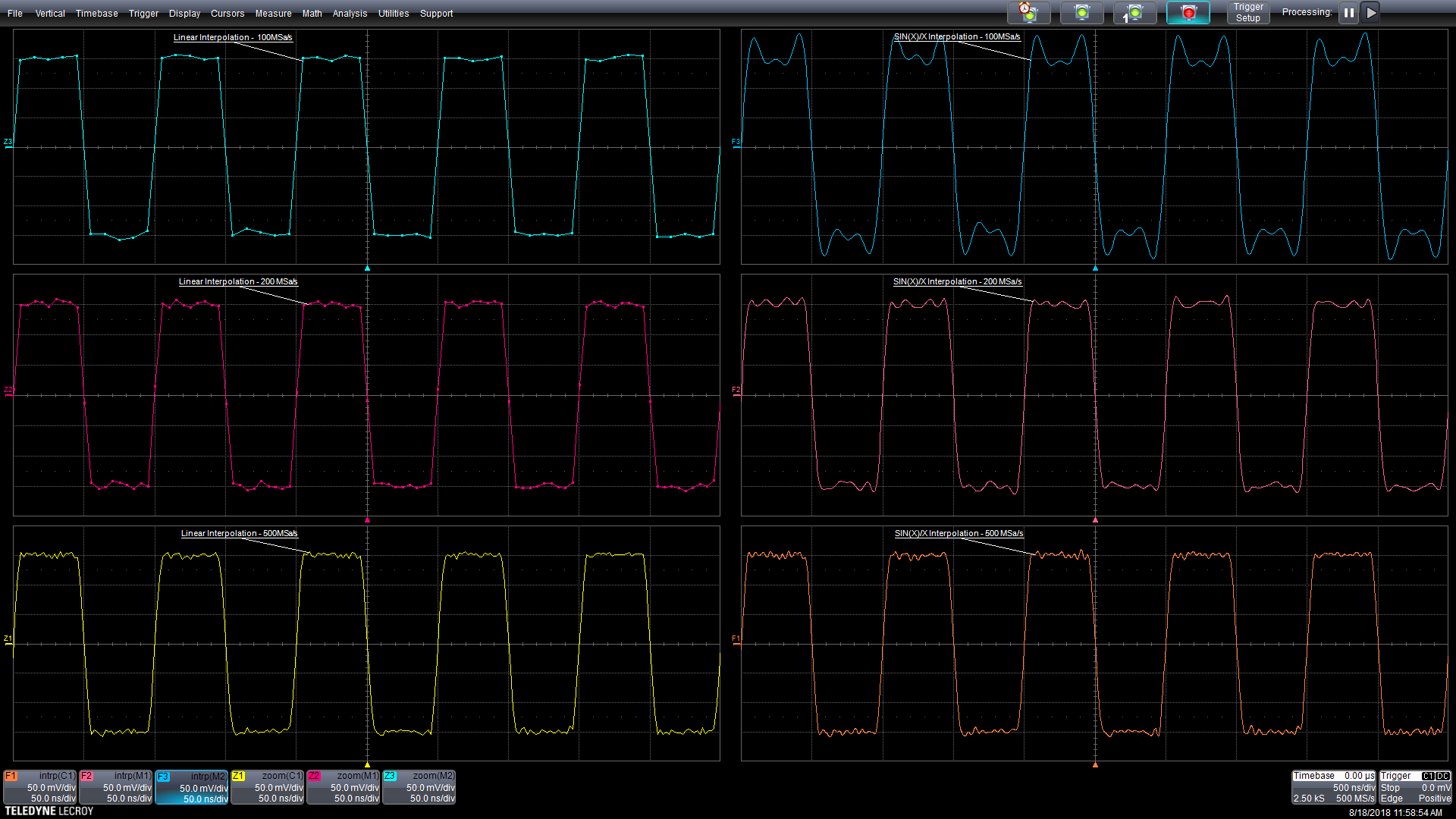
图5：当使用抽取时由欠采样引起的Sin(x)/x插值错误的示例。

方波的频率为10 MHz。在底部迹线中，它以500MSa/s或50倍过采样的方式采样，每个周期有50个采样。左侧迹线使用线性插值，右侧的使用sin(x)/x插值。使用两种不同插值的波形几乎没有差别。

中心迹线的采样为200 MSamples/s，或20个采样/周期。请注意，线性插值波形的边缘只有一个采样。两种波形看起来略有不同。

顶部的迹线对以100 MSa/s采样，每周期10个采样，而边缘没有采样。边缘的转换时间等于或低于采样周期。此时，Sin(x)/x 插值显示不存在的过冲（overshoot）和预拍（pre-shoot）。这种现象被称为吉布斯耳朵（Gibbs ears）。

出现吉布斯现象是因为方波的频谱具有许多奇次谐波。大多数工程师估计带宽包括高达五次谐波，在这种情况下为50 MHz。波形处于混叠的最边缘，这会损害Sin(x)/x插值。在切换到Sin(x)/x之前，最好使用线性插值来查看数字波形，以避免对不存在的过冲造成不必要的恐慌。

结语

插值和抽取是很有用的示波器数学函数。显示和测量插值通常包含在DSO中，而独立数学函数也可能是可选的功能。增加或减少有效采样率的能力有可能是其它更高级功能（如滤波）中最有用的中间步骤。其它功能还包括相对于波形移动采样位置的能力。