未来的电动车充电站需要配置多少充电器以及需要多快的时间充满电，才能达到让使用者可接受的最少等待时间？
最近，气象预报员高度肯定地预期在我们居住的地区会有一场大雪/冰风暴。我赶在暴风雨来临之前外出办点事情时，碰巧经过一座有着12台加油机的加油站，几乎每一台机器前都排了三、四辆车等着加油。尽管队伍很长，但它的移动速度很快，每辆车只需要不到五分钟的时间就加好油了，所以等待时间是可以接受的。
这让我联想到如果相同的情况发生在电动车(EV)呢？无论您对于EV是否可行或可取的看法如何——这又是另一个话题了——事实是要让EV充满电所花的时间比起为汽油或其他碳氢化合物驱动的车辆加满燃料的时间更长。根据充电设置等级和电池容量(参见下表)的不同，大约需要花费1～10个小时以上的时间。可以确定的是这一定会让EV充电站大排长龙且移动速度缓慢，再加上许多暴怒的驾驶人。值得注意的是，EV充电着重的是每分钟跑多少公里的续航力指标，而不再是加了多少升的汽油。
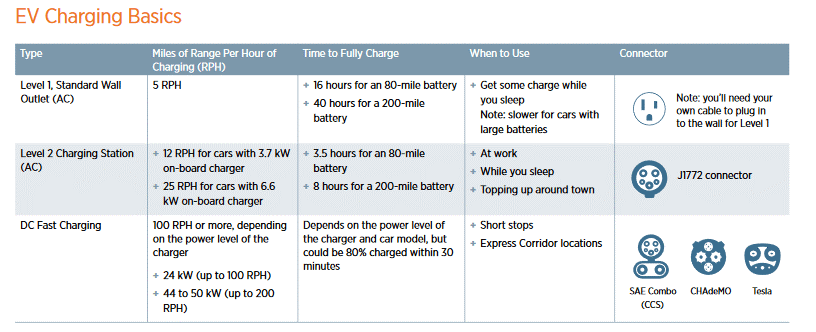
电动车充电选项摘要提供了初步指南，此外还有许多其他因素需要考虑（来源：Electronic Products/AspenCore）
广义的来看EV充电的情况，在许多方面，它类似于生活中面对许多方面的问题：您需要多少“server”(服务)来支持预期的使用需求(此处的server指的是服务的人员与设备，而非数据中心服务器)。这的问题也适用于零售商店、各种电话求助专线、医疗设施、因特网/网络服务器等问题。早期针对基本电话业务通常进行早期了详细的研究和分析(例如贝尔实验室)，从一个名为“Erlangs”(话务量电话流量单位)的测量参数开始，将电话电路上的总通话流量进行了量化(而且还有Erlang B和Erlang C等版本)。
如今，随着分组交换电话成为主流以及电路交换线路逐渐消失，您不会再听到太多关于Erlang和话务量与分析的消息了。然而，这个术语的使用频率曾经一度与每秒兆位(Mb)一样频繁。与Erlang相关的研究采取不同的观点来回答这一类的问题：对于特定数量的Erlang，局端(CO)需要多少线路接口单元(LIU)才足以提供所需的服务水平？在此队列分析中存在很多变量，其中包括：
• 理想的服务等级是什么？如果必须让用户等待，问题可能是“有多少LIU可确保95%的用户等待时间不到一秒钟？”
• 对于具有定义均值的特定随机呼叫/时间段，应该使用哪一种通话概率分布(一般经常使用的是Poisson分布)？
• 同样地，如果通话的时间长度是随机的，那么具有特定平均值的随机概率分布为何？
• 最后，在此假设下，用户接取至LIU的最长等待时间是多少？
电话系统工程师采用这些与参数相关的变量进行模拟，就可以放心地回答问题，例如“支持10,000个电路的局端需要多少LIU，才能确保95%的通话者等待不到1秒钟就能连接到LIU？”连接局端的主要线路也进行了类似的分析。
当然，在预测的峰值事件出现时，这一分析就变得更加复杂了。据说母亲节是通话量最高的日子，通常发生在下午12点到6点之间。因此，在分析时会遇到正常峰值流量负荷以及不寻常的峰值等问题，以及如何调整资源大小以因应所需的性能水平。简言之：它会变得更复杂，这是肯定的。
EV充电的情况也是一样的。先从一个“正常”的情况来思考可能会好一点，毕竟，如果家家户户都有一辆EV并且可在自家过夜充电，但现实上根本不可能。因为许多车辆并不会安装个别充电器(有些车子甚至停放在街道上)，那么究竟需要多少公共充电站？这显然取决于许多因素的机率统计。
当诸如预测风暴出现的事件时，还可能发生峰值对峰值负载(peak-peak load)的问题。那么，所有这些正常的队列假设都是无效的，而且必须转到另一种分析模式——其结果将大不相同。如同所有流量和需求情况一样，等待时间太久之后就会出现一个爆发点，因为每次只有一个用户可以使用该系统(当然，车辆的交通流量也发生相同的情况)。
当然，对于EV来说，重要的不只是充电站的数量、用户需求和充电时间。互补的问题也很重要：地区“电网”是否提供足够的峰值功率以及在何种程度上将成为限制峰值服务的因素。就像大多数加油站提供10,000加仑的大油箱一样，也许未来的EV充电站将拥有大型的现场电池组，平时用于为EV电池充电，并在繁忙时段释放能量。还有一些超高功率充电站也正展开工作，例如西门子(Siemens)和BMW主导的FastCharge联盟以及其他计划。该联盟在去年12月展示175kW和450kW的EV充电速率，只消不到3分钟的充电时间就达到了100公里的续航力，完全充饱电则约15分钟。这或许有助于解决充电时间的问题，但对于电网来说却是很大的功耗。
西门子和BMW主导的联盟开发出FastCharge EV充电系统，并展示了175kW和450kW的EV充电速率（来源：Siemens）
您认为在什么样的情况下，充电站数量和等待时间会成为EV的重大问题？你想到了什么解决之道吗？您认为在过个5年、10年和20年之后会发生什么事？
编译：Susan Hong EETTAIWAN
- 这方面有专门的数学理论和工具——排队论。
您可能感兴趣
