解析功率传输和相位基础关系

本文讨论电气工程的基本原理，并试图梳理出一些新的见解。对许多人来说，这会是早已知道(或曾经知道)的概念所作的一个更新，但笔者会尝试在论述中添加一些新东西。

雅可比定律(Jacobi's Law)

大多数工程师都熟悉最大功率传输定理(也称为雅可比定律)。图1显示了一个电阻源和阻性负载，其目的是将功率从电阻源传输到负载。这个原理可以如此阐述：“当电阻源的内阻等于负载的电阻，所传递的功率最大，外部电阻可以改变，但内部电阻是恒定的。”(图1)。

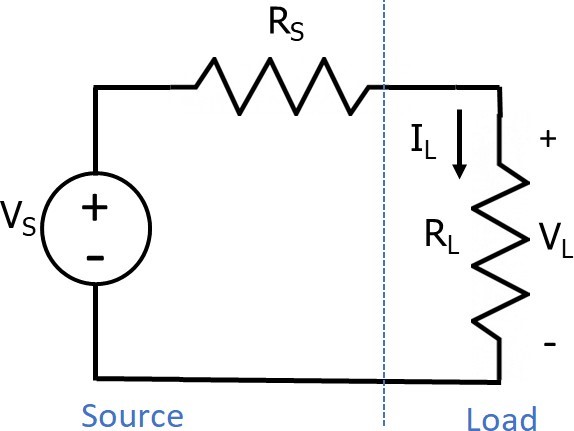
图1 电路图显示连接到阻性负载的电阻源。

当RL = RS时，传输到负载的功率最大。一个经常被忽视的约束是假设源电阻(RS)是固定的，不受控制，否则，会选择RS = 0作为从电阻源获得最大传输功率的最佳值。

图2显示传输给负载的功率如何随RL / RS变化。传输到RL的功率取决于通过负载的电流和负载两端的电压。RL值变大会增加电压(VL)，但使电流(IL)减少，类似地，RL值变小会增加负载电流，但会降低负载电压。运用一点微积分知识可以看出，最大功率发生在RL = RS时。

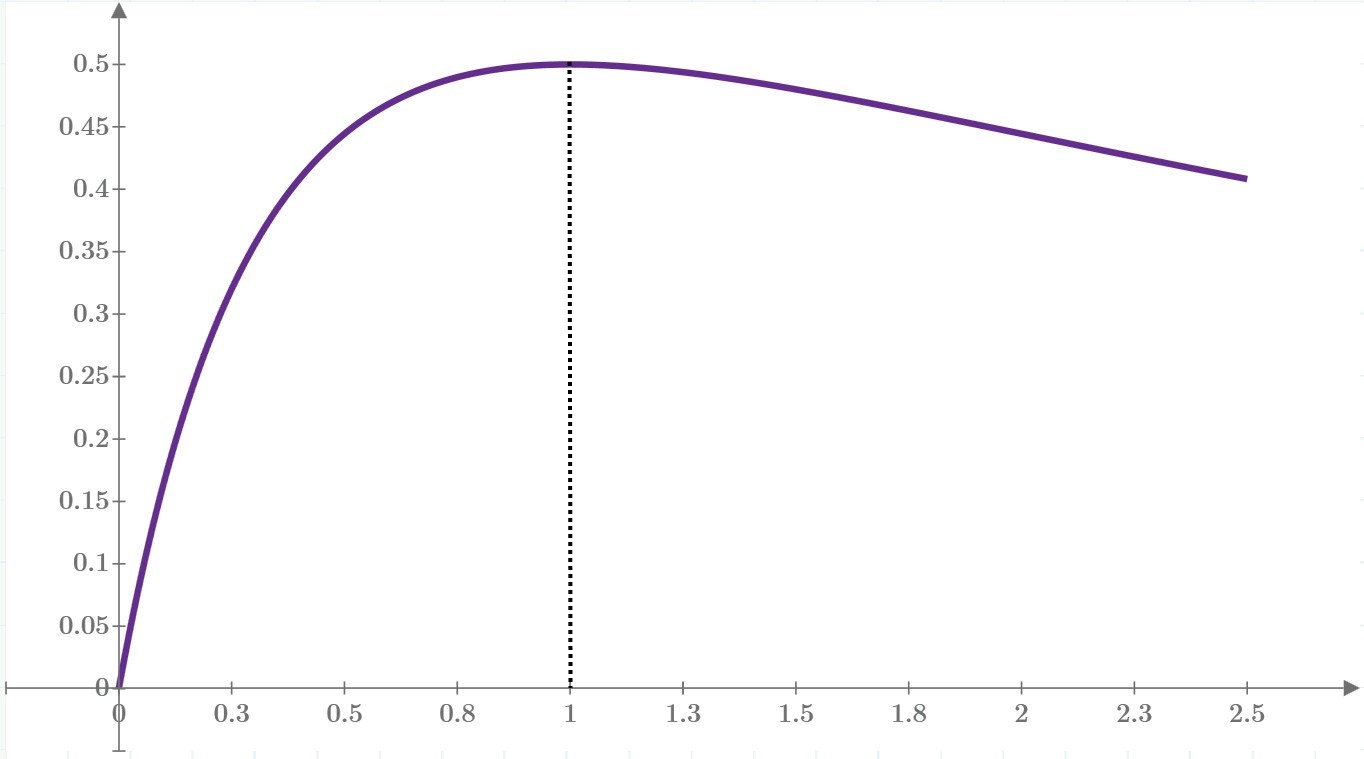
图2 PL与RL / RS的关系曲线显示，当RL / RS = 1时负载的功率最大。

复阻抗

现在考虑阻抗是复数的AC情况，如图3所示。源阻抗为ZS = RS + jXS，负载阻抗为ZL = RL + jXL，当ZL是ZS的复共轭时，产生最大功率传输。也就是说，RL = RS和XL = -XS，这有时被称为复共轭匹配，正如预想的那样，如果XS = 0，又退回到阻性的情况。

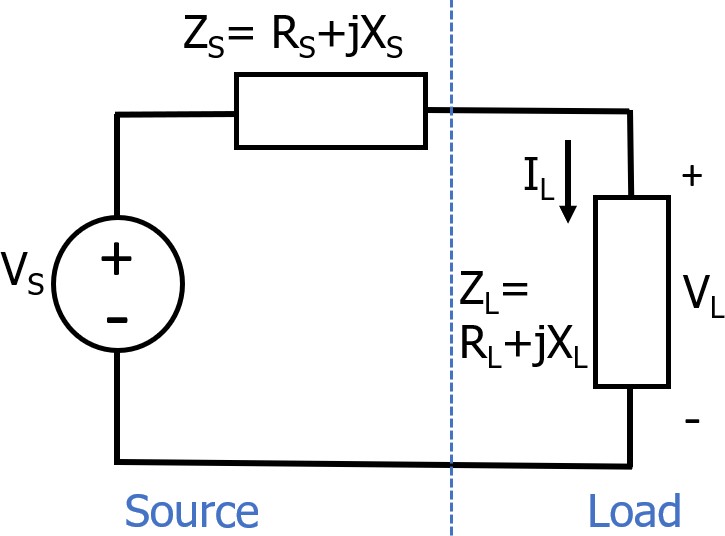
图3 电路图显示相连的负载和电源都有复阻抗。

都与相位有关

有趣的是，当XL = -XS时，电压源VS可看做纯电阻(RS + RL)，这显示电压源输出的电流与电压同相。这并非巧合，电压和电流波形之间的相位在负载的平均功率中起着重要作用。来看看复阻抗的瞬时电压、电流和功率的时域表示。
瞬时功率由公式(1)给出：

p(t) = v(t)i(t) (1)

假设v(t)和i(t)都是正弦曲线：

其中Φ是电压和电流波形之间的相位差。

图4显示了在Φ=45°时的时域波形v(t)、i(t)和p(t)。

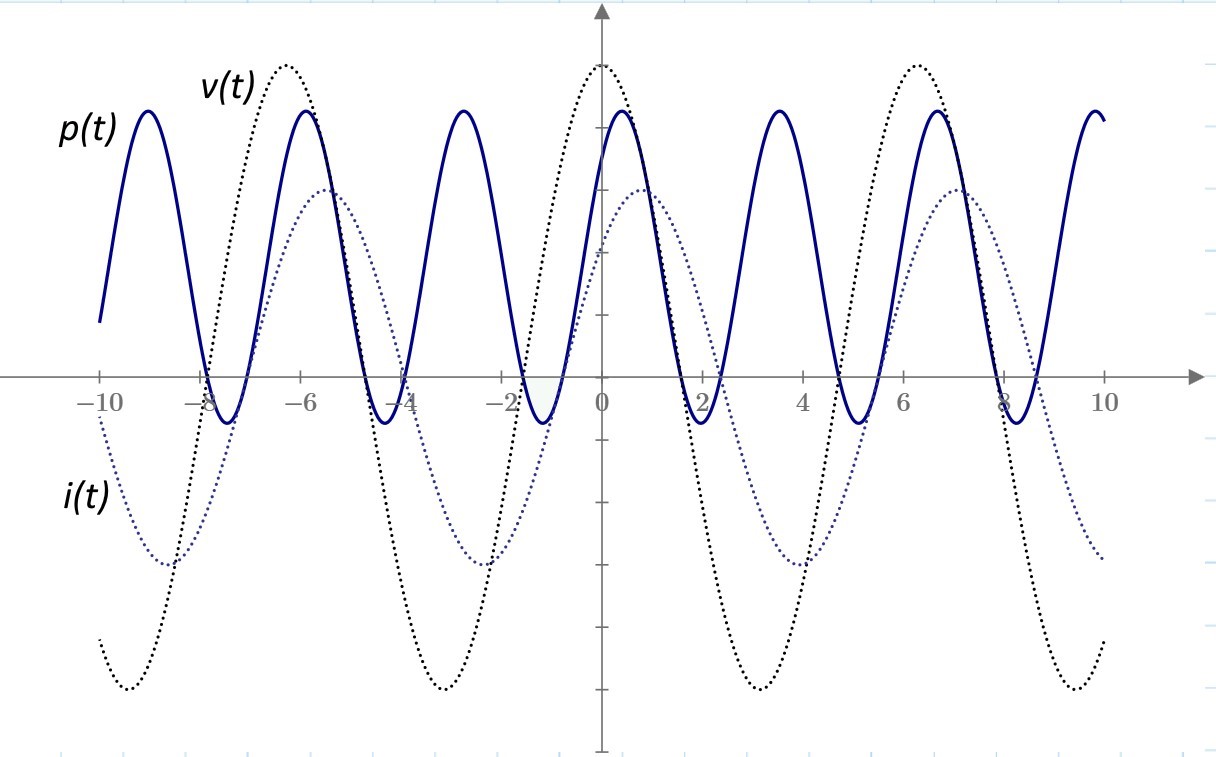
图4 Φ=45时的v(t)、i(t)和p(t)波形图。

应用三角函数恒等式：

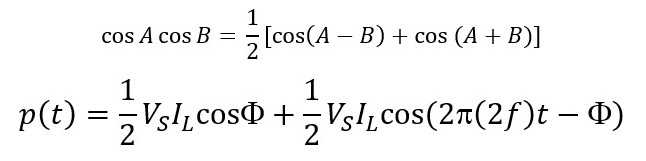
p(t)表达式由常数项(1/2VSILcosΦ)和两倍于原始频率的余弦函数组成。我们通常只对波形中的平均功率感兴趣，这可以透过在波形的一个周期上对p(t)求积分得到。双频余弦将平均为零，仅留下常数项，因此平均功率为：

PAVERAGE = 1/2VSILcosΦ。

图4中的p(t)曲线说明，瞬时功率以正弦方式变化，甚至在部分周期内变为负值。只要Φ不等于零，都有可能发生这种情况。从图中还可以看到，p(t)的平均值为正，这表示功率被传输到了负载。

电力工程师会使用真实功率和视在功率(Apparent Power)的概念来量化相位对功率的影响。真实功率代表实际传输的功率，包括v和i之间的相位影响，以瓦特(W)为单位测量。视在功率是一个更简化的概念，只是原始电流乘以电压，以伏安(VA)为单位测量，以区别于真实功率。

电力工程师也使用功率因子(PF)的概念：

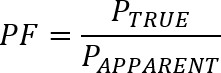
对于正弦波形，功率因素等于电压和电流波形间相角的余弦：

PF = cosφ

功率因子是量化有多少视在功率转换为有用(真实)功率的简单直觉方式。如果Φ=0，则PTRUE = PAPPARENT，PF=1；当Φ=±90°时，PTRUE下降到零，PF=0。图4所示的例子是Φ=45°，功率因素=0.707，说明PTRUE等于PAPPARENT的70%。

总结

本文回顾了最大功率传输的基础知识和相位关系的重要性，并将其与功率因子、真实和视在功率等电力工程概念结合。笔者故意忽略了对传输线的讨论，但这些功率传输概念与通常的传输线概念(例如驻波比、回波损耗和反射系数)有很多共同之处。