神经网络与量子计算：从经典深度学习到变分量子算法

机器学习已经深入了每一个可以想象的领域，从医疗到教育，从金融到军事，从营销到农业。这意味着这些ML算法的复杂性正在呈指数级增长，因此，由于其参数数量巨大，使得它们越来越难以训练和微调。

由于量子计算机能够同时计算大量的状态，并且有能力将任务并行化，因此使用量子计算机就不存在这个问题了。这些计算机使用了量子物理学的特性：叠加、干涉和纠缠。

为了理解量子机器学习和量子神经网络，可以从理解经典深度学习的工作原理开始。

经典深度学习

深度学习是用可组合的可微函数构建机器学习模型。

经典的深度学习包括以下内容：

构建具有可训练参数的神经网络。

定义成本函数。

梯度下降：1. 计算成本 wrt 参数的梯度。2. 更新梯度方向的参数。3. 重复直到找到最小损失。

训练后，模型可用于分类、预测等。

深度学习领域开辟了可微分编程的新领域。可微分编程说任何代码都应该是可训练的，而不仅仅是机器学习模型。

量子计算

量子计算是一种独特的计算范式。量子系统是通过量子电路中的一系列量子门来操纵的。

量子电路是可微的（即量子电路的参数可以改变）。因此，这里可以应用可微编程的思想！

因此，量子电路可以像神经网络一样进行训练。

这称为量子机器学习。

量子机器学习模型的训练将比标准机器学习模型快得多，从而使我们能够训练具有大量时期、更密集层和更多参数的模型。

变分量子算法

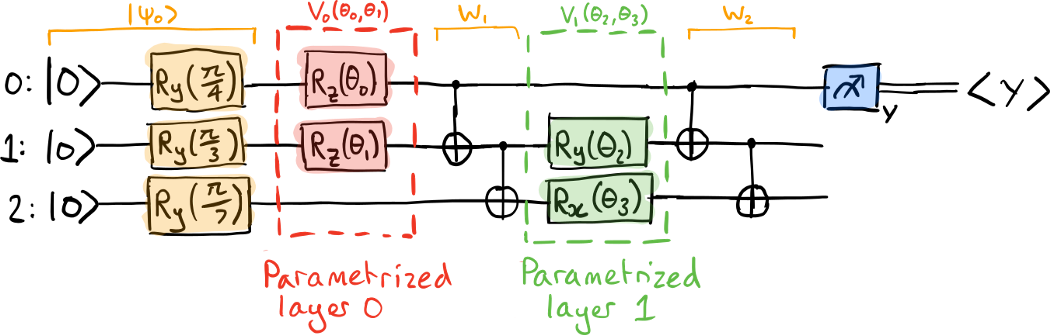
变分量子算法是“像训练神经网络一样训练量子计算机！”这一理念的实际体现。

变分量子算法电路由以下部分组成：

准备一些初始状态|ψ⟩。

使用一系列门执行一些参数化的酉变换 U(θ)

测量可观察的属性作为输出。

量子神经网络 (QNN) 的结构类似于经典神经网络。

QNN 由以下部分组成：

电路架构也称为ansatz。

特定于问题的成本函数。

一种训练算法（例如梯度下降）。

变分量子算法在各个领域都有应用，包括从药物发现到投资组合优化。