新能源电动汽车已经成为世界各国最重要的战略领域，电动汽车与传统汽车的不同之处不仅仅是从燃油过渡到新能源，另一方面动力系统也从燃油发动机过渡到电机电动驱动，这其中就涉及到最基本的电动力学问题。本文对电动力学的基础问题进行介绍，其中的精髓是：使用对称性极大地简化了难懂的场论。
新能源电动汽车已经成为世界各国最重要的战略领域，电动汽车与传统汽车的不同之处不仅仅是从燃油过渡到新能源，另一方面动力系统也从燃油发动机过渡到电机电动驱动，这其中就涉及到最基本的电动力学问题。本文对电动力学的基础问题进行介绍，其中的精髓是：使用对称性可以极大地简化难懂的场论。
电动力学
为什么我们关心电动力学？电动力学是研究源自移动电荷的磁场和电场。它对工程到科学仪器的几乎所有事情都很有用。很多人认为这是一门枯燥的学习科目，尤其是把这门课作为选修课的纯数学学生。然而，电动力学也有很多有趣的理论和学术成分。
实际上，一开始电动力学的主要问题是弄清楚当我们在某些位置放置电势时电场和磁场是什么样的。
在这篇文章中，将在处理此类问题时所考虑的事情提供一些观点和方法。
如何开始描绘球壳上的电场是什么样子的？
为了在经典的思维框架中解决这个问题，需要使用高斯定律，这是麦克斯韦方程组的结果之一。具体来说，高斯定律指出，在任何给定点上，电场的发散应该与该点的电荷密度成正比。这显示在下面的等式中，此时，就要弄清楚电场 E 的原理。
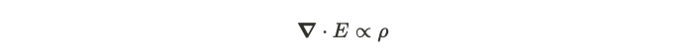
这条定理有什么用处？
我们可以从这个表达式中得出有用的结果，这使我们能够以实际的方式评估 E。当我们在包含电荷的某个表面上积分时，我们使用斯托克定理将体积积分转换为表面积分。当我们使用斯托克斯定理切换到曲面积分时，我们不再需要担心求解微分方程。
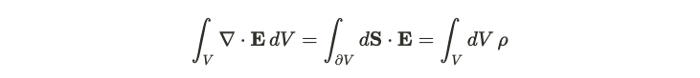
在这种情况下，斯托克定理是微分几何中一般结果的特定情况，其中在体积上积分的形式的外导数与在边界上积分的形式相同。
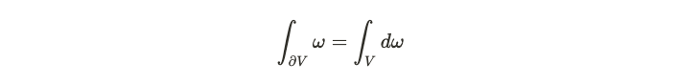
我们需要选择一个表面来约束这个体积。有趣的是，我们选择绑定这个体积的表面并不依赖于表面本身的形状——重要的是我们绑定了电荷。为了解决这些问题，诀窍是使用尊重问题对称性的正确坐标集。如果问题采用球对称形式，我们最好使用球坐标，因为它使表面积分的计算更容易评估。很多时候，这使得 ansatz - 一个猜测 - 更容易想出。在球对称源电荷的情况下，电场只是半径的函数的猜测是完全合理的。
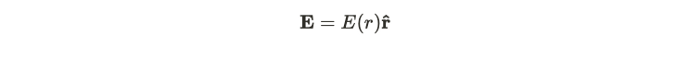
一旦我们想出了这个ansatz，那么计算表面积分就是一件简单的事情。到目前为止，这种方法可以让我们想出一些问题的答案，例如：
- 球壳周围的电场是多少？
- 线周围的电场是多少？
- 点电荷周围的电场是多少？
有一些常见的充电电位会一次又一次地出现。其中之一是单点充电。这是一个看起来像狄拉克δ函数的势能，看起来像这样，以原点为中心。
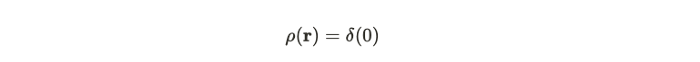
在这里使用的最有用的工具之一是使用对称性的有根据的猜测。它将使用问题的线性来找到解决方案，然后使用唯一性。如果我们有一个看起来很复杂的势能，比如两个点电荷，我们可以通过单独研究每个势能来简化问题，然后将解决方案合并。
参考
[1] Feynman, RP, Sands, M., Leighton, RB (2015)。
您可能感兴趣
