来源 | 工程师看海

智库 | 云脑智库(CloudBrain-TT)

云圈 | 进“云脑智库微信群”,请加微信:15881101905,备注您的研究方向

数字世界是现实世界的镜像，模数转换器ADC则是连接这两个世界的大门。采样速率是ADC重要参数之一，围绕采样速率，有一条著名的定理：奈奎斯特采样定理。

采样定理：

只要采样频率大于或等于有效信号最高频率的两倍，采样值就可以包含原始信号的所有信息，被采样的信号就可以不失真地还原成原始信号。

采样定理是美国电信工程师H.奈奎斯特在1928年提出的，在1948年，信息论的创始人C.E.香农对这一定理加以明确地说明并正式作为定理引用，因此在许多文献中又称为香农采样定理。

为方便介绍，我们统称之为采样定理。

在详细介绍采样定理之前，我们一定要知道一个非常有趣的频率现象：‘任何模拟信号，在离散化后，在频率上都会按照采样率周期性延拓。’

先抛个问题：

我们以fs=100Hz的采样率，采集一段模拟信号，得到了100个采样点，我们能够重构出原始的模拟信号，得到模拟信号的频率信息吗？

理论来讲是不可能的，模拟信号一旦经过采样离散化后，其波形就已经失真了，我们永远无法完美的重构原始模拟信号。

其中一个重要原因是，我们无法区分离散后信号的频率信息。

我们从时域和频域两个方向分别理解：‘我们无法区分离散后信号的频率信息’这句话的意义。

时域解释

下图蓝色点是采集后的一段离散序列，我们无法知道采样的原始信号是红色曲线还是蓝色点直连重构的曲线。

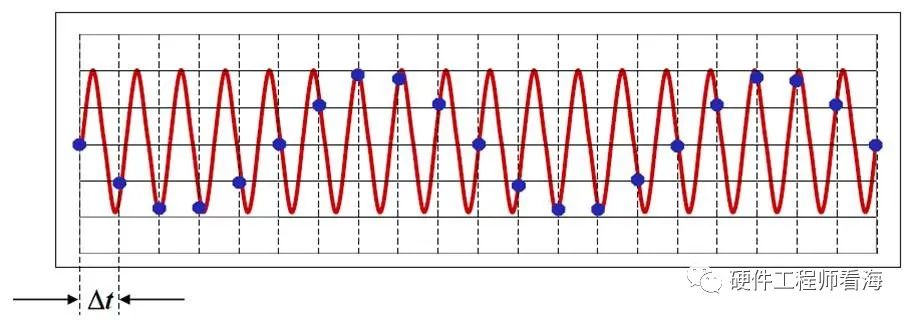
通常情况下，我们重构采集后的离散点方法是直接连接相邻采样点。

基于这样的方法，我们直接重构后的最低频率为fa，而理论上可以提取出（fa+n*fs）Hz的信号（n为≥0的整数，fa为原始信号频率，fs为采样频率）。

比如一段频率为fa=10Hz的模拟信号，经过采样频率fs=100Hz后，离散后的信号可以重构为10Hz、110Hz、210Hz。这个特性就是信号频率的模糊性。

频域解释

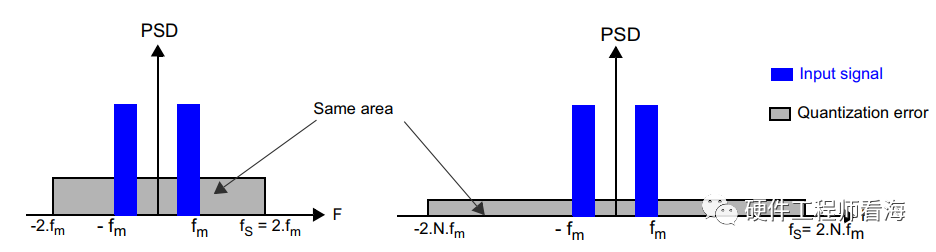
一段频率为带限为fa的模拟信号，经过采样频率fs采样后，其在频谱上的波形会按照fs周期性复现，波形见下图。

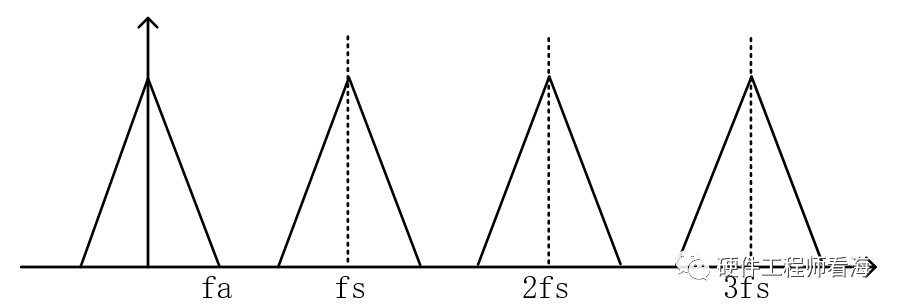
这是一个非常有趣的现象，可以看到时域的结果和频域的分析是统一的。

而这里面就隐含着著名的采样定理。

同样的，我们从时域和频域分别看下采样定理的理解。

时域分析

在时域的角度下，当一个周期采集点数少于2个时，我们直连采样点重构信号，则频率就错了；而当一个周期采集两个采样点时，采用直连的重构方式，我们起码可以得到原始信号的频率信息。

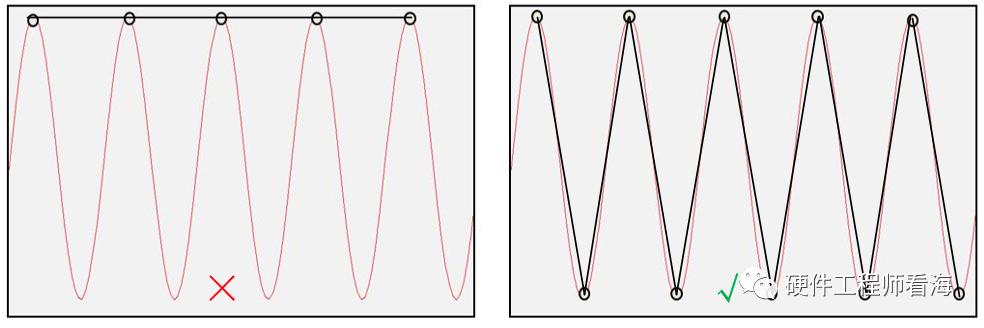
频域解释

如下图所示，当fs<2fa时，周期性复现的带限信号，会有红色重叠的地方，这会导致我们失去原始带限信号的基本频率信息，俗称频谱混叠。

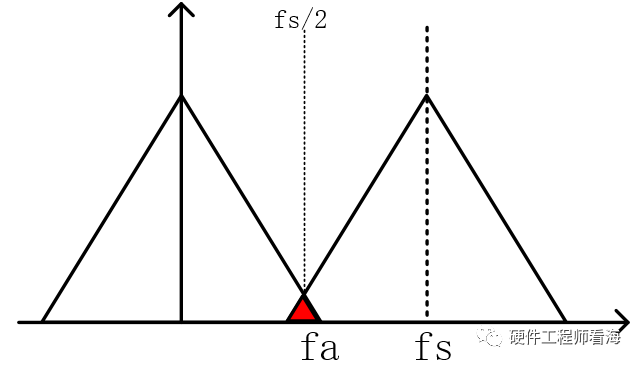
如上就可以提炼出采样定理的基本要义了。

采样定理与过采样率

上文中的fa是信号的带限（信号的最大频率范围），2*fa是采样定理的基本要求；M*2*fa中，M就是过采样率，过采样率是对‘采样定理的最低采样频率’而言的。

过采样率M每提高4倍，可以让ADC分辨率B提高1bit。举例如下：

过采样率分别为4、16、64，ADC分辨率B分别会提高1、2、3bit。这个后面会继续深入介绍。

具体原理与实现，公众号会继续更新。

然而过采样并不是一直都有效的，它也会有限制因素，这个也是后话，咱们后面一一说明。

傅里叶变换的提出让人们看问题的角度从时域变成了频域，多了一个维度。快速傅里叶变换算法的提出普及了傅里叶变换在工程领域的应用，在科学计算和数字信号处理等领域，离散傅里叶变换（DFT）至今依然是非常有效的工具之一。

比如下图是一个幅度为1、频率为2Hz的正弦波和它的离散傅里叶变换后的结果。

可以得到原始matlab代码

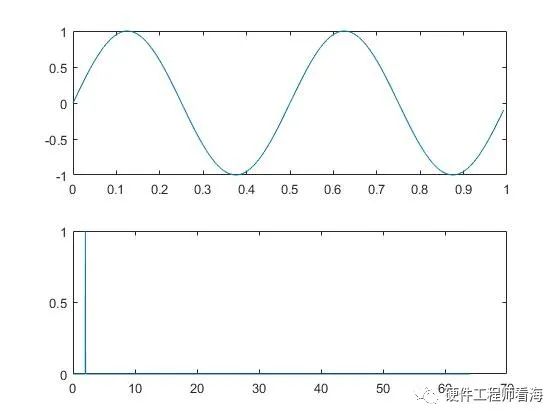
信噪比（SNR）是信号与噪声的比率，它是衡量通信或模拟系统性能的重要指标之一，与傅里叶变换更是有千丝万缕的联系。在很多情况下，我们是通过傅里叶变换来评估信噪比，如果评估方法不对，很难的到我们期望的结果，经常会事与愿违。

求解SNR的过程，我们是用‘评估SNR’来描述，这就是说我们无法精确计算出SNR，只能进行评估，事实也是如此。

评估SNR的方法分为时域和频域两种。我们以一组离散样本点为分析目标，看下如何评估SNR，及其误区。

时域估计SNR

Xs(n)为信号序列，Xn(n)为噪声序列，则信号X(n)=Xs(n)+Xn(n)，是一组带噪离散序列，在时域上评估X(n)的信噪比公式如下：

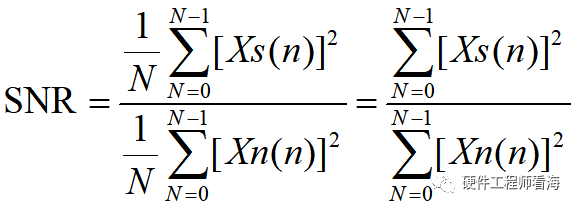
其意义为分别求取离散信号、噪声功率和，计算二者之比。这里有个前提是，我们需要分离出信号与噪声，然后才能求解，

然而问题也在于此，对于一段给定的离散时间序列，我们很难完全分离出信号和噪声，所以时域评估SNR是有局限性的，而且不够直观，所以通常我们在频域下求解。

频域估计SNR

在频域上的SNR计算原理和时域很接近，还是求信号功率与噪声功率只比。最简单的方法是在频谱X(m)上设置阈值，阈值之上为信号，阈值之下为噪声。这样就会有阈值设置带来的估计准确性问题，同时信号频带范围内或多或少也会有噪声叠加进来，在频域计算SNR也是一个近似。

SNR以dB作为单位，SNR(dB)=10*log10(SNR)。

我们往往使用Matlab评估SNR，Matlab是非常强大的数学工具，其集成了SNR计算函数，如果应用不正确，误差会非常大，无法得到预期结果，举例如下。

下图是一个幅度为1、频率为2Hz的正弦波和它的离散傅里叶变换后的结果。

用Matlab SNR函数计算计算信噪比的结果如下，蓝色为感兴趣的信号成分，橙色为噪声。这个频域图就可以表征SNR，橙色的噪声数值越小、越低，说明信噪比越高、越好。即使红色圆圈部分有一点噪声，在评估单频率成分信号的SNR时，这依然是一个非常有效的手段。

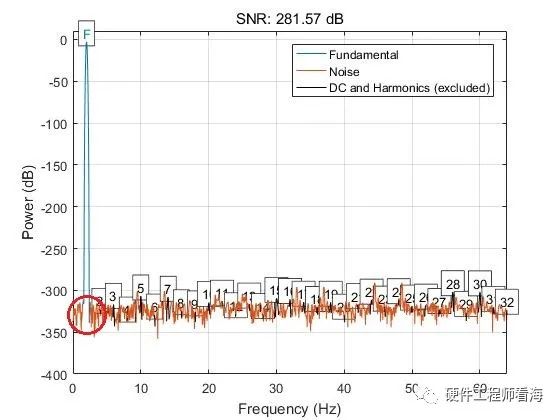
假如一信号x(n)=sin(4pi*t)+0.5*sin(18pi*t),如下图是一个幅度为1、频率为2Hz的正弦波叠加幅度为0.5、频率为9Hz的正弦波的结果。

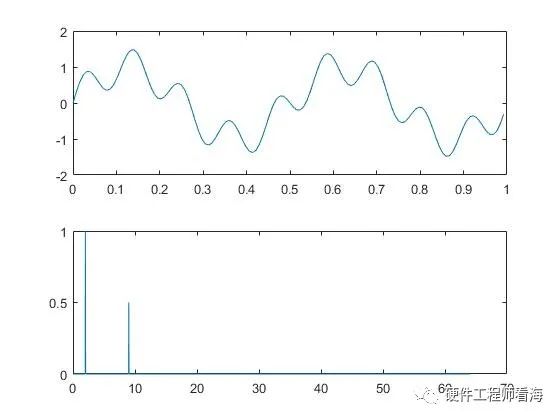
用Matlab SNR函数计算计算信噪比的结果如下，蓝色为感兴趣的信号成分，橙色为噪声，matlab舍弃了频率为9Hz、能量少的成分，只计算了2Hz信号的信噪比。

所以倘若我们的感兴趣信号比较复杂，就不能直接用SNR函数直接计算。

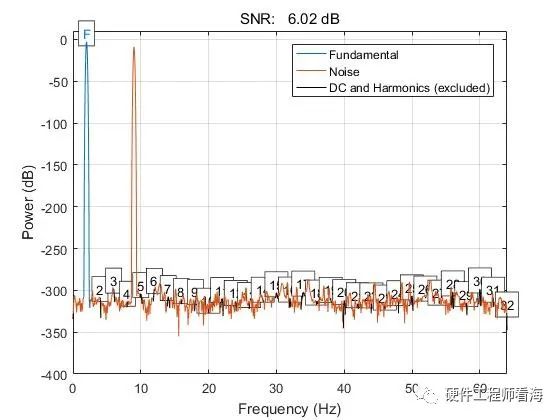
所以我们一定要在理解DFT与SNR关系的基础上，正确使用matlab才能得到期望的SNR结果。

在过采样中，信噪比、ADC有效位数、过采样率是有千丝万缕的联系，了解了基本的概念后，我们一步一步理解过采样的原理。

数字世界是模拟世界的镜像，而ADC就是连接两个世界的大门。一切模拟信号一旦经过ADC离散化后，其幅值必然会失真，其重要原因是ADC分辨率有限，只能逼近真实幅值。

我们不可能抵达真理，只能无限的接近真理。

分辨率是ADC的重要参数之一，它和精度是两个不同的量，精度描述的是离散结果的准确性，而分辨率描述的是ADC能够分辨的最小信号，为1LSB。

换言之，分辨率高的ADC能区分出更小的信号，但其转化的结果准确性受精度限制。

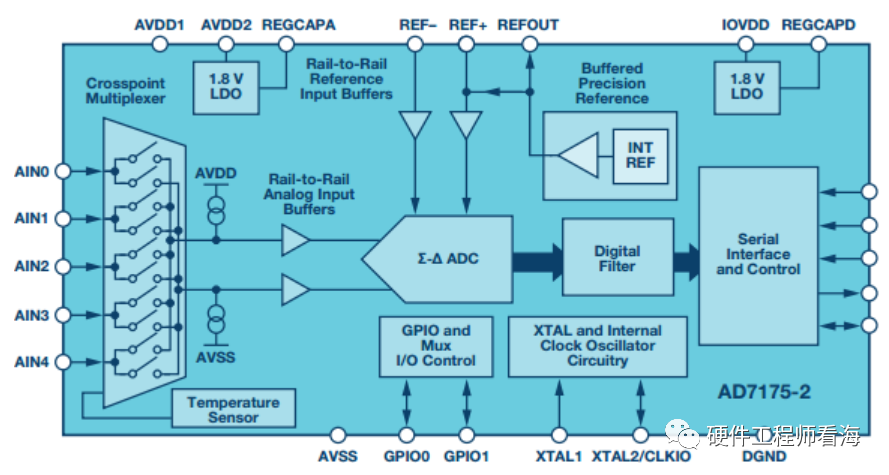
一个8bit ADC，可分辨出256种电平，当输入范围是2.56V时，1LSB即为10mV。受分辨率限制，ADC输出值和实际值之间存在误差。

下图是量化误差的示意图，对于变化小于1LSB的信号，ADC是无法区分出来的，输入和输出此时的误差即为量化误差。

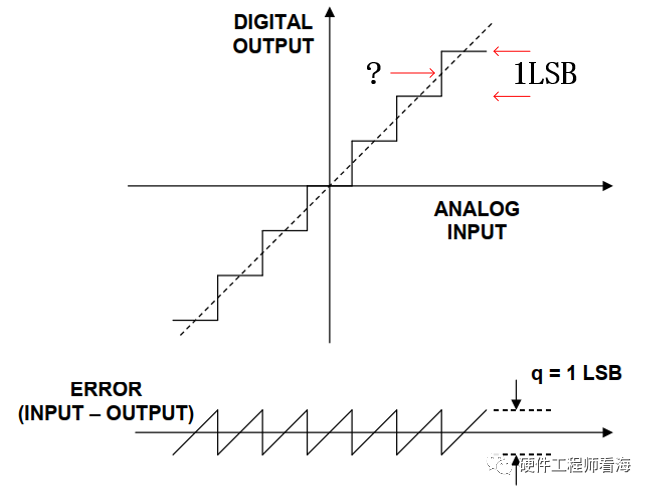
量化噪声的简化数学模型如下，

e(t)=st, -q/2s < t < +q/2s

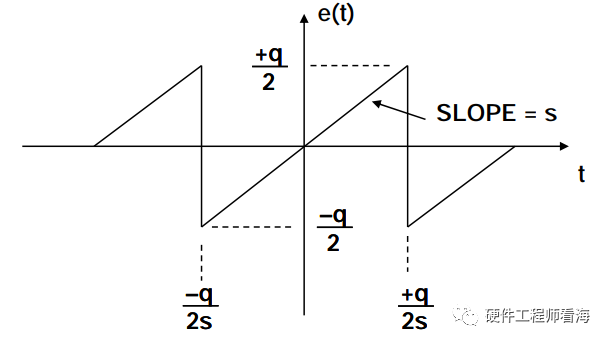
根据输入信号、ADC分辨率和量化误差的关系，我们可以推导出一条重要的SNR计算公式。详细推导过程在公众号后台回复：过采样

下面就是经典的ADC SNR计算公式。

SNR = 6.02N + 1.76dB

 DC至fs/2带宽范围

如果使用数字滤波来滤除带宽BW以外的噪声成分，则等式中还要包括一个校正系数

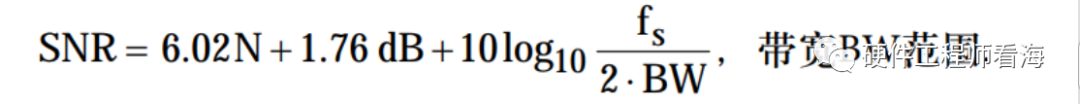
或者写作

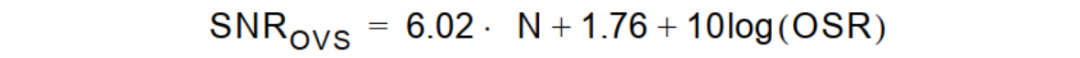
BW是信号带宽，FS是采样率，OSR=Fs/(2*BW)就是过采样率。

我们所说的过采样率每提高4倍，可以提高ADC 1bit的有效分辨率就是根据上面的公式来的，过采样率可以参考以前文章：

过采样系列一：采样定理与过采样率

为什么“过采样率每提高4倍，可以提高ADC 1bit的有效分辨率”？

举个栗子：

当过采样率OSR为1时，

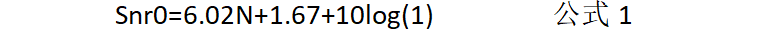
当过采样率OSR为4时，

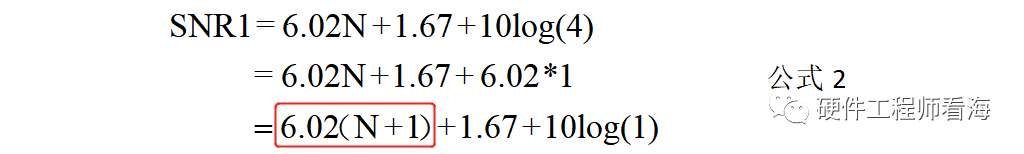
对比公式1和公式2，只有红色框部分不同，即过采样带来的SNR收益和增加分辨率N是可以转化等效的。

额外增加的位数N+：

N+=10log(OSR)/6.02，

当OSR=1,4,16，，，，时，N+=1,2,3，，，，，

这就是通常所说的，过采样率每增加4倍，可以提高1bit分辨率的原因。

那么是不是只要提高采样速率就可以提高分辨率了呢？

其实不对，从公式2可以看出，10log(4)变为10log(1)了，这个过程还需要降低采样，或者下抽，这么做除了降低数据量外，就是可以提高分辨率。

如何下抽，是一个学问，如果简单的求平均，往往只提高信噪比，达不到提高有效位数的目的，好多人在这里会采坑。

如何正确使用下抽来增加有效位数？量化误差与过采样率最经典的解释是频谱密度解释，篇幅有限，后面文章都会持续更新。

这应该是过采样系列的最后一篇文章，经常有同学在使用FPGA、单片机或者DSP进行过采样时没有正确设计代码，导致结果异常，有些结果看似正常，而实际却没有意义。

这篇文章涉及到简单的整型数据和算术运算，希望能有所帮助，仅供参考。

举栗子，理想的8 bit ADC，编码范围是0-255，在参考电压是255mV的情况下，分辨率是1mV。

对一个理想的9.6mV直流电压进行采样，ADC无法分辨小数点后的0.6mV，采样结果会被编码为10，即10mV。

过采样有效是有前提条件的，在这里是对9.6V的直流电压加随机噪声。

过采样

对叠加噪声后的信号进行4次采样，理论上应该得到[9.8, 9.6, 10.4, 9.6]4个离散的样本点，而受到ADC分辨率的限制，实际只能得到[10, 10, 10, 10]4个编码样本，所有样本点都只能分布在。。。8、9、10。。。整数上。

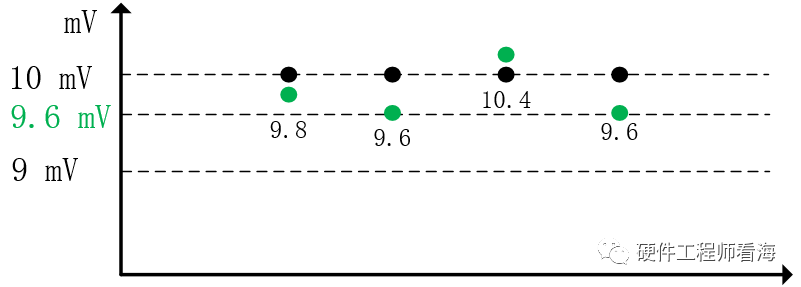
接下来就对这4个样本点详细介绍，直观的感受过采样的原理。

假设信号带宽为B，我们分别分析采样频率F为2B sps/S和8B sps/S两种情况。

当采样频率为2B时，过采样率OSR1=F/(2B)=1;

当采样频率为8B时，过采样率OSR4=F/(2B)=4;

OSR4/OSR1=4，即过采样率提高了4倍（注意：是提高了4倍），其分辨率应该会增加1bit。

过采样系列一：采样定理与过采样率

继续以上面采样9.6mV信号举栗子。

当以采样频率F=1采样时，采集的结果是[10, 10,10, 10]中的任意一个，对应二进制(0000 1010)。

当以采样频率F=4采样时，采集的结果是[10, 10,10, 10]4个序列。

下面对F=4的4个数据进行下抽处理（降采样），可以减少计算量增加分辨率。

抽取

ADC是8bit的分辨率，但是在过采样计算时，不能定义并初始化一个8bit的整形数据，如果初始化8bit的数据，计算过程会溢出，最终结果的位宽还是8bit，并没有增加分辨率，在这里我们定义一个16bit的数据，预留了足够的buffer。

对采样得到的4个8bit数据求和运算，需要计算最大位宽，求和后的最大位宽为8+2=10bit，相当于左移了2bit，变为10bit。

如果只是简单的求平均，求和后的结果再除以采样个数4的话，则数据其实是右移2bit，又变回原来的8bit位宽，并没有增加分辨率。

在这里我们选择下抽方法是求和后除以2，即右移1bit，则数据从10bit变为9bit，相比于原始的8bit，增加了1bit分辨率（过采样容易理解，更重要的是下抽）。

过采样系列三：量化误差与过采样率

过采样率为4时，采样的4个数据序列[10, 10,10, 10]求和后是40，对应二进制(00 0010 1000)，右移1bit后变为20，对应二进制(0 0001 0100)

255mV参考电压下，原始的8bit ADC，分辨率为1mV，采集的数据是9(0000 1001)，即9mV；

过采样率增加4倍后：

255mV参考电压下，9bit ADC，分辨率为0.5mV，采集的数据是20(0 0001 0100)，即10.0(9.98)mV；

过采样率增加4倍的前提下，只提高了1bit分辨率，效果不是很明显，继续在9.6mV基础上添加随机噪声，这次过采样率再增加4倍，达到16倍，即采样速率F=16，对16个采样序列进行计算举例。

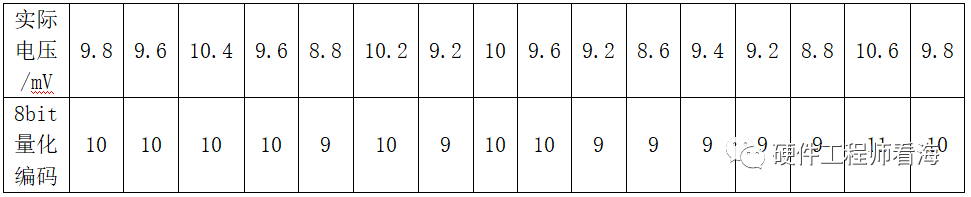
对采样得到的16个8bit数据求和运算，最大位宽是8+4=12bit。

求和：10*8+9*7+11=154，对应二进制是(0000 1001 1010)，再右移2bit，则变为10bit的38(00 0010 0110)，（再次强调，不能简单的求和然后求平均）。

9.6mV加噪信号：

1、255mV参考电压下，原始的8bit ADC，分辨率为1mV，采集的数据是10(0000 1001)，即10mV

2、过采率为4后：

255mV参考电压下，9bit ADC，分辨率为0.5mV，采集的数据是20(0 0001 0100)，即10.0(9.98)mV；

3、过采率为16后：

255mV参考电压下，10bit ADC，分辨率为0.25mV，采集的数据是38(00 0010 0110)，即9.47mV；

从列举的例子可以看出，过采样率是可以提高分辨率的，但是提高采样速率来提高分辨率的代价是巨大的（牛顿第三定律：得到点东西时总要舍弃点什么^_^）。

－ The End －

声明：欢迎转发本号原创内容，转载和摘编需经本号授权并标注原作者和信息来源为云脑智库。本公众号目前所载内容为本公众号原创、网络转载或根据非密公开性信息资料编辑整理，相关内容仅供参考及学习交流使用。由于部分文字、图片等来源于互联网，无法核实真实出处，如涉及相关争议，请跟我们联系。我们致力于保护作者知识产权或作品版权，本公众号所载内容的知识产权或作品版权归原作者所有。本公众号拥有对此声明的最终解释权。

投稿/招聘/推广/合作/入群/赞助 请加微信：15881101905，备注关键词

“阅读是一种习惯，分享是一种美德，我们是一群专业、有态度的知识传播者.”