激光雷达发射与回波信号处理

1 雷达信号的表示方法

雷达信号波形、调制载频、调制相位均是已知的。雷达信号所占有的频率宽度通常远远小于调制载频。因此雷达信号是一种窄带高频信号。

1.1  实信号表示法

雷达信号可以表示为时间的函数：

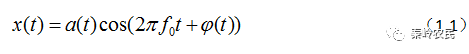
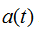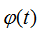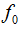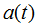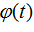式中为雷达信号的调幅包络，为雷达信号的调制相位，为雷达信号的调制载频。由于常用的雷达信号是窄带信号；亦即和与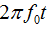相比是时间的慢变化函数。在这样的情况下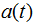，称为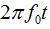载波的包络。

1.2  复信号表示法

实信号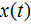上添加适当的虚数项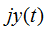，便构成复信号

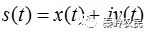
，这样尝尝可以简化雷达信号和滤波器的分析。用复信号作分析之后用取复信号的实部的方法就可以得到实信号。实信号由（1.1）式给定。将余弦变成正弦便可得到虚数项：

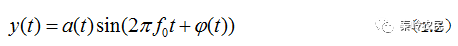
复信号表示式为：

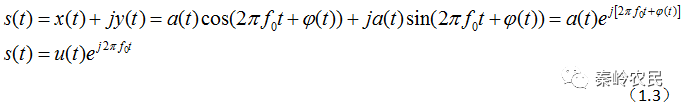
式中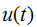是复载波的复调制函数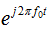，并由下式给定：

1、3 雷达信号的能量和特点

如果把实信号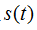看做单位电阻上的电压或者通过的电流，则实信号的能量为

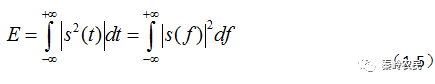
而复信号的能量为

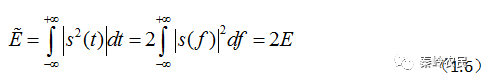
显然，当雷达信号设计确定，则雷达信号能量就是一个定值，它是一个常数。总之雷达信号即可用实信号表示，也可以用复数表示，只不过复数表示更为方便。因为只要确知雷达信号复包络以及其频谱，就可以对雷达系统进行最佳设计了。

2        雷达信号接收

雷达信号回波信号和发射信号的区别仅限于以及多普勒频移。如果略去了鉴别目标的其他参数，同时一些与发射波形无关的因素，如距离衰减，天线方向特性等也不考虑进去，并不考虑目标运动加速度在信号持续期内可以忽略的场合。

2.1  回波数学模型

设“点目标”以恒定的径向速度v接近雷达，则目标距离可用下列方程表示

如果发射信号为：

回波信号的数学表达式可以写成

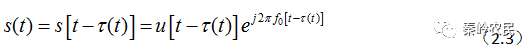
其中时延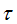为时间的函数，即

将（2.1）带入上式

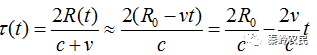
再带入到（2.3）式可以得到

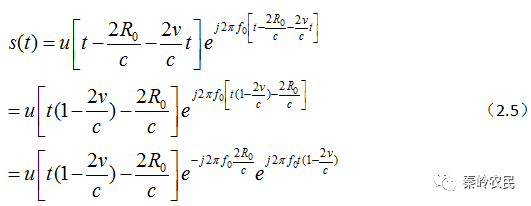
令

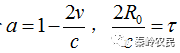
，为目标回波的延时，

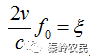
为目标回波的多普勒频移。上式可以写为

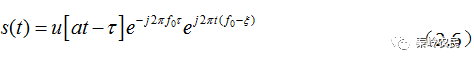
上式表明，

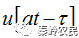
为振幅，表现为回波信号的复包络。目标运动速度对目标回波信号有两个方面的影响：1）信号复包络的时间比例发生变化；2）载频移动。

在实际应用中，第一项影响常可以忽略不计。因为多普勒效应引起的复包络最大失真将出现在脉冲后沿，如果T为脉冲宽度，则脉冲后沿处信号复包络的时间差为

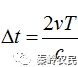
。如果信号的带宽为B，只要在1/B 秒内信号复包络没有显著变化，即当

或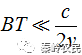时，第一项影响就可以忽略不计，于是，多普勒效应可以简单视为载频偏移。通常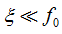，回波信号的表达式就可简化为

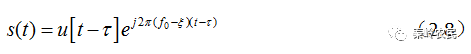
3      模糊函数

模糊函数最初是在研究雷达分辨率问题中提出的一个概念，从衡量两个不同距离，不同速度的目标的分辨度提出的模糊函数的定义式，采用均方差准则作为最佳分辨准则。通过这一个函数定量描述当系统工作多目标下，发射一种波形并采用响应的滤波处理，系统对不同距离，不同速度目标的分辨能力。模糊函数回答了发射什么样的波形，在采用最优信号处理的条件下系统具有什么样的分辨率，模糊度，测量精度和杂波拟制能力。也就是说，当干扰目标与观测目标之间存在着距离和速度差别时，模糊函数定量地表示了干扰目标对观测目标的干扰作用。

如以观测目标1为基准，并设基准目标1为临近目标，具有时延x和多普勒频移y，则由（2.8）式子可得到目标1的回波信号表达式为

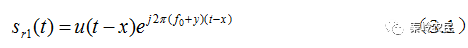
如果目标2为干扰目标距离雷达比1目标远，也是临近目标，而且径向速度更大。即目标2相对于基准目标1具有时延和多普勒频移，那么目标2回波信号的表达式将是

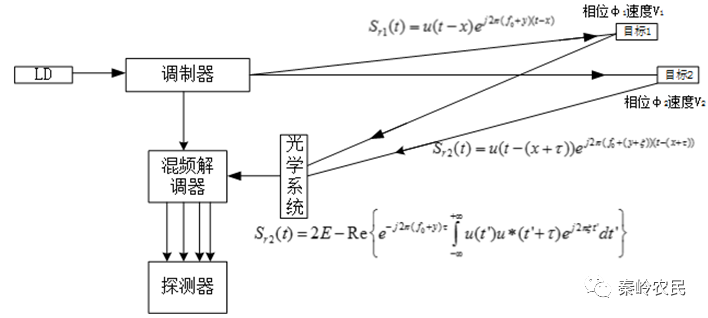
图1 模糊函数反射信号图

于是两个目标回波信号的均方差可以写成

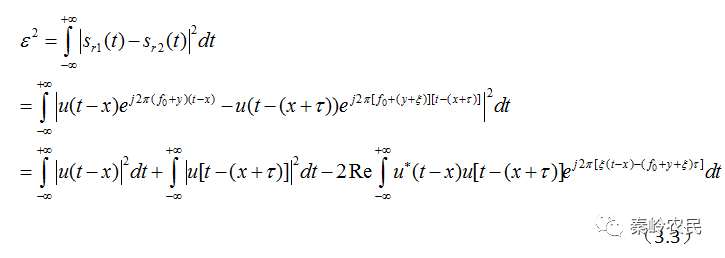
其中

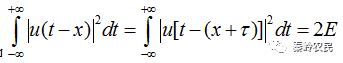
令

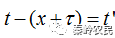
，则上式可简化为：

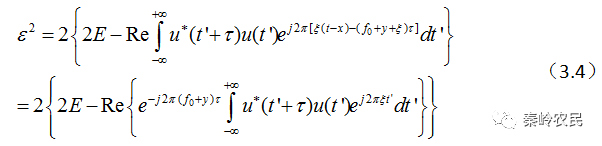
令：

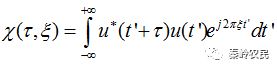
。为信号的复包络的时间-频率自相关函数。则上式可以改写为

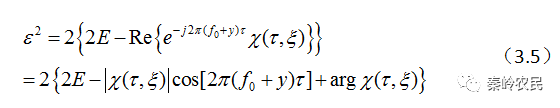
又因为

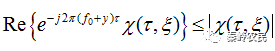
，所以，

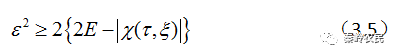
式（2.14）就表明

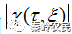
是决定相邻目标分辨率的唯一因素，它越大，

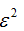
越小两个目标就越难以分辨，也就是模糊度越大。而

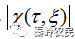
是随着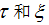的增大而下降，同时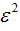就会增大。

由模糊函数的定义很容易得到距离模糊函数和速度模糊函数。

距离模糊函数：

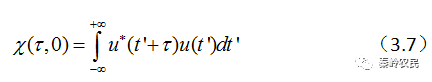
速度模糊函数

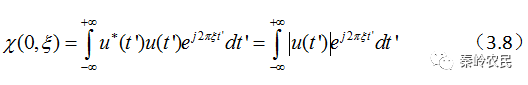
以上是在分辨的角度推导模糊函数，模糊函数也可以由匹配滤波器的响应导出，设信号复包络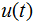的频谱为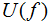，根据匹配滤波器理论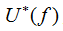，为此信号匹配滤波器的频响。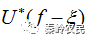表示匹配滤波器所匹配的频率与信号频率相差一个值。信号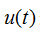通过此频率偏移的匹配滤波器后，输出信号的频谱为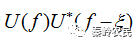，对应输出波形为输出频谱的傅里叶反变化：

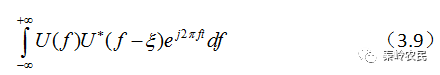
将式中的改写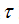成就得到

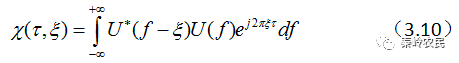
模糊函数的应用很广，除了能确定信号的分辨率外，还可以用来分析信号本身所具有的测量精度、杂波拟制性能和模糊情况等。

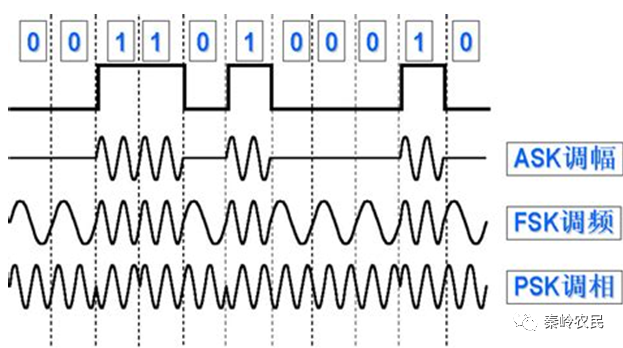
图2 信号调制图

4         二项编码

二项码由于实现简单更具有实际应用意义，它将脉冲宽度分为许多等宽的子脉冲，每个子脉冲以0，π，进行相位调制。其调制的顺序由制定的编码序列决定。常见的二项码序列包括巴克码，m序列，L序列等，相关的理论也较为成熟，已经能够在实际中应用。

4.1  相位编码信号

一般的相位编码信号的表达式

信号的复包络函数为

对于二项编码来说的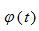取值为0或者π，对应于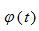可以用二进制相位序列

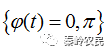
表示，也可以用二进制序列

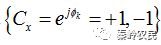
表示，有时也可用序列

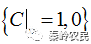
表示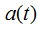，在无线电波领域雷达发射不同无线电波波形的窗函数。对于脉冲二相编码信号，该窗函数是一个矩形窗，窗宽为脉冲宽度。对于连续波二相编码信号而言，则恒为1。为了统一两者形式，都做矩形窗处理。

其中N为码长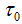，为子脉冲时宽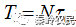，为信号持续时间，则二相编码的复包络可以写成：

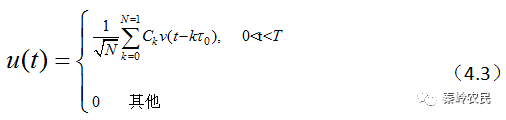
其中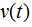为码元波形，利用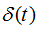函数性质，上4.3可以写成：

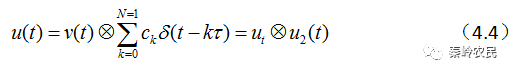
其中

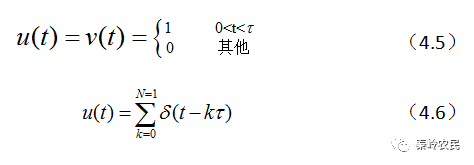
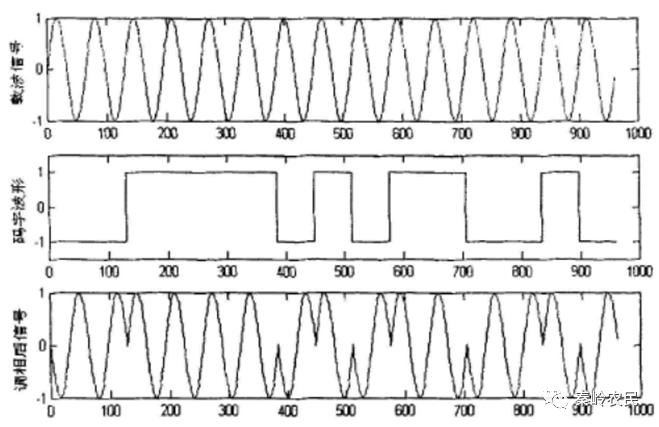
图3 二相编码时域调制图

4.2  相位编码回波

首先由二相码产生器产生码字，主要产生伪随机码或者随机码。码字一路输入调相器，对本振光信号进行调相，经过功率放大后发射出去，另一路把码字存储起来形成参考码，以便与混频后的视频信号进行相关处理。回波信号经过与本振光信号混频，得到视频信号；再经过视频放大和A/D转换后，编程离散的数字信号；最后由信号处理机对这些数据进行处理，获得需要的目标信息。

一般相位编码信号的复数表达式可以写成

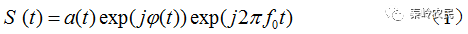
信号的包络函数为

其中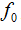为载波信号的频率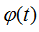，为相位调制函数。对二相编码信号来说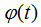，只有0和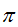两个可能得取值。

信号发射出去后，遇到目标反射回来，而回波信号被天线接收，此时的回波与发射相比，本质上只是多了一个延时信息t_r，即为

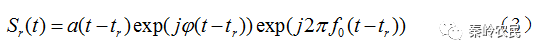
如果是幅值不变，可以将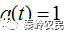。设运动目标相对雷达基站径向匀速运动，目标的速度为V_r，t=0时刻距离雷达为R₀，则在t时刻收到的回波是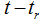在时刻发出的，而照射到目标上的时间是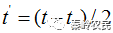，那么照射时目标距离为

往返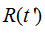的时间为信号延迟时间，即

联立上式得到

将带入上面

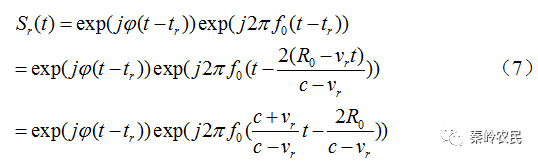
由于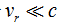

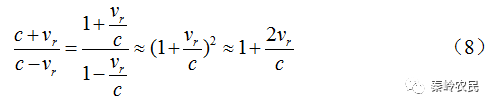
并令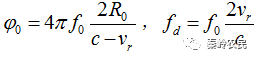。其中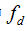为多普勒频率。

于是得到信号光为

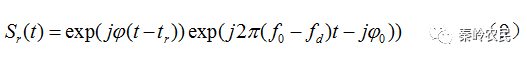
经过混频后去掉得到的差频信号为

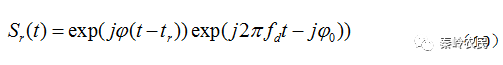
从上式可以看到，回波信号与发射码字相比，多了两个参数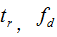，依次反映了目标的距离和速度信息。对回波的信号的检测也主要是对这两个参数的检测。雷达接收机接收的回波信号在经过混频和DDC处理后的基带信号中，既存在码字延时又存在新的包络，延时是对目标距离信息的反映，而包络的频率则是目标速度的体现。在信号处理中，对延时信息和包络频率的提取就完成了目标距离和速度的提取。