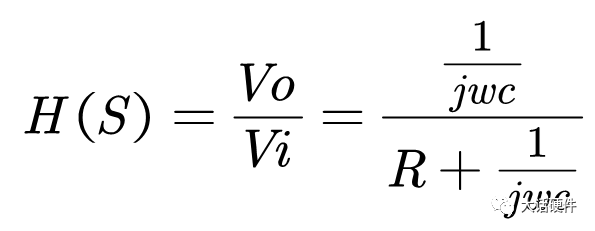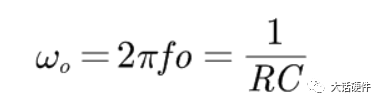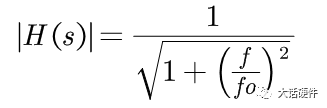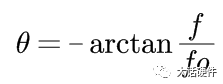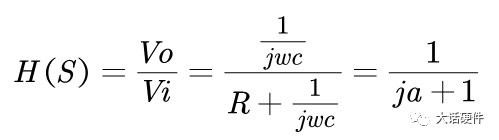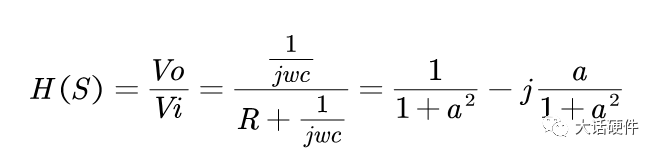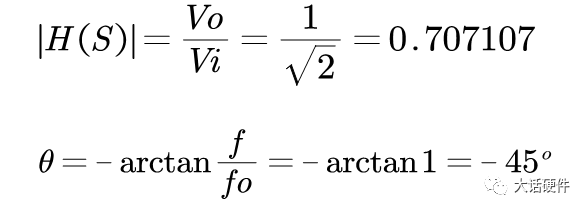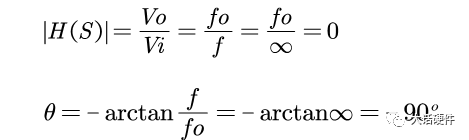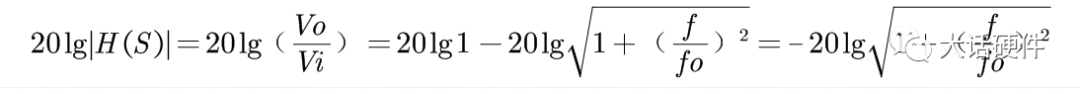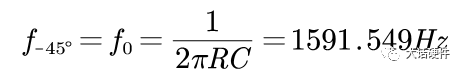来源 | 大话硬件
智库 | 云脑智库(CloudBrain-TT)
云圈 | 进“云脑智库微信群”,请加微信:15881101905,备注您的研究方向
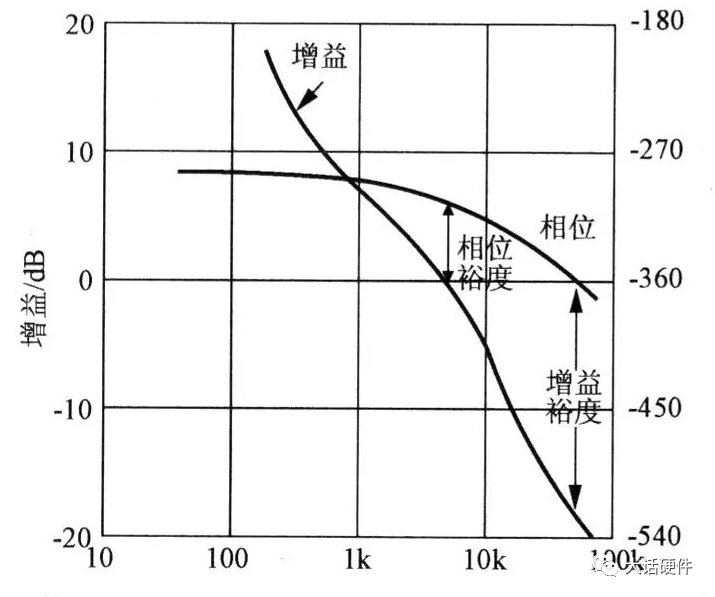
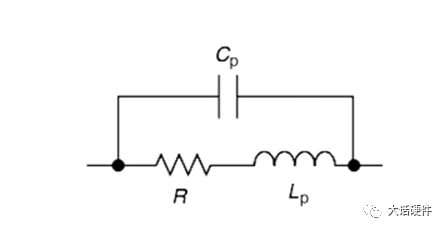
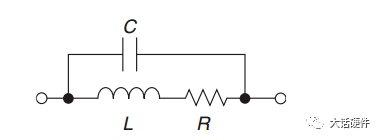
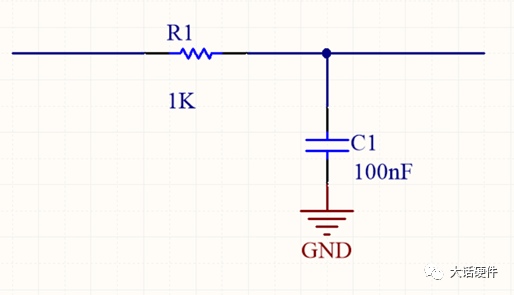
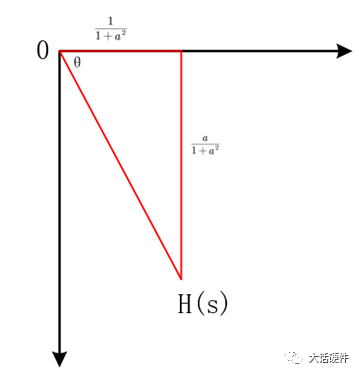
最近因为项目需求,在回看波特图方面的内容。大三那会,《自动控制原理》这本书里面就讲过这些东西,但是那时候总感觉学这些没啥用,反正以后也用不到,对这种课程的重视度不是很高。工作后发现,只要你从事的是和本专业相关的工作,大学学过的很多理论课程在后面大概率都会用到。曾经那些我们在学校以为用不上的东西,熟不知在后面用处还多着呢。所以啊,仅仅只是我们的以为而已!现在还在学校的同学,对待《自动控制理论》、《信号与系统》、《通信原理》这样的核心专业课,建议还是好好学习一下,认真听听课。哪怕是考试完以后就会忘掉,但当我们再次捡起书本时,或多或少还是会些模糊的记忆存在。相比完全没怎么听过课的人来说,学起来也会更快。今天这篇文章想把近段时间关于波特图方面学习的内容整理一下。波特图将会是梳理闭环控制这个系列的开始。目前的计划是,以无源器件为基础,然后结合运放,再过渡到开关电源的环路控制方面。如果对这方面感兴趣的朋友,可以持续一起学习起来,目标就是掌握开关电源的闭环控制。波特图最常见的应用是在线性非时变的系统中,用于对传递函数的增益和相位进行分析,从而判断出系统随频率的响应是否稳定。因此,波特图又称为幅频响应和相频响应曲线图。理想的电阻,无论输入什么样的信号,在增益和相位上,不会有变化(忽略电阻产生的压降)。毕竟只要有电流流过电阻,输出端相比输入端的电压肯定会有略微降低。因此,使用波特图研究理想电阻对输入信号的响应,没什么意义。而在真实的世界中,电阻由于生产工艺制造,PCB板上走线,SMT焊接等一系列的操作,理想的电阻,并不是我们想象中的那样。只要把电阻用在电路中,它就会自带寄生电感和寄生电容,实际的等效模型如下所示:我们知道,电容和电感的阻抗会随着频率的改变而改变。那么实际的电阻也会信号频率的改变产生响应。理想电阻对不同输入信号的频率没有响应,无论在什么条件下,它一直表现出来同样的阻抗,在全频率范围内,阻抗一直会保持同样的阻值。但是结合电容和电感的等效模型可知,实际的电阻并不会一直保持同样的阻抗。综上可知,真实的物理世界中,无论是独立的电阻,独立的电容,独立的电感,都会对输入信号的频率有响应。不同频率的信号通过这三者组成的电路,所得到输出信号幅度和相位会有区别。从上面的分析可以看出,现实世界中的电子元器件,电阻,电容,电感都会对输入信号频率的改变产生响应,而半导体器件由于CMOS工艺的原因,会在半导体管极间产生寄生电容,加工制造的PCB走线,会有寄生电感的存在。所以,加工制造完毕的、实际的PCBA单板,输出信号都是会受到输入信号因频率改变而带来的的影响。既然是这样,那么波特图就能很好的帮助我们分析电路对信号频率改变的响应了。滤波器的作用是对不同频率输入信号,实现不同的增益和相移,以形成输出。对设计滤波器的人来说,比较关注的是在特定的频率内,到底有怎样的增益和相移。根据前面分析的内容,波特图刚好是研究增益和相移。所以要想设计一个满足性能的滤波器,必须要学会波特图。下面以一个低通滤波器为例,讲述如何分析和使用波特图。输入信号为VI,输出信号为Vo,根据电阻分压的原理,可以计算出RC低通滤波的传递函数为:从传递函数可以看出,传递函数受到输入信号频率ω的影响。要知道Vi信号经过RC后的变化,就需要了解H(s)的特性,为了便于分析,令根据复数性质,计算出H(s)的幅值和相位大小分别为:关于传递函数的幅值和相位计算,目前很多书上都是直接给出答案,这里推导一下结论的来源。为了方便计算,可以令传递函数为下面的这样的形式:
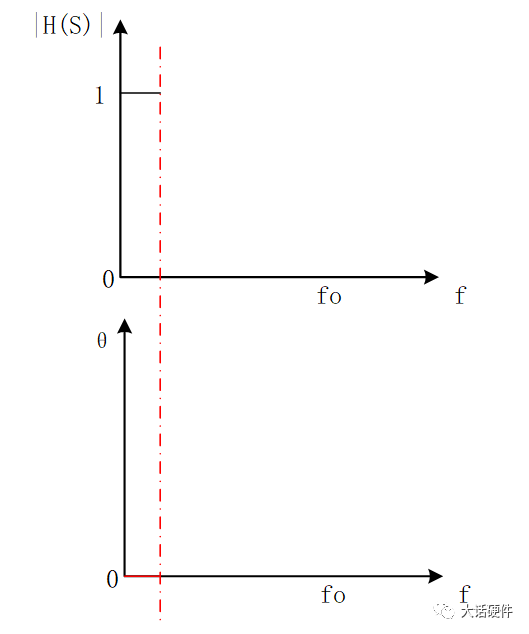
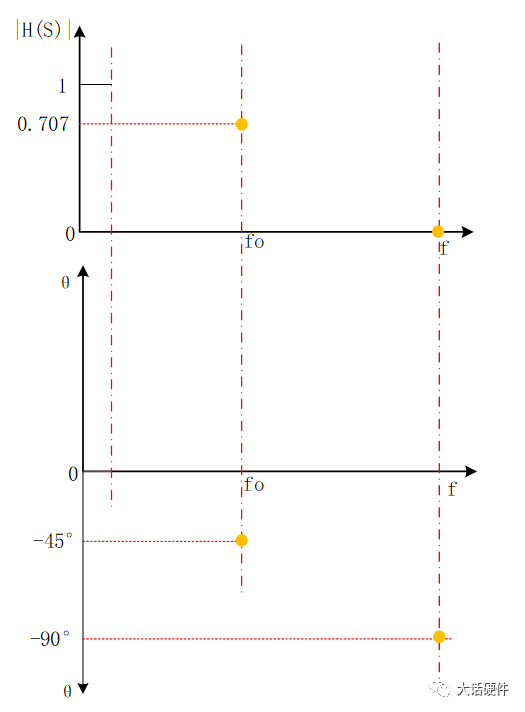
求H(S)的幅值和相位,需要对其分子分母有理化,可以计算得到:幅值和相位根据下面的坐标图,就能计算出上面幅度|H(s)|和相位θ的大小。根据|H(s)|的表达式,1和f/fo之间的关系大小,会使|H(s)|有不一样的结果。因此,1和f/fo之间的关系,将|H(s)|分为三个阶段。f远小于fo,可认为输入信号为直流信号,此时H(S)的增益和相位表达式中将f/fo这一项忽略。则增益为1,输出信号幅值等于输入信号幅值。此时相位θ也非常小,几乎为0。也就是说,在f非常小时,输出跟随输入变化,幅度不变化,相位也不变化。
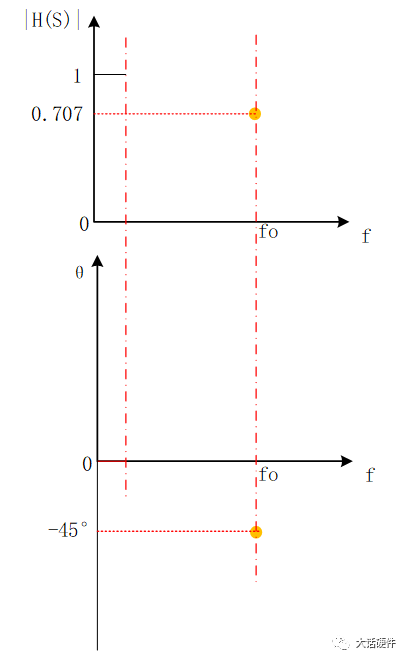
输入信号频率f刚好和RC乘积相等,此幅值和相位的大小为:
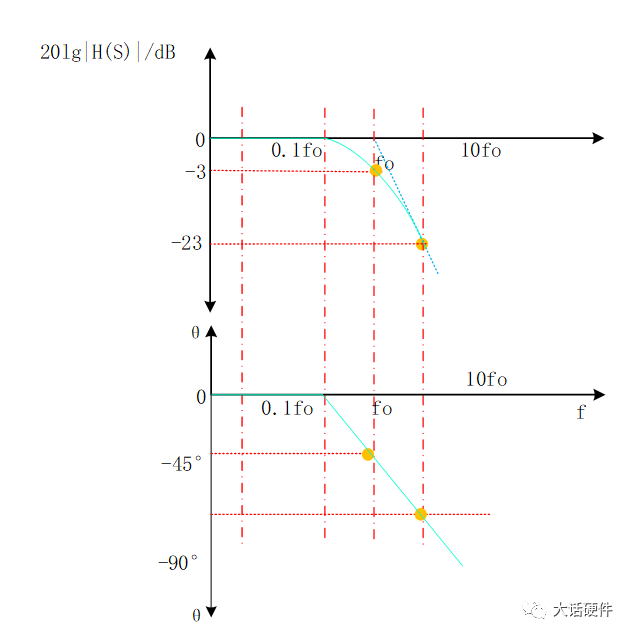
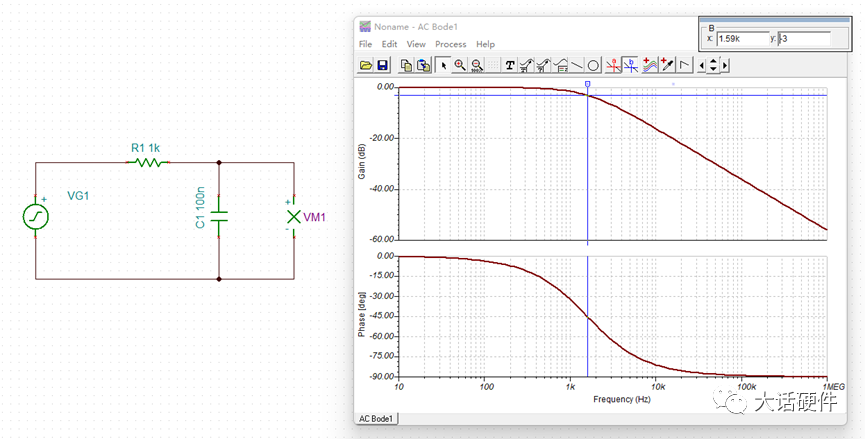
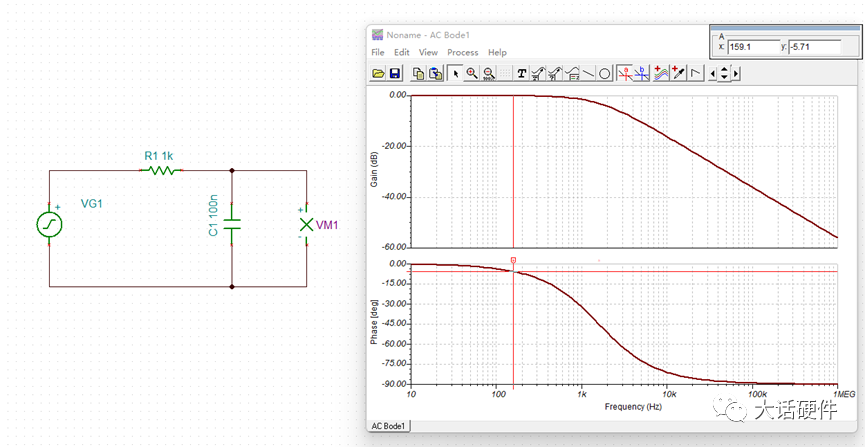
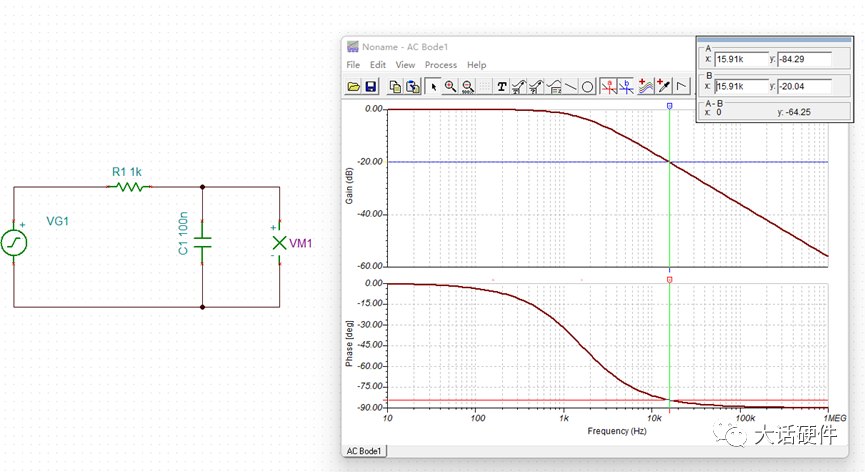
根据上面的内容,我们只能分析出f在很小时和f=fo时的幅值和相位,画出来的增益和相位曲线如图13和图15所示,在f趋近于fo的过程中,幅值和相位是怎么样的变化的还不知道。先不着急得到变化趋势,接着把第三阶段分析完。根据输入信号的变化和传递函数的表达式,我们推出了全频率范围内输出信号的变化。可以得到的结论是:在RC滤波电路中,输入信号的频率越高,输出信号频率越少,而且相位滞后越大。当f非常小时,输出信号在增益和相位和输入信号保持一致。当f非常大时,此时输出端的信号几乎为0,相位滞后90°,且此时研究相位也没有意义。波特图可以研究系统的频率响应,且能描述增益和相位,而增益和电压放大倍数刚好能对应起来,所以RC电路的响应,也可以用波特图进行描述。根据波特图的定义,XY轴坐标需要改为对数坐标,即横轴用lgf来表示,纵轴用20lg(A)来描述。将RC电路输入输出增益和相位响应曲线,幅值和频率换成对数坐标系后:由H(s)的对数公式可知,只有在f>>fo 时,斜率才是-20dB/10倍的频程,在0~-3db之间,这个关系式并不成立。在波特上,按照0.1fo的频率作为增益和相位更改的起点,代入关系式中,可以计算出增益误差为-0.04dB,相位误差为-5.71°。可能有人会有疑问,为什增益和相位的变化要从0.1fo开始,是0.01fo不行吗?结论是,研究0.01fo没什么意义,代入到公式可以计算出,此时增益基本为0dB,相移基本为0°,所以在低频阶段,曲线一直和坐标轴保持一致。使用TI的TINA软件对RC电路进行仿真,看输出信号随着输入信号变化趋势。其中比较特殊的点为产生-45°相移频率,即输入信号频率和fo的频率相等,可以计算出分析波特图,输入信号频率为1.59KHz时,输出信号相比输入信号产生了-45°的相移,此时的增益为-3dB。也就是输出信号是输入信号的0.707倍,信号被衰减了。分析波特图,输入信号频率为159.1Hz时,增益基本为-0.04dB,相移为-5.71°。此时输出信号和输入信号基本可认为是一样的,误差比较小。分析波特图,输入信号频率为15.91KHz时,增益基本为-20.04dB,相移为-84.29°。此时输出信号为输入信号的0.0995倍,衰减的非常厉害。研究波特图增益和相位曲线并不是最终目的,它仅仅是我们分析一个电路对输入信号频率响应的手段。通过观察波特图的增益和相位曲线,可以很好的分析出输出信号在不同频率点上增益是多大,那么就知道到底能提取出来多大的输入信号。分析出输出信号在不同频率点的相移,可以知道系统是否有产生自激振荡的风险。
对于滤波器来说,如果知道该滤波器的波特图,那么无论输入多大频率的信号,都可以计算出输出信号有多大,相位是怎样变化,从而很轻松的达到了我们想要的结果。- The End -
声明:欢迎转发本号原创内容,转载和摘编需经本号授权并标注原作者和信息来源为云脑智库。本公众号目前所载内容为本公众号原创、网络转载或根据非密公开性信息资料编辑整理,相关内容仅供参考及学习交流使用。由于部分文字、图片等来源于互联网,无法核实真实出处,如涉及相关争议,请跟我们联系。我们致力于保护作者知识产权或作品版权,本公众号所载内容的知识产权或作品版权归原作者所有。本公众号拥有对此声明的最终解释权。
投稿/招聘/推广/合作/入群/赞助 请加微信:15881101905,备注关键词

微群关键词:天线、射频微波、雷达通信电子战、芯片半导体、信号处理、软件无线电、测试制造、相控阵、EDA仿真、通导遥、学术前沿、知识服务、合作投资.
“阅读是一种习惯,分享是一种美德,我们是一群专业、有态度的知识传播者.”
↓↓↓ 戳“阅读原文”,加入“知识星球”,发现更多精彩内容.
分享💬 点赞👍 在看❤️@以“三连”行动支持优质内容!