ADC广泛用于各种应用中,尤其是需要处理模拟传感器信号的测量系统,比如测量压力、流量、速度和温度的数据采集系统……任何设计中,理解这些类型应用的总系统精度始终都是非常重要的,尤其是那些需要对波形中极小的灵敏度和变化进行量化的系统。
理想情况下,施加于信号链输入端的每一个伏特都由ADC以数字表示一个伏特的输出。但是,事实并非如此。所有转换器和信号链都存在与此相关的有限数量误差。本文揭示了转换器内部的不精确性累积到何种程度即会导致这些误差。定义新设计的系统参数时,若测量精度极为重要,那么这些内容对于理解如何正确指定一个ADC有着重要作用。
首先,注意到由于ADC不是理想的,并且分辨率有限,因此它们在输出端只能显示有限数量的信息表示。表示的信息数量由转换器满量程输入除以2N表示,N为转换器的理想位数。
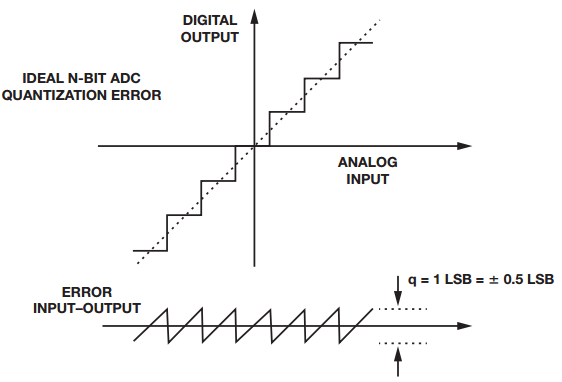
图1. ADC量化误差
例如,假设选择一个12位ADC,则它可在输出端以4096个数字表示施加于转换器输入端的任何信号。这些表示信息确实存在有限量的误差。因此,如果12位ADC的输入满量程(VFS)为10 V p-p,那么其理想情况下的LSB大小为2.44 mV p-p,精度为±1.22 mV。
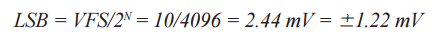 (公式一)
(公式一)
而实际上,ADC是非理想的。在转换器内部存在一定噪声, KT/C甚至直流中也有噪声。记住,1 kΩ电阻等效于4 nV∙Hz (1 Hz带宽,25°C)。注意,查看12位ADC数据手册时,SNR通常为大约70 dB到72 dB。但是,根据下列公式,一个12位ADC理想情况下应当具有74 dB:
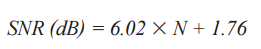 (公式二)
(公式二)
因此,实际上12位分辨率是无法达到的,因为转换器本身存在一定的不精确性,如图2所示。
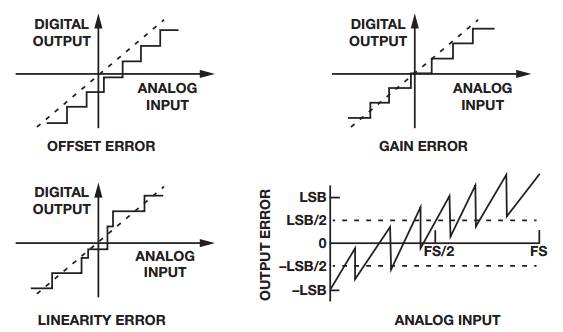
图2. ADC的不精确性
这些不精确性或误差决定了转换器表示信号的效率,并最终为信号链所接收。失调误差定义为传递函数无法通过零点的模拟值。增益误差是失调误差为零时理想与实际传递函数之间的满量程数值之差。通常意义上的线性度误差或非线性度是指零电平与满量程之间的直线偏差,如图1所示。
模数转换器线性度只与转换器自身有关,即取决于架构和工艺变化。有很多方法可以校正,但都很昂贵。设计人员有两种选择:
购买更好、成本更高的转换器,或采用数字手段校正线性度,数字校正的成本也十分高昂,这意味着可能需要更多资源来指定DSP或FPGA,因为线性度会随温度和工艺的变化而改变;
根据采样速率、IF和分辨率,数字校正可能需要广泛的特性表述和查找表,以便即时校正或调节ADC的性能。
线性度有两种类型的误差:它们是差分非线性和积分非线性, 通常分别称为DNL和INL。
DNL定义为偏离理想值的一切误差或偏差。换言之,它表示两个相邻代码的模拟差与理想代码值VFS/2N之间的偏差。可将其看作与ADC的SNR性能相关的因素。随着代码的偏差越来越大,转换数也随之下降。该误差在温度范围内的界限为±0.5 LSB,可保证无失码。
INL定义为零电平和满量程之间的理想直线近似曲率偏差。多数情况下,INL决定了ADC的SFDR性能。INL总偏差形状可以决定最主要的谐波性能。比如,INL曲线呈弓形会相应产生更差的偶次谐波,而INL曲线呈S弓形则通常产生奇次谐波。该误差本质上与频率有关,并与这类误差分析无关。
哪怕可以消除静态失调和增益误差,与失调和增益误差有关的温度系数将会依然存在。
例如,一个12位ADC具有10 ppm增益误差,或FSR/°C = 0.001%/°C。12位系统中的1 LSB为¼096,或者近似等于0.024%。
因此,若125°C ∆ (–40°C至+85°C),则产生±2.5 LSB增益温度系数 误差,或0.001% × 125 = 0.125%,其中,0.125/0.024 = 5.1或±2.55 LSB。
对于失调温度系数,5 ppm失调误差或FSR/°C = 0.0005%/°C。
这将产生±1.3 LSB失调温度系数误差,或 0.0005% × 125 = 0.0625。其中,0.0625/0.024 = 2.6或±1.3 LSB。



