matlab频谱分析时的若干问题解释及几种频谱的理解

一、信号采样问题

在matlab中对以下信号进行采样：

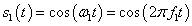
其中f1 = 1000Hz，根据奈奎斯特采样定理，采样频率f ≥ 2f1，在此我们取f = 3000Hz。

在matlab中仿真也好，实际中处理的信号也罢，一般都是数字信号。而采样就是将信号数字化的一个过程，设将信号s1(t)数字化得到信号：

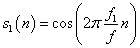
其中n=[0…N-1]，N为采样点数。

我们来解释一下s1(n)，为什么说上式表示以采样率f对频率为f1的信号进行采样的结果呢？采样，顾名思义，就是对信号隔一段时间取一个值，而隔的这段时间就是采样间隔，取其倒数就是采样率了。

那们我们看上式，将前面的参数代入：

当n=0时：

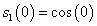
当n=1时：

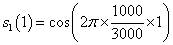
当n=2时：

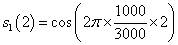
当n=3时：

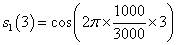
这是不是相当于对信号s1(t)的一个周期内采了三个样点呢？对一个频率为1000Hz的信号每周期采三个样点不就是相当于以3倍于频率的采样率进行采样呢？注意，当n=3时相当于下一个周期的起始了。

我们取采样点数N=64，即对64/3=21.3个周期，共计64/3/f1=21.3ms时长。

我们在matlab中输入以下命令：

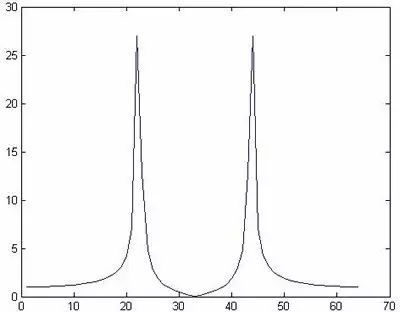
图1

下面我们对图1进行一下解释，以说明图中的横坐标轴的所代表的意义。

对于信号：

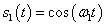
我们知道它的傅里叶变换是：

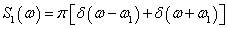
如果在-2π×3000/2 ~ 2π×3000/2范围内观察信号s1(t)的频谱，则应该在2π×1000和-2π×1000两个频点上有两根谱线，而对采样后的数字信号，频率坐标轴范围-2π×3000/2 ~ 2π×3000/2将被归一化到-2π×(3000/2)/3000 ~ 2π×(3000/2)/3000即-π ~ π范围内，因此将在2π×1000/3000和-2π×1000 /3000即2π/3和-2π/3的两个频点上有两根谱线。注意，此时坐标轴上的2π代表着3000Hz的频率范围。

另外还有一点应该明白的是，时域采样意味着频域的周期延拓，即-π ~ π上的谱线与-π+M×2π ~ π+M×2π范围内的谱线是一模一样的，其中M为任意的整数。更通俗的说，a ~ b之间的频谱与a+M×2π ~ b+M×2π之间的频谱是一模一样的。因此-π ~ 0之间的频谱与π ~ 2π之间的频谱是一样的。

在matlab中，如果仅简单的执行plot绘图命令，坐标横轴将是1 ~ N，那么这1 ~ N代表着什么呢？是的，应该代表0×2π，应用到上面的例子即是0~3000Hz的频率范围。

其中1 ~ N/2代表0 ~ π，而N/2 ~ N代表-π ~ 0。

从理论上讲，对于

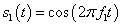
应该在1000Hz和-1000Hz两个频点上有两根线，即应该在x1（其中x1×(3000/2) /(64/2)=1000，解得x1=21.3）上和64-x1上有两根谱线。观察图1可知，两个峰值大约对应横轴坐标为21和43=64-21两个点。

若令：

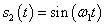
则傅里叶变换是：

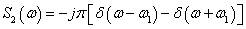
在matlab中执行以下命令：

则可得其频谱，如图2所示：

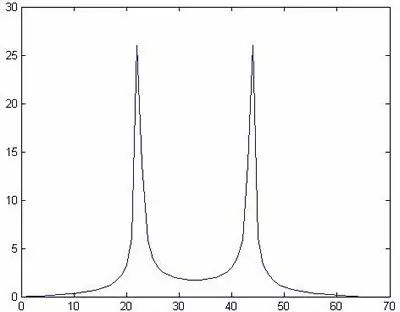
图2

由图可得两个峰值的位置基本与图1相同，这由其傅里叶表达式也可以得出此结论。

以上分别说明了余弦和正弦的频谱，而且余弦和正弦均是实数序列，实数序列的离散傅里叶变换(DFT)具有共轭对称性质（此性质可百度或查阅数字信号处理相关书籍或自行推导，很简单的），这从图中也可以看出。（画图时取其模值，共轭取模与原先数取模将变成相等）

二、复数的频谱

若令

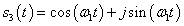
则计算其傅里叶变换可得：

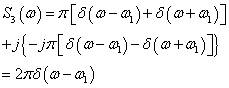
因此频谱中将只有一根谱线。在matlab中输入以下命令：

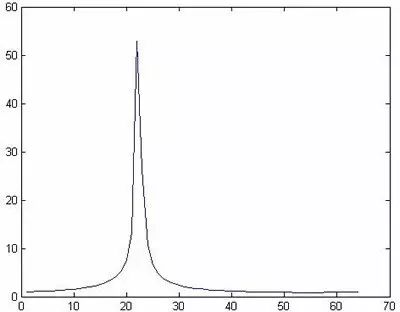
图3

从图3可以看出，对于一个复数序列求频谱，它的幅度谱将不再是对称的两根谱线。其实经过类似于实数序列的推导可以得出，复数序列的频谱将不再具有类似于实数序列的共轭对称性质。

当ω1为负值时会如何呢？同样对于信号：

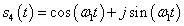
输入以下命令计算它的频谱：

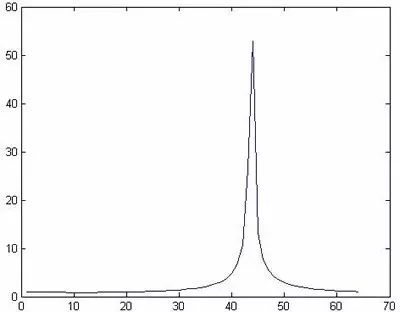
图4

对比图3和图4可知，当频率为正值时，峰值将在1 ~ 32范围内；而当频率为负值时，峰值将在33 ~ 64之间。此性质可通俗的描述如下：

对于信号：

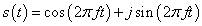
对其进行符合奈奎斯特采样定理的采样，设采样率为fs，采样点数为N，得到数字信号s(n)，n = [0,…,N-1]，则对s(n)做DFT变换进行谱分析后得到S(k)，k = [0,…,N-1]。观察S(k)的幅度谱，若k = 0 ~ N/2-1之间有峰值，则s(t)的频率f在0 ~ fs/2之间；若k =N/2 ~ N-1之间有峰值，则s(t)的频率f在-fs/2 ~ 0之间；并且有且只有一个峰值。

设幅度谱峰值当k = k1时出现，则s(t)的频率为：

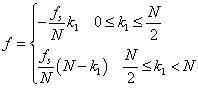
三、频率分辨率

频率分辩率是指频域取样中两相邻点间的频率间隔。更确切的说是如果某一信号含有两个频率成分f1和f2，Of = |f2-f1|，频率分辨率的概念是如果频率分辨率大于Of，对信号进行谱分析后将不能视别出其含有两个频率成分，这两个频率将混叠在一起。

以下是摘自华科姚天任《数字信号处理（第二版）》第92页的一段：

现在我们设定信号：

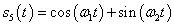
其中ω1=2π×1000，ω2=2π×1100，在matlab中输入以下命令计算其频谱：

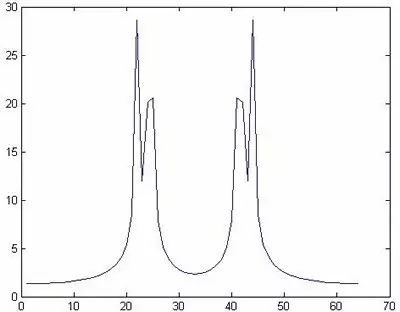
图5

从图5中可以看出能够分辨出f1 = 1000Hz和f2 = 1100Hz两个频率分量。我们利用上面的理论来计算一下此时的频率分辨率：

• 采样频率fs = 3000Hz

• 采样点个数N = 64
  

• 最长记录长度tp = N×(1/fs)

• 频率分辨率F = 1/tp = fs/N = 3000/64 =46.875Hz

因为F < f2-f1 = 100Hz，因此能够分辨出两个频率分量。下面我们作如下尝试：

第一种尝试：fs不变仍为3000Hz，即奈奎斯特定理仍然满足，大于信号s5(t)的最高频率分量1100Hz的两倍，但将采样点个数N减小为24个，在matlab中输入以下命令：

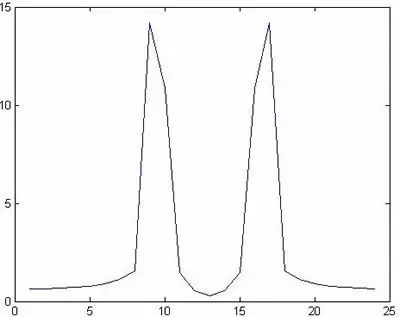
图6

第二种尝试：采样率fs升为8000Hz，即满足奈奎斯特采样定理，大于信号s5(t)的最高频率分量1100Hz的两倍，采样点个数N不变，仍为64个，在matlab中输入以下命令：

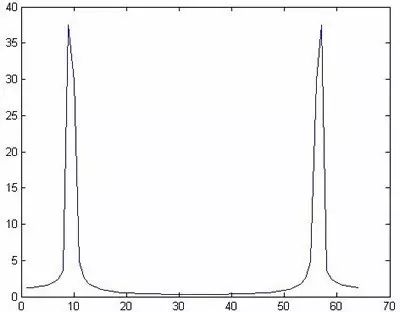
图7

由图6和图7可以看出，这两种尝试虽然满足奈奎斯特采样定理，但都不能分辨出两个频率分量，用前面的理论知识可以作如下分析：

第一种尝试的频率分辨率：

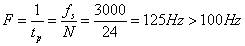
第二种尝试的频率分辨率：

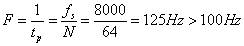
因此以上两种尝试均不能分辨出频率间隔为100Hz的两个频率分量。

四、高密度谱的概念

如图6所示，频谱很不平滑，呈很明显的折线状态，我们在matlab中输入以下命令：

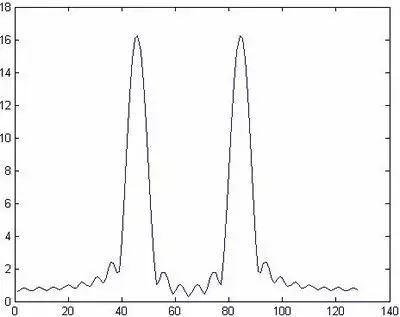
图8

图8是将图6中的信号在时域补了104个零后才进行谱分析的。比较图6与图8，虽然相对于图6来说图8的频率分辨率并没有增加，但其每个点所代表的频率更小了，也就是密度更高了（同样3000Hz的频率，图6中使用了24点，而图8中使用了128点），这就是高密度谱。

通常可以靠补零的方式来提高频谱的密度，但补零不能提高频率分辨率。很多人在此很迷惑，在末尾加零后，使一个周期内的点数增加，必然使样点间隔更近，谱线更密，是以前看不到的谱分量就可以看到了，能够看到更多的谱，不是提高分辨力了吗？

其实加零后，并没有改变原有记录的数据，原有数据的频谱一开始就存在，我们只是有的看不见，加零后只是让我们看见原来本就存在的频率，也就是说，原始数据代表的该有的频率就有，没有的频率加再多的零（极限是成连续的），也没法看见。

在数字信号处理中，高分辨率谱和高密度谱是较为易混淆的两个概念。获得高分辨率谱的途径是增加信号采样的记录时间tp，而高密度谱则是通过在时域补零得到的。高分辨谱的用途很显示，可以分辨出频率间隔更小的两个频率分量，那么高分辨率谱有什么作用呢？

要想明白高密度谱的概念，就不得知道一个名词：栅栏效应。高分辨率谱就是为了减小栅栏效效的。实际信号是无限长的，其频谱是连续的，但是要用计算机对信号进行频谱分析，就必须把它截短使之成为有限长度为tp的信号，这样的截短相当于对信号加矩形窗。

经过加窗截取，信号的周期变为tp，其频谱相应地由原来的连续谱变为离散谱，离散谱的谱线只在f = 1/tp的整数倍的位置上才出现，于是谱线间的实际信号的谱线有可能被挡住而损失掉，这称之为栅栏效应。例如截取信号长度为tp=0.5s，则可得到的谱线为2Hz，4Hz，6Hz，8Hz，…，若信号中包含频率为7Hz的分量，则该分量将被栅栏挡住，无法显示出来。

参考文献：

• 姚天任.数字信号处理(第二版)[M].华中科技大学出版社，2000.
  

  
  

• 万灵达.基于FFT的高精度频率估计算法研究[D].西安电子科技大学，2010.

  
  

• 其它网络资源.

原文链接：http://blog.csdn.net/jbb0523/article/details/7283847

#推荐阅读#

• 一位老电子工程师的十年职场感悟
  

• “Y电容”到底放哪个位置更好？

• u-boot和bootloader的区别

• 一颗芯片的从无到有
  

• USB 接口电路设计常见问题

• 画好原理图的技巧
  

• 完美通俗解读小波变换，终于懂了小波是什么

• 电流检测电路
  

• Altium Design PCB拼板完整教程

• 怎么办？单片机固件又被人破解了~~
  

• 示波器接地良好，反而容易炸机？

• 数学之美：谈Smith圆图

• 硬件知识“三重奏”