信号分析之：信号处理中的“平均”

面包板社区 2021-09-24 19:53

TI MCU方案：电动汽车实时控制 【应用手册】TI 全新MCU及C29内核的电动汽车应用方案

在实际的测量中，通常是在有明显噪声的情况下测量所需信号。更有甚者，想要测试的真实信号会淹没在噪声中，有点像噪音的示例包括语音、音乐、地震数据等。根据以上条件，在进行FFT分析时，必须满足可以在有背景噪声的情况下，准确的测出所需的信号。

在统计学中，提高对某个测量值准确性的方法是平均 (Average)。在处理一个信号结果时，通常就会让数据分析系统进行平均处理，本文主要阐述两种平均方式：RMS平均（能量平均）和线性平均。

RMS平均

当我们在观察频谱，并尝试猜测频谱分量的平均值时，这其实是一个粗略的估计RMS平均值的过程。因为此时估计的信号平均幅度，是没有任何相位差信息的。这种平均方式对于确定动态信号的平均功率非常适合，获取的平均值越多，对能量水平的估计准确性就越好。

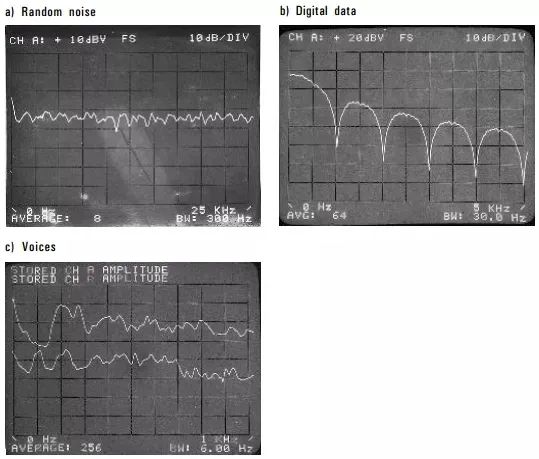
上图分别展示了随机噪声，数字信号和人声的RMS平均频谱。这些示例中的每一个都是一个相当随机的过程，但是平均下来，我们可以看到其频谱的基本规律趋势。

如果我们想在存在噪声的情况下测量一个小的信号，RMS平均这种方式将为我们提供信号加噪声的良好估计结果，但是无法提高信噪比，因此只能对总信号及噪声/信号能量进行更准确的估算。

线性平均

基于上述平均方式，其实存在一种用于提高测量信噪比的技术，称为线性平均。

线性平均可以通过多种方式实现，但比较容易理解的是在时域中进行平均。在这种情况下，同步信号用于触发进行记录。因此，在我们每次记录时，输入的周期部分将始终完全相同，而噪声会变化。如果我们将一系列触发信号记录加在一起，然后除以我们已获取的记录数，便可以计算出所谓的线性平均值。

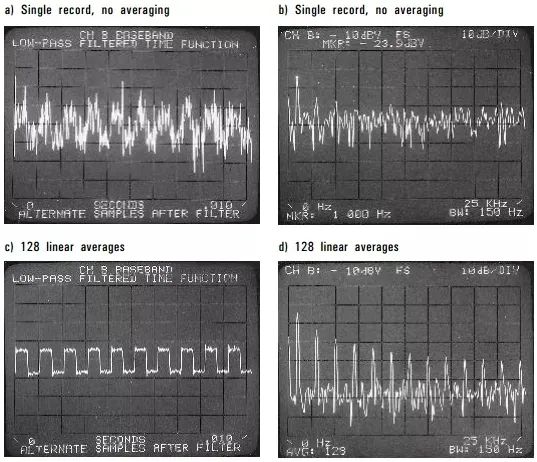
由于周期信号将在每个时间记录中精确地重复自身，因此可以平均到其精确值。但是由于每个时间记录中的噪声都不同，因此其趋向于平均为零。我们取的平均值越多，噪声越接近零，便可以继续提高测量的信噪比。上图a展示了淹没在噪声中的方波的时间记录。图c中是经过128次平均后得到的结果，信噪比有了显著提高。将这两个结果都转换到频域 (b、d) 中，可以看出由于降低了本底噪声，现在能够精确地测量出方波信号中对应的谐波数量。

来源：吉兴汽车声学部件科技有限公司微信公众号（ID：gh_ff1a461c24cb），作者：陈晓君。