前言:姗姗来迟,终于推出了自己的第一篇文章。大家好,允许再次自我介绍一下:公众号“转子磁场定向”(知乎号同名,微信PMSM_RFO),毕业以来一直在深圳从事电机控制相关工作已十余年。涉及产品包括变频器、伺服、家电控制器、电动工具。做过永磁同步电机PMSM和感应电机ACIM。来到微信平台,希望分享自己的优质内容,和志同道合的朋友共同探讨。
简介:高频注入在国外已研究了很多年,国内的论文也不少,但是国内能够应用到产品的公司寥寥无几。本文采用全新的视角,推出一种已经量产,并且可以在IPM零速输出转矩的控制方法。SPM可以低速使用,无法零速使用。伺服因为转矩脉动和控制精度要求无法使用该方法。
饱和凸极性
谈到高频注入,大家第一步会联想到凸极性。内埋式IPM具有结构凸极,表贴式SPM具有饱和凸极。首先弄清楚什么是SPM的饱和凸极?
直轴磁路的 曲线如下图一所示:
对于SPM,不考虑转子磁场, 。当电流矢量与 轴正向重合,那么电流矢量的磁场和转子磁场叠加,就会导致直轴磁路出现饱和;当电流矢量与 轴反向重合,那么激励磁场与转子磁场抵消,磁路处于线性段。如定义 为直轴正向电感, 为直轴负向电感,那么 ,这就是SPM的饱和凸极性。饱和凸极性可用于低速控制方法,也可以用于初始位置检测。
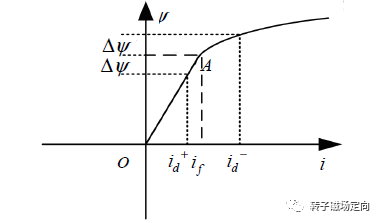
图1 直流磁路磁链-电流曲线
如图二所示:当给定子绕组施加激励,电流矢量与 轴磁场的相互作用决定了 轴电感是变化的。当激励电流与 轴正交时, 最大,电感变化曲线与电流夹角基本是一个接近正弦的关系。
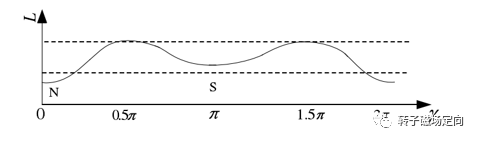
图2 SPM电感变化曲线
介绍了饱和凸极性,就得思考一个问题。常用的高频注入三大流派:旋转高频注入、脉振、方波高频注入。后两者不分SPM和IPM,旋转高频注入只能用于IPM。三种方法的增益都有 ,为什么单单旋转高频注入不能用在SPM呢?
这个问题暂时没有看到公开的解释,谈下自己的理解,不一定对。
脉振和方波高频注入,都是在 轴上施加电流激励。假设 轴电流激励和 轴相同,那么因为 轴还有转子磁场,和电流激励相互作用,因为正向饱和效应和反向消磁,就会造成 轴的磁路和 轴肯定不同,也就是说很大的概率会导致 ,所以高频注入增益不为0。
对于旋转高频注入,在 静止坐标系注入旋转激励矢量,与 轴的位置是无关的,二者相对位置随机。那么对于SPM,很有可能在某些时刻电流激励全部施加在 轴上,造成 轴磁路和 轴磁路工作在相同的情况,这样的结果就是很大概率 ,高频注入增益为0,提取误差信号失败。
所以旋转高频注入只能在强凸极性的IPM使用,无论磁路如何饱和,都不会出现交直轴电感相等的情况。脉振和方波高频注入,利用饱和凸极性,也可以用在SPM的低速控制和初始位置辨识。
控制方法
上文提到,旋转高频注入和脉振精度高,被研究的也很多,计算比较复杂,需要用到BSF,SFF,BPF,PLL等滤波器。二者控制框图如下:
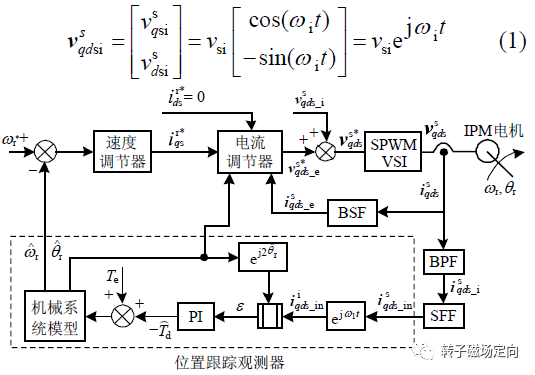
图3 旋转高频注入控制框图
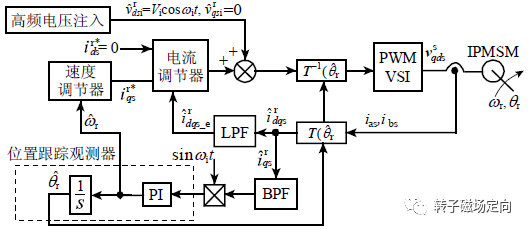
图4 脉振高频注入控制框图
二者施加的电压激励都是正弦波连续信号 ,需要过零点,容易常用的受到死区补偿等逆变器非线性因素的影响。比如说,施加的激励大约是标幺值0.01,因为死区的存在不可避免需要死区补偿。死区补偿的误差就会导致输出参考是0.01,实际的输出可以偏差很大,最终导致计算时误差较大。
死区补偿在实际的产品中,想做好没有那么简单,很多因素比如大功率的IGBT开关延时,IGBT管压降的影响,是仿真和理论无法体现的。以后有空再介绍。
为了规避死区补偿相关非线性因素的影响,采用方波注入是最好的方式。因为注入的方波是一个类似开关的离散信号,不需要过零点。只有正负和零三种状态,幅值很大,低速下叠加在基波上,输出电压幅值也较大,不用担心非线性因素造成的误差。
比如220VAC的电机,当速度较低时,输出电压较低,只有10V以下,加上脉振或者正弦波信号处于过零点附近时,整体输出电压幅值低。该工况下死区占输出电压比例较大,当死区补偿出现误差时就会导致实际输出电压与参考不符,降低计算精度。
如果采用方波注入的方式,一般方波幅值都在额定电压20%以上。假设注入50V的方波,叠加在10V的基波上,输出幅值幅值在50V以上,这种情况下死区补或者不补,已经不重要了,实际输出电压和参考的误差可以忽略。
当注入高频激励,因为脉宽较窄,远低于机械时间常数,所以反电势和定子压降忽略。电压方程表示为:
在第一个开关周期,给 轴施加正向激励 ,第二个开关周期,给 轴施加负向激励 。电流会先上升,后下降。因为磁滞回线的影响,无法保证两个开关周期后电流绝对回到零点,所以会再等待一个开关周期,激励为0,等电流回零。三个开关周期为一个完整的激励周期:
方波电压激励和脉冲电流波形如下图:
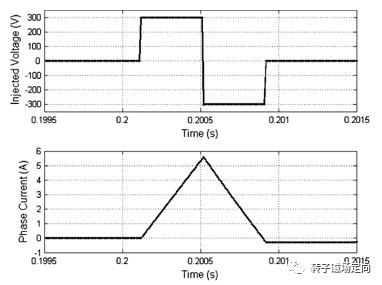
图5 方波电压和脉冲电流
真实坐标系, 是估算坐标系,定义估算误差: 。坐标系示意图如下:
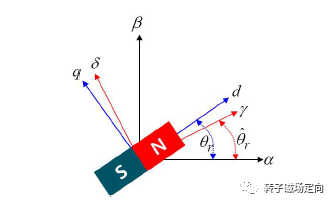
图6 估算坐标系和真实坐标系
定义 , ,结合上述公式推导出:
给估算坐标系施加高频方波激励 ,脉冲宽度为开关周期 ,得到脉冲响应电流:
估算坐标系 轴的电流响应为:
通过上式就得到了角度误差:
既然拿到了角度误差,直接给到锁相环PLL,就能输出角度和速度了,控制框图如下:
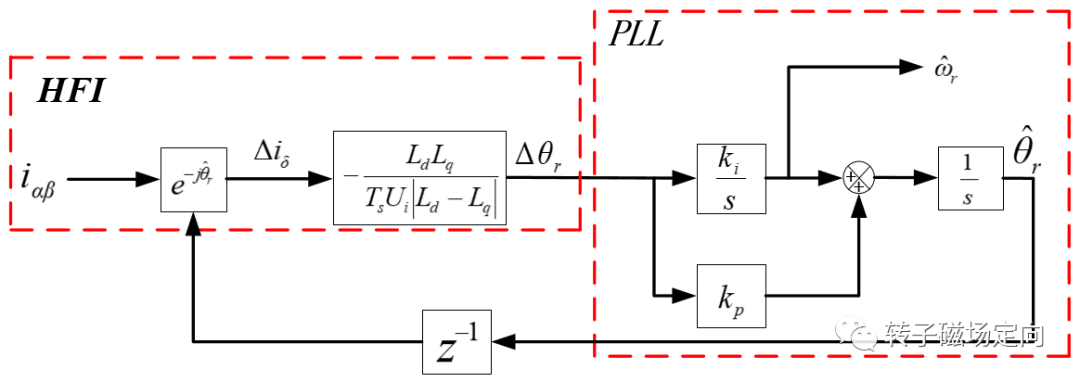
图7 高频方波注入控制框图
仿真波形
采用IPM仿真的参数如下:

图8 IPM电机参数
给定参考速度标幺值0.05,空载开机并且加50%阶跃负载。波形如下:
第一栏黄色是参考速度,蓝色是实际速度。因为加阶跃负载,所以电机会反转,速度环起作用后输出力矩会正转,并且跟上参考速度。
第二栏是真实角度,先正转,加载后反转再正转。
第三栏黄色是实际输出转矩,因为HFI的原因会带有脉动。蓝色是负载转矩。
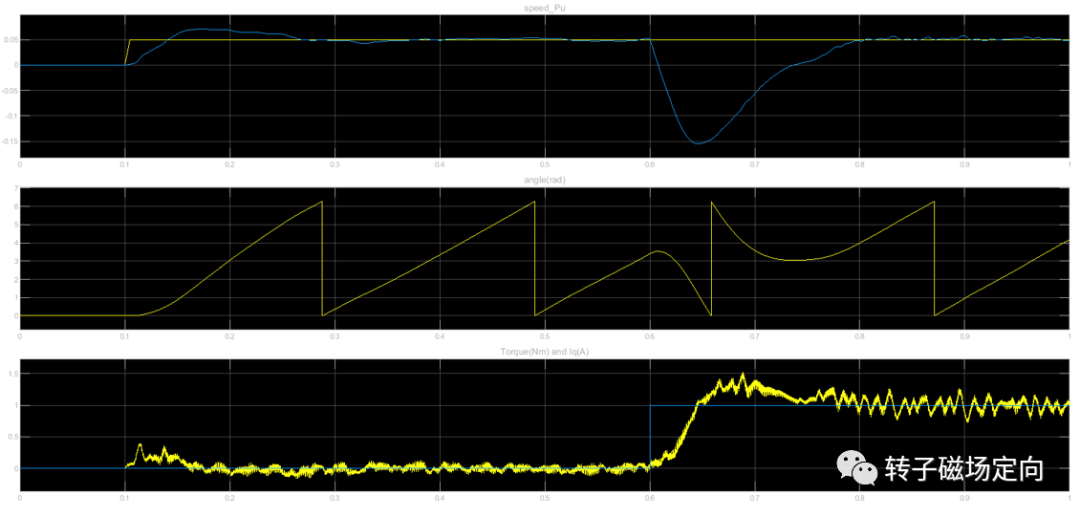
图9 低速突加载
在零速下突加50%阶跃负载,波形如下:
第一栏是参考速度和实际速度;第二栏可以看到稳定后角度不再波动,因为是零速;第三栏就是输出转矩和阶跃负载。
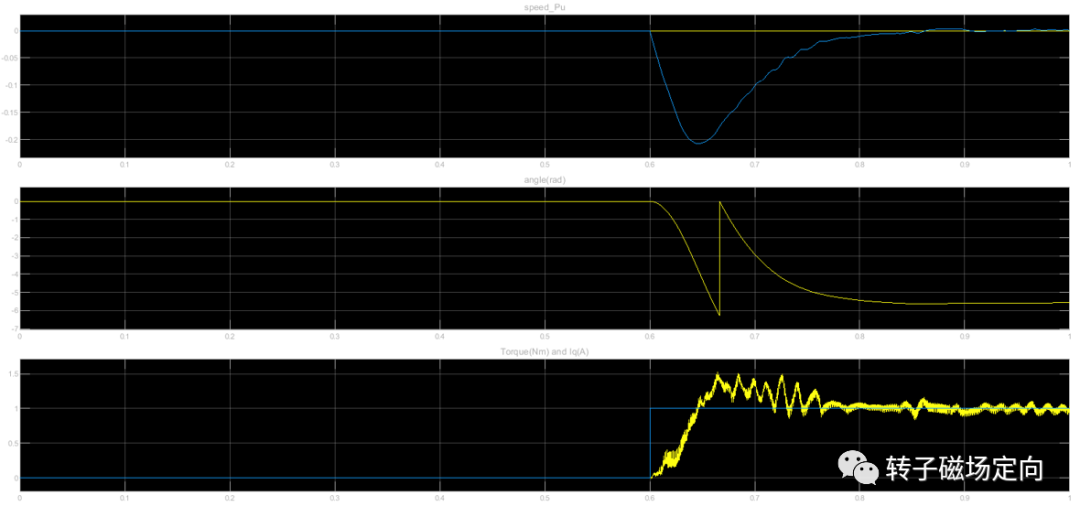
图10 零速带载
零速下的观测误差如下图,第一栏是实际角度和估算角度,第二栏和第三栏是估算误差,稳态误差不超过10degrees,动态误差不超过30degrees。
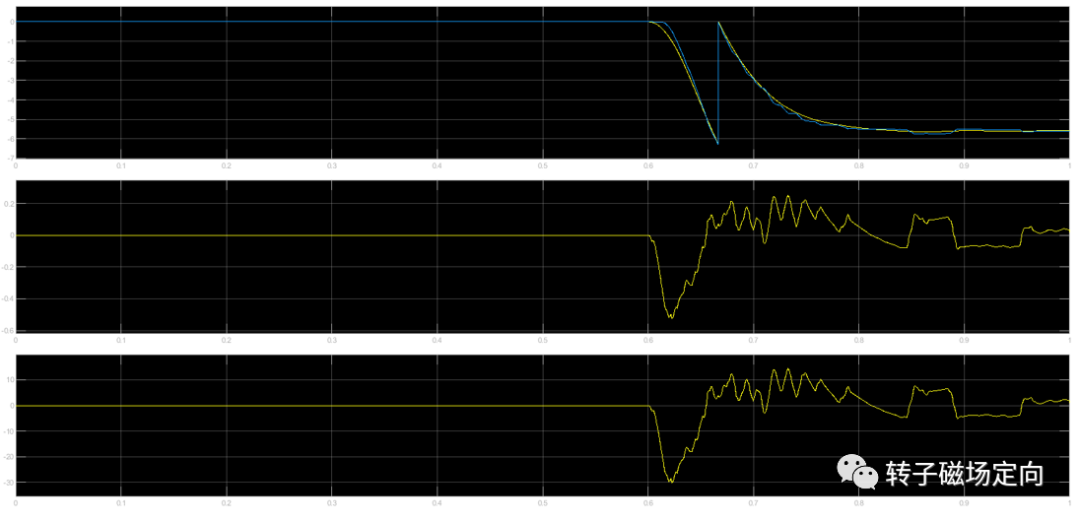
图11 零速下角度误差
电压脉冲波形和电流响应如下图,黄色是方波电压激励,蓝色是 轴脉冲电流响应,呈三角波状。橙色是 轴电流响应,基本为0,说明定向比较准确,脉冲激励施加到直轴,交轴上没有脉冲电流。波形是以标幺值为单位。
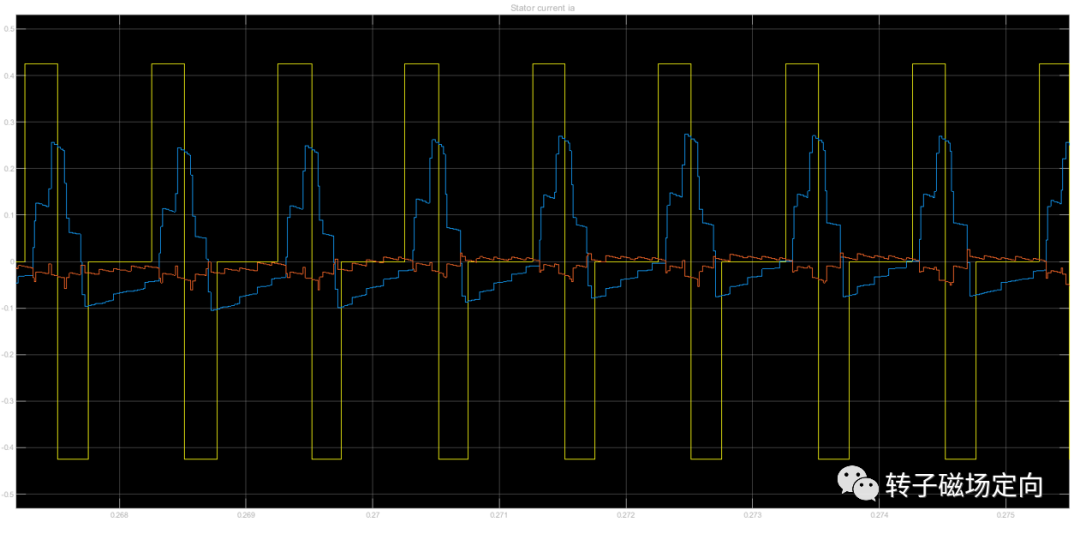
图12 方波电压和脉冲电流
高频注入相比其他低速带载观测器,对定子电阻不敏感。因为方法决定了定子电压压降可以去忽略,随温升的变大就不占主要作用。假设真实电阻比计算使用电阻大一倍, 相当于 。测试5%带载仍然能正常工作,验证HFI对定子电阻的不敏感性。
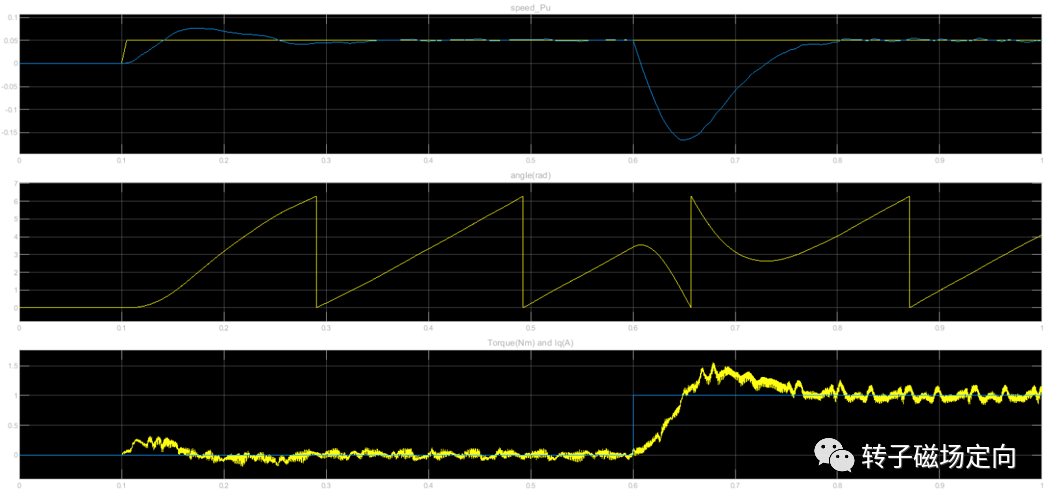
图13 HFI对定子电阻不敏感
实验波形
因为工作保密关系,不方便贴出视频。上传380V,22kW的IPM在低速2Hz切载的波形,使用HFI控制方法,从70%额定负载大约30A有效值切换到150%额定负载约70A有效值,没有失步,切换平滑,动态响应好。从波形中可以看出,因为使用了HFI,所以电流波形含有大量的谐波。
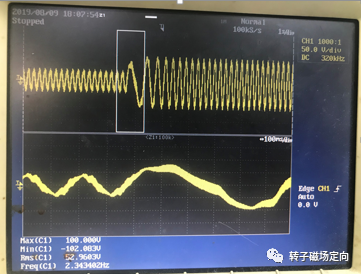
图14 IPM使用HFI低速从70%负载切换到150%负载
在IPM上,是可以在零速下输出50%以上额定转矩的,很可惜目前手上没有波形~~~
总结
HFI优点包括:
1、信噪比高,注入高幅值的方波电压,产生高幅值的脉冲电流,对死区等非线性因素不敏感;
2、计算简单。没有SFF等滤波器,只需要合理设计PLL的带宽即可得到准确的观测器,设计简单。
3、带载能力强,IPM零速可以输出50%以上额定转矩,动态响应好,稳态精度高。
4、精度高。30rpm参考速度下,带满载速度误差低于+/-1rpm。
缺点:
噪音大;产生轻微的转矩脉动;转起来不难,量产的话对开发者要求较高;降低电机效率。
要实现量产,需要注意以下问题:
1、参数饱和问题。SPM也可以应用HFI,只是过载能力不如IPM,因为随着负载加大,电感饱和加剧,凸极性会降低。与电机还有实际负载,参数辨识都有关系。如何处理考验开发者能力。
2、参数辨识问题。对于 和 需要进行离线辨识,不能使用电桥测试。辨识精度直接决定了观测精度。
3、采样问题。桥臂采样实现有一定难度,在输出侧会更方便,对PWM配置也很关键。
4、方波电压幅值和脉宽如何选取,很考验开发者的能力。
5、高开关频率如何做。高低开关频率如何兼容也是一个难题。
6、PLL设计和带宽问题。PLL的比例和积分增益是有相互关系的,需要结合Matlab选定。
这篇HFI文章,我个人自信是目前为止公开的最专业详细的参考。如果觉得不错,请点个赞,多多转发。
因为是团队的成果,涉及到项目保密,细节不方便透露太多,相信这篇文章对大家有所帮助。如想了解进一步细节请私信或者添加微信PMSM_RFO,谢谢理解。
本期文章在同名知乎号“转子磁场定向”同步转载。
下一期文章各位朋友想看哪方面的设计,比如反电势模型、弱磁、初始位置辨识、异步电机、伺服或者其他热点问题,欢迎留言。