好快的时间,小米都10周年了。这次10周年照例也是一次营销,雷军看来是爱上演讲这样的方式了,以时间轴为中心,娓娓道来其中的事情。这次重点其实说的是,自己冲击第一的决心,大笔墨的着色了港股上市和美国的封锁。这些大家都可以去看(我就看了他写的演讲稿,没有看视频)。在演讲会的末尾,走出了一条“狗”,简单的做了一些动作,没有太敢修就又牵回去了。估计是怕小爱那样的出丑,或者是本身就做到这里了。雷军给它起名为钢蛋。很多人觉得CyberDog就是钢蛋的意思,事实上不是。

gif图,主要看传感器的布局
是网络狗的意思
今天就和我研究一下这条狗的相关,怎么说呢。每家媒体都在报道,但是稿子千篇一律,连洗稿都懒的洗。我写的话,就是又臭又长的“水文”了。
首先主控是NVIDIA JETSON XAVIER NX:
https://www.nvidia.cn/autonomous-machines/embedded-systems/jetson-xavier-nx/
就是这个样子的一个机器,也是边缘AI平台里面最贵的型号
我不知道自动驾驶的平台算吗?估计不算
| Jetson Nano 硬件情况探查 |
| NVIDIA Jetson nano I2C连接+网线SSH直连+smaba配置 |
| NVIDIA Jetson nano安装Jtop(资源监控) |
| NVIDIA Jetson nano安装GPIO安装 |
| NVIDIA Jetson nano安装I2C屏幕(ssd1306主控).上 |
| NVIDIA Jetson nano环境配置上 |
| jetson NanoCamera(使用) |
| 解决jetson Nano中python版本问题(Ubuntu系统都适用) |
| jetson Nano安装pycuda(编译安装版) |
| NVIDIA Jetson:实现一切自主的 AI 平台.1 |
其实都是一样的东西,我写了几十篇的Nano文章了,可以参考的看

板载核心
Jetson Xavier NX最多可提供21个TOPS,非常适合嵌入式和边缘系统中的高性能计算和AI。您可以获得384个NVIDIA CUDA® Cores,48个Tensor Cores,6个Carmel ARM CPU和两个NVIDIA深度学习加速器(NVDLA)引擎的性能。这些功能与超过51GB / s的内存带宽,视频编码和解码相结合,使Jetson Xavier NX成为并行运行多个现代神经网络并同时处理来自多个传感器的高分辨率数据的首选平台。

机器人适合在这些的地方部署
这里插一句机器狗,并不是自研,而是基于MIT Mini Cheetah和ROS 2的开源平台。
https://github.com/search?q=MIT+Mini+Cheetah你去探索这里
https://github.com/Derek-TH-Wang/quadruped_ctrl如果你买不起狗(我买不起,说的就是我)
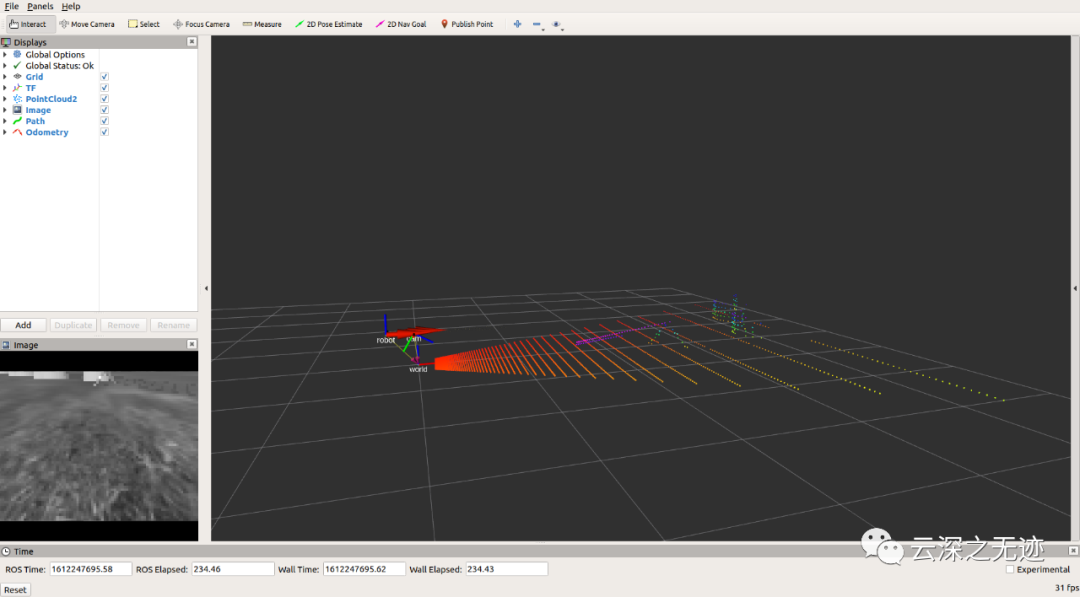
你可在虚拟环境内进行仿真操作

就这样,想摸摸
https://github.com/sevocrear/Mini-Cheetah-ROS一个ROS的包
https://github.com/wei1224hf/RuFengRobot另一个库,包含大量的资料。保证你可以生产机械狗

里面有大量的机械结构图纸
import numpy as npimport matplotlib.pyplot as pltimport matplotlib.animation as animationfrom matplotlib.widgets import Slider, Button#plt.rcParams['animation.ffmpeg_path'] = 'D:/portableSoftware/ShareX/ShareX/Tools/ffmpeg.exe'interval = 50 # ms, time between animation framesfig, ax = plt.subplots(figsize=(6, 6))plt.subplots_adjust(left=0.15, bottom=0.35)ax.set_aspect('equal')plt.xlim(-1.4*40, 1.4*40)plt.ylim(-1.4*40, 1.4*40)# plt.grid()t = np.linspace(0, 2*np.pi, 400)delta = 1e = 2n = 10RD = 40rd = 5# plt.grid()# draw pinl0, = ax.plot([], [], 'k-', lw=2)l1, = ax.plot([], [], 'k-', lw=2)l2, = ax.plot([], [], 'k-', lw=2)l3, = ax.plot([], [], 'k-', lw=2)l4, = ax.plot([], [], 'k-', lw=2)l5, = ax.plot([], [], 'k-', lw=2)l6, = ax.plot([], [], 'k-', lw=2)l7, = ax.plot([], [], 'k-', lw=2)l8, = ax.plot([], [], 'k-', lw=2)l9, = ax.plot([], [], 'k-', lw=2)l10, = ax.plot([], [], 'k-', lw=2)l11, = ax.plot([], [], 'k-', lw=2)l12, = ax.plot([], [], 'k-', lw=2)l13, = ax.plot([], [], 'k-', lw=2)l14, = ax.plot([], [], 'k-', lw=2)l15, = ax.plot([], [], 'k-', lw=2)l16, = ax.plot([], [], 'k-', lw=2)l17, = ax.plot([], [], 'k-', lw=2)l18, = ax.plot([], [], 'k-', lw=2)l19, = ax.plot([], [], 'k-', lw=2)l20, = ax.plot([], [], 'k-', lw=2)l21, = ax.plot([], [], 'k-', lw=2)l22, = ax.plot([], [], 'k-', lw=2)l23, = ax.plot([], [], 'k-', lw=2)l24, = ax.plot([], [], 'k-', lw=2)l25, = ax.plot([], [], 'k-', lw=2)l26, = ax.plot([], [], 'k-', lw=2)l27, = ax.plot([], [], 'k-', lw=2)l28, = ax.plot([], [], 'k-', lw=2)l29, = ax.plot([], [], 'k-', lw=2)l30, = ax.plot([], [], 'k-', lw=2)l31, = ax.plot([], [], 'k-', lw=2)l32, = ax.plot([], [], 'k-', lw=2)l33, = ax.plot([], [], 'k-', lw=2)l34, = ax.plot([], [], 'k-', lw=2)l35, = ax.plot([], [], 'k-', lw=2)l36, = ax.plot([], [], 'k-', lw=2)l37, = ax.plot([], [], 'k-', lw=2)l38, = ax.plot([], [], 'k-', lw=2)l39, = ax.plot([], [], 'k-', lw=2)l40, = ax.plot([], [], 'k-', lw=2)for i in range(int(10)):x = (5*np.sin(t) + 40*np.cos(2*i*np.pi/10))y = (5*np.cos(t) + 40*np.sin(2*i*np.pi/10))if i == 0:l0, = ax.plot(x, y, 'k-')if i == 1:l1, = ax.plot(x, y, 'k-')if i == 2:l2, = ax.plot(x, y, 'k-')if i == 3:l3, = ax.plot(x, y, 'k-')if i == 4:l4, = ax.plot(x, y, 'k-')if i == 5:l5, = ax.plot(x, y, 'k-')if i == 6:l6, = ax.plot(x, y, 'k-')if i == 7:l7, = ax.plot(x, y, 'k-')if i == 8:l8, = ax.plot(x, y, 'k-')if i == 9:l9, = ax.plot(x, y, 'k-')if i == 10:l10, = ax.plot(x, y, 'k-')if i == 11:l11, = ax.plot(x, y, 'k-')if i == 12:l12, = ax.plot(x, y, 'k-')if i == 13:l13, = ax.plot(x, y, 'k-')if i == 14:l14, = ax.plot(x, y, 'k-')if i == 15:l15, = ax.plot(x, y, 'k-')if i == 16:l16, = ax.plot(x, y, 'k-')if i == 17:l17, = ax.plot(x, y, 'k-')if i == 18:l18, = ax.plot(x, y, 'k-')if i == 19:l19, = ax.plot(x, y, 'k-')if i == 20:l20, = ax.plot(x, y, 'k-')if i == 21:l21, = ax.plot(x, y, 'k-')if i == 22:l22, = ax.plot(x, y, 'k-')if i == 23:l23, = ax.plot(x, y, 'k-')if i == 24:l24, = ax.plot(x, y, 'k-')if i == 25:l25, = ax.plot(x, y, 'k-')if i == 26:l26, = ax.plot(x, y, 'k-')if i == 27:l27, = ax.plot(x, y, 'k-')if i == 28:l28, = ax.plot(x, y, 'k-')if i == 29:l29, = ax.plot(x, y, 'k-')if i == 30:l30, = ax.plot(x, y, 'k-')if i == 31:l31, = ax.plot(x, y, 'k-')if i == 32:l32, = ax.plot(x, y, 'k-')if i == 33:l33, = ax.plot(x, y, 'k-')if i == 34:l34, = ax.plot(x, y, 'k-')if i == 35:l35, = ax.plot(x, y, 'k-')if i == 36:l36, = ax.plot(x, y, 'k-')if i == 37:l37, = ax.plot(x, y, 'k-')if i == 38:l38, = ax.plot(x, y, 'k-')if i == 39:l39, = ax.plot(x, y, 'k-')if i == 40:l40, = ax.plot(x, y, 'k-')def draw_pin_init():l0.set_data([0], [0])l1.set_data([0], [0])l2.set_data([0], [0])l3.set_data([0], [0])l4.set_data([0], [0])l5.set_data([0], [0])l6.set_data([0], [0])l7.set_data([0], [0])l8.set_data([0], [0])l9.set_data([0], [0])l10.set_data([0], [0])l11.set_data([0], [0])l12.set_data([0], [0])l13.set_data([0], [0])l14.set_data([0], [0])l15.set_data([0], [0])l16.set_data([0], [0])l17.set_data([0], [0])l18.set_data([0], [0])l19.set_data([0], [0])l20.set_data([0], [0])l21.set_data([0], [0])l22.set_data([0], [0])l23.set_data([0], [0])l24.set_data([0], [0])l25.set_data([0], [0])l26.set_data([0], [0])l27.set_data([0], [0])l28.set_data([0], [0])l29.set_data([0], [0])l30.set_data([0], [0])l31.set_data([0], [0])l32.set_data([0], [0])l33.set_data([0], [0])l34.set_data([0], [0])l35.set_data([0], [0])l36.set_data([0], [0])l37.set_data([0], [0])l38.set_data([0], [0])l39.set_data([0], [0])l40.set_data([0], [0])def draw_inner_pin_init():p0.set_data([0], [0])p1.set_data([0], [0])p2.set_data([0], [0])p3.set_data([0], [0])p4.set_data([0], [0])p5.set_data([0], [0])p6.set_data([0], [0])p7.set_data([0], [0])p8.set_data([0], [0])p9.set_data([0], [0])def pin_update(n, d, D):for i in range(int(n)):x = (d/2*np.sin(t) + D/2*np.cos(2*i*np.pi/n))y = (d/2*np.cos(t) + D/2*np.sin(2*i*np.pi/n))if i == 0:l0.set_data(x, y)if i == 1:l1.set_data(x, y)if i == 2:l2.set_data(x, y)if i == 3:l3.set_data(x, y)if i == 4:l4.set_data(x, y)if i == 5:l5.set_data(x, y)if i == 6:l6.set_data(x, y)if i == 7:l7.set_data(x, y)if i == 8:l8.set_data(x, y)if i == 9:l9.set_data(x, y)if i == 10:l10.set_data(x, y)if i == 11:l11.set_data(x, y)if i == 12:l12.set_data(x, y)if i == 13:l13.set_data(x, y)if i == 14:l14.set_data(x, y)if i == 15:l15.set_data(x, y)if i == 16:l16.set_data(x, y)if i == 17:l17.set_data(x, y)if i == 18:l18.set_data(x, y)if i == 19:l19.set_data(x, y)if i == 20:l20.set_data(x, y)if i == 21:l21.set_data(x, y)if i == 22:l22.set_data(x, y)if i == 23:l23.set_data(x, y)if i == 24:l24.set_data(x, y)if i == 25:l25.set_data(x, y)if i == 26:l26.set_data(x, y)if i == 27:l27.set_data(x, y)if i == 28:l28.set_data(x, y)if i == 29:l29.set_data(x, y)if i == 30:l30.set_data(x, y)if i == 31:l31.set_data(x, y)if i == 32:l32.set_data(x, y)if i == 133:l33.set_data(x, y)if i == 34:l34.set_data(x, y)if i == 35:l35.set_data(x, y)if i == 36:l36.set_data(x, y)if i == 37:l37.set_data(x, y)if i == 38:l38.set_data(x, y)if i == 39:l39.set_data(x, y)if i == 40:l40.set_data(x, y)def pin_update3(n, e, d, D, phi):for i in range(int(n)):x = (d/2*np.sin(t) + D/2*np.cos(2*i*np.pi/n))*np.cos(-phi/(n)) - \(d/2*np.cos(t) + D/2*np.sin(2*i*np.pi/n)) * \np.sin(-phi/(n)) + e*np.cos(phi)y = (d/2*np.sin(t) + D/2*np.cos(2*i*np.pi/n))*np.sin(-phi/(n)) + \(d/2*np.cos(t) + D/2*np.sin(2*i*np.pi/n)) * \np.cos(-phi/(n)) + e*np.sin(phi)if i == 0:l0.set_data(x, y)if i == 1:l1.set_data(x, y)if i == 2:l2.set_data(x, y)if i == 3:l3.set_data(x, y)if i == 4:l4.set_data(x, y)if i == 5:l5.set_data(x, y)if i == 6:l6.set_data(x, y)if i == 7:l7.set_data(x, y)if i == 8:l8.set_data(x, y)if i == 9:l9.set_data(x, y)if i == 10:l10.set_data(x, y)if i == 11:l11.set_data(x, y)if i == 12:l12.set_data(x, y)if i == 13:l13.set_data(x, y)if i == 14:l14.set_data(x, y)if i == 15:l15.set_data(x, y)if i == 16:l16.set_data(x, y)if i == 17:l17.set_data(x, y)if i == 18:l18.set_data(x, y)if i == 19:l19.set_data(x, y)if i == 20:l20.set_data(x, y)if i == 21:l21.set_data(x, y)if i == 22:l22.set_data(x, y)if i == 23:l23.set_data(x, y)if i == 24:l24.set_data(x, y)if i == 25:l25.set_data(x, y)if i == 26:l26.set_data(x, y)if i == 27:l27.set_data(x, y)if i == 28:l28.set_data(x, y)if i == 29:l29.set_data(x, y)if i == 30:l30.set_data(x, y)if i == 31:l31.set_data(x, y)if i == 32:l32.set_data(x, y)if i == 133:l33.set_data(x, y)if i == 34:l34.set_data(x, y)if i == 35:l35.set_data(x, y)if i == 36:l36.set_data(x, y)if i == 37:l37.set_data(x, y)if i == 38:l38.set_data(x, y)if i == 39:l39.set_data(x, y)if i == 40:l40.set_data(x, y)# draw inner_pinp0, = ax.plot([], [], 'g-', lw=2)p1, = ax.plot([], [], 'g-', lw=2)p2, = ax.plot([], [], 'g-', lw=2)p3, = ax.plot([], [], 'g-', lw=2)p4, = ax.plot([], [], 'g-', lw=2)p5, = ax.plot([], [], 'g-', lw=2)p6, = ax.plot([], [], 'g-', lw=2)p7, = ax.plot([], [], 'g-', lw=2)p8, = ax.plot([], [], 'g-', lw=2)p9, = ax.plot([], [], 'g-', lw=2)for i in range(int(6)):x = (5*np.sin(t) + 20*np.cos(2*i*np.pi/6))y = (5*np.cos(t) + 20*np.sin(2*i*np.pi/6))if i == 0:p0, = ax.plot(x, y, 'g-')if i == 1:p1, = ax.plot(x, y, 'g-')if i == 2:p2, = ax.plot(x, y, 'g-')if i == 3:p3, = ax.plot(x, y, 'g-')if i == 4:p4, = ax.plot(x, y, 'g-')if i == 5:p5, = ax.plot(x, y, 'g-')if i == 6:p6, = ax.plot(x, y, 'g-')if i == 7:p7, = ax.plot(x, y, 'g-')if i == 8:p8, = ax.plot(x, y, 'g-')if i == 9:p9, = ax.plot(x, y, 'g-')def inner_pin_update(n, N, rd, Rd, phi):for i in range(int(n)):x = (rd*np.sin(t) + Rd*np.cos(2*i*np.pi/n))*np.cos(-phi/(N-1)) - \(rd*np.cos(t) + Rd*np.sin(2*i*np.pi/n))*np.sin(-phi/(N-1))y = (rd*np.sin(t) + Rd*np.cos(2*i*np.pi/n))*np.sin(-phi/(N-1)) + \(rd*np.cos(t) + Rd*np.sin(2*i*np.pi/n))*np.cos(-phi/(N-1))if i == 0:p0.set_data(x, y)if i == 1:p1.set_data(x, y)if i == 2:p2.set_data(x, y)if i == 3:p3.set_data(x, y)if i == 4:p4.set_data(x, y)if i == 5:p5.set_data(x, y)if i == 6:p6.set_data(x, y)if i == 7:p7.set_data(x, y)if i == 8:p8.set_data(x, y)if i == 9:p9.set_data(x, y)# draw drive_pina = 5*np.sin(t)b = 5*np.cos(t)d0, = ax.plot(a, b, 'k-', lw=2)def drive_pin_update(r):x = r*np.sin(t)y = r*np.cos(t)d0.set_data(x, y)# inner circle:inner_circle1, = ax.plot([], [], 'r-', lw=2)inner_circle2, = ax.plot([], [], 'r-', lw=2)inner_circle3, = ax.plot([], [], 'r-', lw=2)inner_circle4, = ax.plot([], [], 'r-', lw=2)inner_circle5, = ax.plot([], [], 'r-', lw=2)inner_circle6, = ax.plot([], [], 'r-', lw=2)inner_circle7, = ax.plot([], [], 'r-', lw=2)inner_circle8, = ax.plot([], [], 'r-', lw=2)inner_circle9, = ax.plot([], [], 'r-', lw=2)inner_circle10, = ax.plot([], [], 'r-', lw=2)def draw_inner_circle_init():inner_circle10.set_data([0], [0])inner_circle1.set_data([0], [0])inner_circle2.set_data([0], [0])inner_circle3.set_data([0], [0])inner_circle4.set_data([0], [0])inner_circle5.set_data([0], [0])inner_circle6.set_data([0], [0])inner_circle7.set_data([0], [0])inner_circle8.set_data([0], [0])inner_circle9.set_data([0], [0])for i in range(6):x = (rd+e)*np.cos(t)+0.5*RD*np.cos(2*i*np.pi/6)+ey = (rd+e)*np.sin(t)+0.5*RD*np.sin(2*i*np.pi/6)if i == 0:inner_circle1, = ax.plot(x, y, 'r-')if i == 1:inner_circle2, = ax.plot(x, y, 'r-')if i == 2:inner_circle3, = ax.plot(x, y, 'r-')if i == 3:inner_circle4, = ax.plot(x, y, 'r-')if i == 4:inner_circle5, = ax.plot(x, y, 'r-')if i == 5:inner_circle6, = ax.plot(x, y, 'r-')if i == 6:inner_circle7, = ax.plot(x, y, 'r-')if i == 7:inner_circle8, = ax.plot(x, y, 'r-')if i == 8:inner_circle9, = ax.plot(x, y, 'r-')if i == 9:inner_circle10, = ax.plot(x, y, 'r-')def update_inner_circle(e, n, N, rd, Rd, phi):for i in range(int(n)):x = ((rd+e)*np.cos(t)+Rd*np.cos(2*i*np.pi/n))*np.cos(-phi/(N-1)) - ((rd+e)* np.sin(t)+Rd*np.sin(2*i*np.pi/n))*np.sin(-phi/(N-1)) + e*np.cos(phi)y = ((rd+e)*np.cos(t)+Rd*np.cos(2*i*np.pi/n))*np.sin(-phi/(N-1)) + ((rd+e)* np.sin(t)+Rd*np.sin(2*i*np.pi/n))*np.cos(-phi/(N-1)) + e*np.sin(phi)if i == 0:inner_circle1.set_data(x, y)if i == 1:inner_circle2.set_data(x, y)if i == 2:inner_circle3.set_data(x, y)if i == 3:inner_circle4.set_data(x, y)if i == 4:inner_circle5.set_data(x, y)if i == 5:inner_circle6.set_data(x, y)if i == 6:inner_circle7.set_data(x, y)if i == 7:inner_circle8.set_data(x, y)if i == 8:inner_circle9.set_data(x, y)if i == 9:inner_circle10.set_data(x, y)# inner pinA:x = (rd+e)*np.cos(t)+ey = (rd+e)*np.sin(t)inner_pinA, = ax.plot(x, y, 'r-')# driver line and dot:#self.line, = self.ax.plot([self.rd+self.e + self.e, 0],[0,0],'r-')dotA, = ax.plot([-rd - e - e], [0], 'ro', ms=5)def update_inner_pinA(e, Rm, phi):x = (Rm+e+e)*np.cos(t)+2*e*np.cos(phi)y = (Rm+e+e)*np.sin(t)+2*e*np.sin(phi)inner_pinA.set_data(x, y)x1 = (Rm+e+e)*np.cos(phi)+2*e*np.cos(phi)y1 = (Rm+e+e)*np.sin(phi)+2*e*np.sin(phi)# self.line.set_data([0,x1],[0,y1])dotA.set_data(x1, y1)# inner pinD:#x = (rd+e)*np.cos(t)-e#y = (rd+e)*np.sin(t)#inner_pinD, = ax.plot(x,y,'b-')# driver line and dot:#self.line, = self.ax.plot([self.rd+self.e + self.e, 0],[0,0],'r-')#dotD, = ax.plot([-rd- e- e],[0], 'bo', ms=5)# def update_inner_pinD(e,Rm, phi):# x = (Rm+e)*np.cos(t)-e*np.cos(phi)# y = (Rm+e)*np.sin(t)-e*np.sin(phi)# # inner_pinD.set_data(x,y)# x1 = (Rm+e)*np.cos(phi+np.pi)-e*np.cos(phi)# y1 = (Rm+e)*np.sin(phi+np.pi)-e*np.sin(phi)# self.line.set_data([0,x1],[0,y1])# dotD.set_data(x1, y1)# ehypocycloidA:rc = (n-1)*(RD/n)rm = (RD/n)xa = (rc+rm)*np.cos(t)-e*np.cos((rc+rm)/rm*t)ya = (rc+rm)*np.sin(t)-e*np.sin((rc+rm)/rm*t)dxa = (rc+rm)*(-np.sin(t)+(e/rm)*np.sin((rc+rm)/rm*t))dya = (rc+rm)*(np.cos(t)-(e/rm)*np.cos((rc+rm)/rm*t))x = xa + rd/np.sqrt(dxa**2 + dya**2)*(-dya) + 2*ey = ya + rd/np.sqrt(dxa**2 + dya**2)*dxaehypocycloidA, = ax.plot(x, y, 'r-')# driver line and dot: (rc+rm) - rd#self.eline, = self.ax.plot([(rc+rm) - rd, 0],[0,0],'r-')edotA, = ax.plot([(rc+rm) - rd], [0], 'ro', ms=5)def update_ehypocycloidA(e, n, D, d, phis):RD = D/2rd = d/2rc = (n-1)*(RD/n)rm = (RD/n)xa = (rc+rm)*np.cos(t)-e*np.cos((rc+rm)/rm*t)ya = (rc+rm)*np.sin(t)-e*np.sin((rc+rm)/rm*t)dxa = (rc+rm)*(-np.sin(t)+(e/rm)*np.sin((rc+rm)/rm*t))dya = (rc+rm)*(np.cos(t)-(e/rm)*np.cos((rc+rm)/rm*t))#x = (xa + rd/np.sqrt(dxa**2 + dya**2)*(-dya))*np.cos(phis/(n-1))-(ya + rd/np.sqrt(dxa**2 + dya**2)*dxa)*np.sin(phis/(n-1)) + e*np.cos(-phis) + e#y = (xa + rd/np.sqrt(dxa**2 + dya**2)*(-dya))*np.sin(phis/(n-1))+(ya + rd/np.sqrt(dxa**2 + dya**2)*dxa)*np.cos(phis/(n-1)) + e*np.sin(-phis)# ehypocycloidA.set_data(x,y)x = (xa + rd/np.sqrt(dxa**2 + dya**2)*(-dya))*np.cos(-2*phis/(n-1))-(ya +rd/np.sqrt(dxa**2 + dya**2)*dxa)*np.sin(-2*phis/(n-1)) + 2*e*np.cos(phis)y = (xa + rd/np.sqrt(dxa**2 + dya**2)*(-dya))*np.sin(-2*phis/(n-1))+(ya +rd/np.sqrt(dxa**2 + dya**2)*dxa)*np.cos(-2*phis/(n-1)) + 2*e*np.sin(phis)ehypocycloidA.set_data(x, y)# self.eline.set_data([e*np.cos(phis),x[0]],[e*np.sin(phis),y[0]])edotA.set_data(x[0], y[0])# ehypocycloidD:rc = (n+1)*(RD/n)rm = (RD/n)xa = (rc-rm)*np.cos(t)+e*np.cos((rc-rm)/rm*t)ya = (rc-rm)*np.sin(t)-e*np.sin((rc-rm)/rm*t)dxa = (rc-rm)*(-np.sin(t)-(e/rm)*np.sin((rc-rm)/rm*t))dya = (rc-rm)*(np.cos(t)-(e/rm)*np.cos((rc-rm)/rm*t))#x = xa - rd/np.sqrt(dxa**2 + dya**2)*(-dya) - e#y = ya - rd/np.sqrt(dxa**2 + dya**2)*dxax = xa - rd/np.sqrt(dxa**2 + dya**2)*(-dya)y = ya - rd/np.sqrt(dxa**2 + dya**2)*dxaehypocycloidD, = ax.plot(x, y, 'b-')# driver line and dot: (rc+rm) - rd#self.eline, = self.ax.plot([(rc+rm) - rd, 0],[0,0],'r-')edotD, = ax.plot([(rc+rm) - rd + e], [0], 'bo', ms=5)def update_ehypocycloidD(e, n, D, d, phis):RD = D/2rd = d/2rc = (n+1)*(RD/n)rm = (RD/n)xa = (rc-rm)*np.cos(t)+e*np.cos((rc-rm)/rm*t)ya = (rc-rm)*np.sin(t)-e*np.sin((rc-rm)/rm*t)dxa = (rc-rm)*(-np.sin(t)-(e/rm)*np.sin((rc-rm)/rm*t))dya = (rc-rm)*(np.cos(t)-(e/rm)*np.cos((rc-rm)/rm*t))x = (xa - rd/np.sqrt(dxa**2 + dya**2)*(-dya))y = (ya - rd/np.sqrt(dxa**2 + dya**2)*dxa)ehypocycloidD.set_data(x, y)# self.eline.set_data([e*np.cos(phis),x[0]],[e*np.sin(phis),y[0]])edotD.set_data(x[0], y[0])axcolor = 'lightgoldenrodyellow'ax_fm = plt.axes([0.25, 0.27, 0.5, 0.02], facecolor=axcolor)ax_Rm = plt.axes([0.25, 0.24, 0.5, 0.02], facecolor=axcolor)ax_n = plt.axes([0.25, 0.21, 0.5, 0.02], facecolor=axcolor)ax_Rd = plt.axes([0.25, 0.18, 0.5, 0.02], facecolor=axcolor)ax_rd = plt.axes([0.25, 0.15, 0.5, 0.02], facecolor=axcolor)ax_e = plt.axes([0.25, 0.12, 0.5, 0.02], facecolor=axcolor)ax_N = plt.axes([0.25, 0.09, 0.5, 0.02], facecolor=axcolor)ax_d = plt.axes([0.25, 0.06, 0.5, 0.02], facecolor=axcolor)ax_D = plt.axes([0.25, 0.03, 0.5, 0.02], facecolor=axcolor)sli_fm = Slider(ax_fm, 'fm', 10, 100, valinit=50, valstep=delta)sli_Rm = Slider(ax_Rm, 'Rm', 1, 10, valinit=5, valstep=delta)sli_n = Slider(ax_n, 'n', 3, 10, valinit=6, valstep=delta)sli_Rd = Slider(ax_Rd, 'Rd', 1, 40, valinit=20, valstep=delta)sli_rd = Slider(ax_rd, 'rd', 1, 10, valinit=5, valstep=delta)sli_e = Slider(ax_e, 'e', 0.1, 10, valinit=2, valstep=delta/10)sli_N = Slider(ax_N, 'N', 3, 40, valinit=10, valstep=delta)sli_d = Slider(ax_d, 'd', 2, 20, valinit=10, valstep=delta)sli_D = Slider(ax_D, 'D', 5, 100, valinit=80, valstep=delta)def update(val):sfm = sli_Rm.valsRm = sli_Rm.valsRd = sli_Rd.valsn = sli_n.valsrd = sli_rd.valse = sli_e.valsN = sli_N.valsd = sli_d.valsD = sli_D.valax.set_xlim(-1.4*0.5*sD, 1.4*0.5*sD)ax.set_ylim(-1.4*0.5*sD, 1.4*0.5*sD)sli_fm.on_changed(update)sli_Rm.on_changed(update)sli_Rd.on_changed(update)sli_n.on_changed(update)sli_rd.on_changed(update)sli_e.on_changed(update)sli_N.on_changed(update)sli_d.on_changed(update)sli_D.on_changed(update)resetax = plt.axes([0.85, 0.01, 0.1, 0.04])button = Button(resetax, 'Reset', color=axcolor, hovercolor='0.975')def reset(event):sli_fm.reset()sli_Rm.reset()sli_n.reset()sli_rd.reset()sli_Rd.reset()sli_e.reset()sli_N.reset()sli_d.reset()sli_D.reset()button.on_clicked(reset)def animate(frame):sfm = sli_fm.valsRm = sli_Rm.valsRd = sli_Rd.valsn = sli_n.valsrd = sli_rd.valse = sli_e.valsN = sli_N.valsd = sli_d.valsD = sli_D.valframe = frame+1phi = 2*np.pi*frame/sfmdraw_pin_init()draw_inner_pin_init()draw_inner_circle_init()pin_update3(sN, se, sd, sD, phi)update_inner_pinA(se, sRm, phi)#update_inner_pinD(se,sRm, phi)# inner_pin_update(sn,sN,srd,sRd,phi)# drive_pin_update(sRm)#update_inner_circle(se,sn,sN,srd,sRd, phi)update_ehypocycloidA(se, sN, sD, sd, phi)update_ehypocycloidD(se, sN, sD, sd, phi)fig.canvas.draw_idle()ani = animation.FuncAnimation(fig, animate, frames=sli_fm.val*(sli_N.val-1), interval=interval)dpi = 100# un-comment the next line, if you want to save the animation as gif:#hypo.animation.save('myhypocycloid.gif', writer='pillow', fps=10, dpi=75)#ani.save('myGUI1.mp4', writer="ffmpeg",dpi=dpi)plt.show()
这里是一段python的算法仿真
算法仿真的结果
结果
intel® RealSense™ D450深度摄像头也是硬件之一,这个东西好像2k
https://www.intel.cn/content/www/cn/zh/products/sku/126367/intel-realsense-vision-processor-d4/downloads.html在这里是我找到了摄像头的相关固件和驱动的下载位置
我也没有这个摄像头只能这样的云体验了

这是现在的价钱

正面

这个是相机的底面,标准的螺纹管以及Type-C的接口

一些硬件参数

以及对应要求的一些驱动主机的基本要求,其实还是主要看接口
USB3.0的速度确实是会快很多
https://www.intelrealsense.com/sdk-2/这里是它的SDK的位置
https://dev.intelrealsense.com/docs这里是它的教程位置,我觉得写的很丰富

攒钱买个硬件就好了,这个这个好哦!

matlab的demo也也有
function depth_example()% Make Pipeline object to manage streamingpipe = realsense.pipeline();% Make Colorizer object to prettify depth outputcolorizer = realsense.colorizer();% Start streaming on an arbitrary camera with default settingsprofile = pipe.start();% Get streaming device's namedev = profile.get_device();name = dev.get_info(realsense.camera_info.name);% Get frames. We discard the first couple to allow% the camera time to settlefor i = 1:5fs = pipe.wait_for_frames();end% Stop streamingpipe.stop();% Select depth framedepth = fs.get_depth_frame();% Colorize depth framecolor = colorizer.colorize(depth);% Get actual data and convert into a format imshow can use% (Color data arrives as [R, G, B, R, G, B, ...] vector)data = color.get_data();img = permute(reshape(data',[3,color.get_width(),color.get_height()]),[3 2 1]);% Display imageimshow(img);title(sprintf("Colorized depth frame from %s", name));end
matlab的读取函数
# Create a context object. This object owns the handles to all connected realsense devicespipeline = rs.pipeline()pipeline.start()try:while True:# Create a pipeline object. This object configures the streaming camera and owns it's handleframes = pipeline.wait_for_frames()depth = frames.get_depth_frame()if not depth: continue# Print a simple text-based representation of the image, by breaking it into 10x20 pixel regions and approximating the coverage of pixels within one metercoverage = [0]*64for y in xrange(480):for x in xrange(640):dist = depth.get_distance(x, y)if 0 < dist and dist < 1:coverage[x/10] += 1if y%20 is 19:line = ""for c in coverage:line += " .:nhBXWW"[c/25]coverage = [0]*64print(line)finally:pipeline.stop()
python的脚本还是看起来比较简单的。
为了让处理的数据更快,可以使用numpy来构造一个数组
import numpy as npdepth = frames.get_depth_frame()depth_data = depth.as_frame().get_data()np_image = np.asanyarray(depth_data)
因为Liberelease帧支持缓冲协议,所以可以使用numpy来这样处理。
机械狗上面都运行着,机器人操作系统ROS(Robotics Operating System)
本次的CyberDog运行的是ROS2

ROS2的构架图
http://doc.tianbot.com/ros2go/http://ros2.bwbot.org/tourial/about-ros2/ros-concepts.html文档地址

这个是要仿照的元祖
波士顿动力的机器人并不过分追求毫厘之间的精确度,追求的是功能的精确性。Atlas 是亚稳态的,因此它在绝大多数时候都是稳定的。处于亚稳态,意味着 Atlas 需要像人类一样保持直立。但即便是 Atlas 所做的后空翻,也只需要 “非常粗略的计算”。当它着陆时,它会对计算做出修正,不需要完美无缺,足够好就行了。其实就是落地的时候有很多的不确定性相当于一个解空间,我们只要选择一个相对比较好的解就好,不需要满足一个定解,在后期进行短暂的修正即可。这样的想法也符合我们人的运动学做法。
众所周知,动物最常见的运动方式是节律运动,即按照。一定的节奏、有力度地重复、协调、持续进行的动作,是低级神经中枢的自激行为。生物学上,动物的节律运动控制区被认为是分层并且模块化的,其控制以中枢模式发生器为中心,既可以接受来自高层的高级神经中枢的主观控制,也可以响应来自躯体各种感受器官的反射,这就是CPG控制机理,也就是所谓的中枢神经发生器。前人已经按照CPG控制机理建立了不同形式的数学模型,它们能够产生的周期振荡的信号,使其能够满足节律运动的特点。

具体的可以去相关论文

我参考的是这篇
基于神经元的模型:Matsuoka神经元震荡模型、Kimura模型等,该类模型生物学意义明确,但参数较多,动态特性分析比较复杂。
基于非线性振荡器的模型:Kuramoto相位振荡器、Hopf谐波振荡器等,该类模型参数较少,模型比较成熟。
https://xw.qq.com/cmsid/20191101A0L4OB00原文在这里

Atlas,跑起来很吊的样子

机械外骨骼
其实这么多年了,并不是只有小米一家发布的机器狗,只不过是小米家的狗摊上了雷军,会营销。也就是所谓的出生好。
| 浙大“绝影”机器狗 |
| 腾讯机器狗Max |
| 宇树科技机器狗 |
| 优必选四足机器人“拓荒牛” |
| 蔚蓝科技阿尔法机器狗 |
最近几年其实出现了这么多的狗,各有其独特的特点,而且普遍都贵。就是卖不出去。而米家的东西一向追求性价比,所以9999是一个很有诚意的价格。

宇树科技是一个2016年成立的年轻公司

也有自己的拳头产品
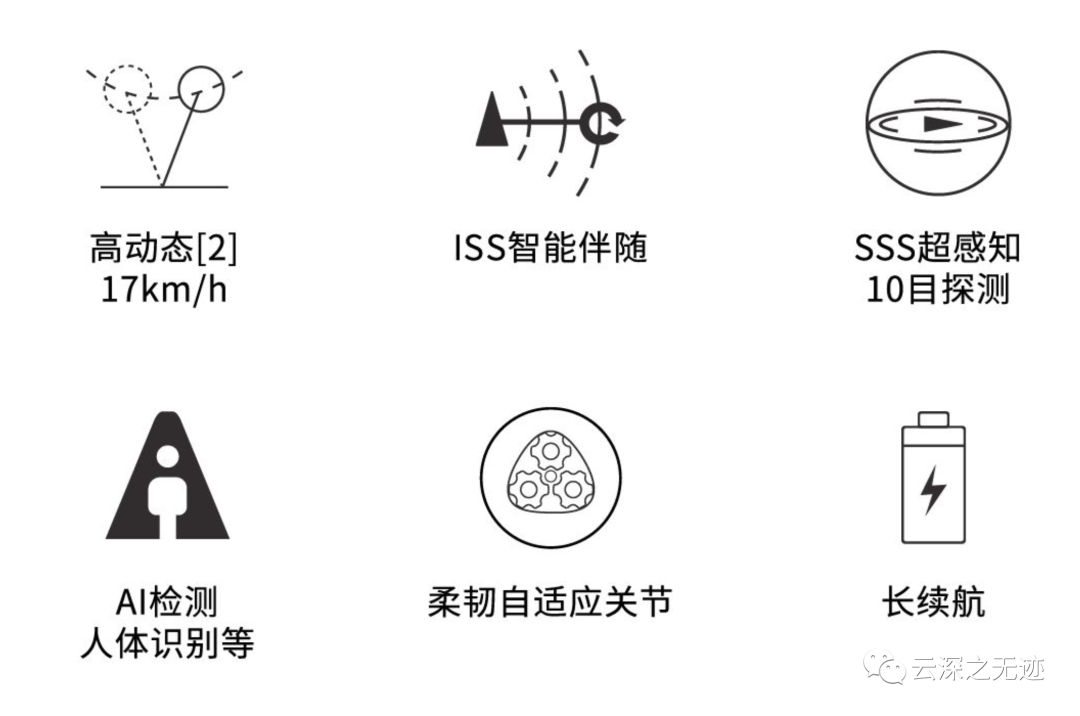
一些特性

负载3~5kg

air版本1.6,均衡1.99,edu5万起。
米家1w的东西又是屠龙刀了
https://www.unitree.com/cn/products/go1
宇树家的东西比较齐全

相关的配置

丰富的接口,为什么没有RJ-45
https://www.unitree.com/cn/products/a1我最喜欢的还是A1


开放的接口,一看就是两套开发板
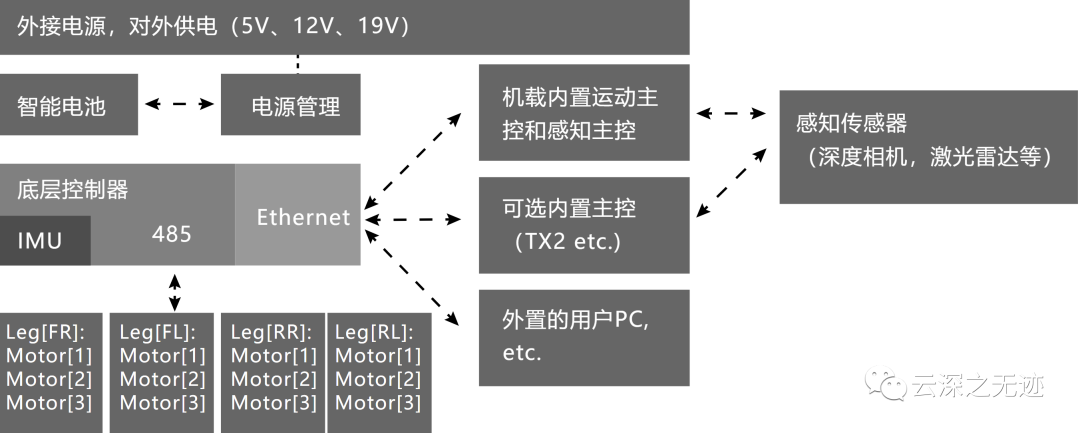
接口框图
https://github.com/unitreerobotics
开源了许多了库,没啥有价值的
又不开源算法
总的来说,小米的东西可能性能不是那么好,算法不是最优。但是它一定是价钱最低,处于一种刚刚好的情况。也不知道就像小米的无人机一样是昙花一现,希望不是。
而且这个1w的价钱真的很便宜,就是我穷而已。也希望小米的逐步开源,我在这边也会持续的跟进。
来自斯坦福的廉价机器狗.上
来自斯坦福的廉价机器狗.中
我以前也写过一些机械狗的东西,只不过后来又更快乐的事情了,就鸽了。
因为每天有很多人在问问题,所以就建立了一个交流群
有需要的可以加进来一起学习