

首先说说电阻(Resistance),在电路中对电流通过具有阻碍作用,并且造成能量消耗的部分,称为电阻。电阻常用R表示,单位欧姆(Ω),导体电阻值由导体的材料、横截面积和长度决定,具体计算不在此赘述。
接下来引出阻抗(Impedance)的概念。在具有电阻、电感和电容的电路里,对电路中的电流所起的阻碍作用叫做阻抗。阻抗常用Z表示,是一个复数,实际称为电阻,虚称为电抗。其中,电容在电路中对交流电所起的阻碍作用称为容抗(Capacitive Reactance) ,电感在电路中对交流电所起的阻碍作用称为感抗(Inductive reactance),电容和电感在电路中对交流电引起的阻碍作用总称为电抗。阻抗的单位是欧姆。
输入阻抗是指一个电路的输入端的等效阻抗。可以理解为在输入端加上电压源U,测量输入端电流I,输入阻抗Rin就等于U/I(将所有电路元件作用的效果总和,等效到一个电阻Rin上)。
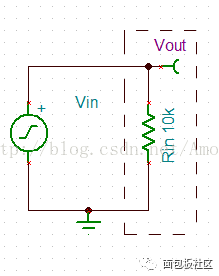
图1.输入阻抗等效电阻示意图
在图1中,Vin为上一级电路的输出信号,作为本级电路的输入信号,Vout为本级电路输出信号的测试点,虚线框内为本级电路的等效输入阻抗,Rin即为电路的输入端等效阻抗。
首先,我们设置输入信号为正弦波,幅值A = 1V,频率f = 10KHz:
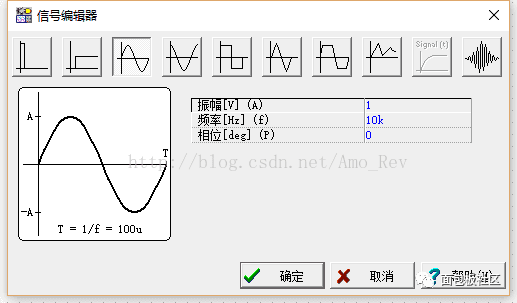
由于信号源内部阻抗为0(上一级电路输出阻抗为0,后面会进行讲解),所以在Vout得到的输出信号应该等于原信号(纯电阻电路,幅值和相位均相等),即Vout = Vin,仿真结果如下:
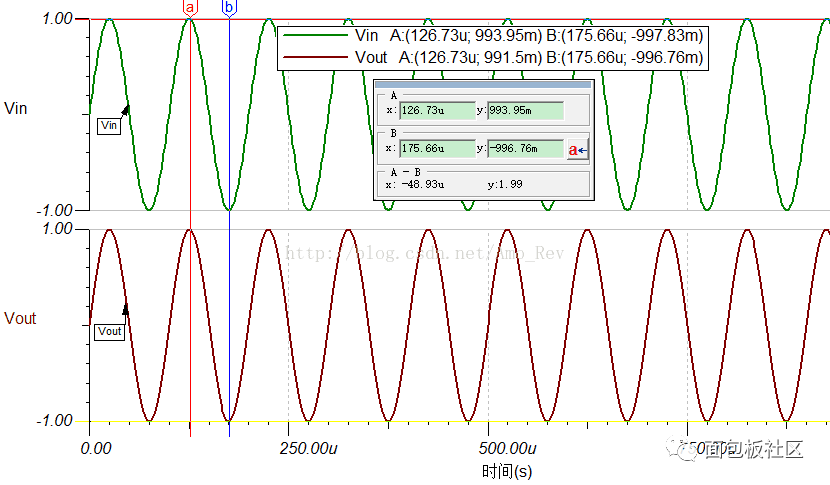
图2.输入端等效阻抗仿真结果
我们通过光标A、B和图例可知,输入信号Vin的幅值A1为993.95mV、-991.83mV,峰峰值Vpp1 ≈1.985mV ≈ 2V;输出信号Vout的幅值A2为991.5mV、997.76mV,峰峰值Vpp2 ≈ 1.989mV ≈ 2V。Vpp1 =Vpp2。
有了输入阻抗的概念之后,我们可以更容易的理解输出阻抗的概念,也就是一个电路输出端的等效阻抗。
让我们先暂时回到高中时代,物理老师告诉我们,电池里面有一个内阻,所以我们可以得到图3这样一个电池模型:
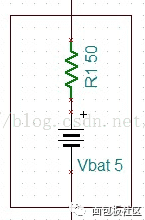
图3.内阻为50Ω的电池模型
我们假设这是一个5V的电池,内部含有50Ω内阻。下面按图4的方式连接电路,将电池加到一个10KΩ的电阻上,然后测一测电阻两端的电压Vout1。
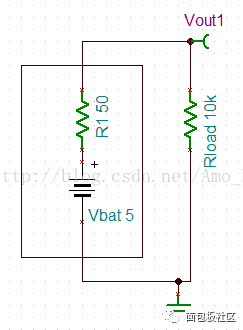
图4.电池模型连接图
我们将仿真结果调出来看看。
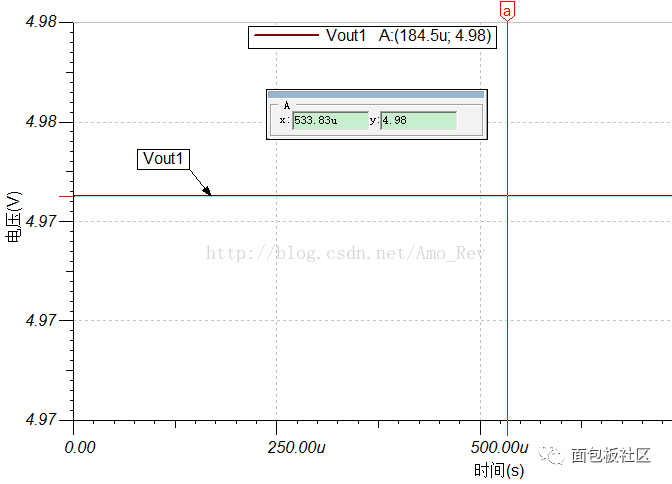
图5.电池模型仿真结果一
从这个结果上看,似乎并不能看出任何东西。那让我们将电池内阻R1分别改为1KΩ、5KΩ、10KΩ、20KΩ,再看一下结果。
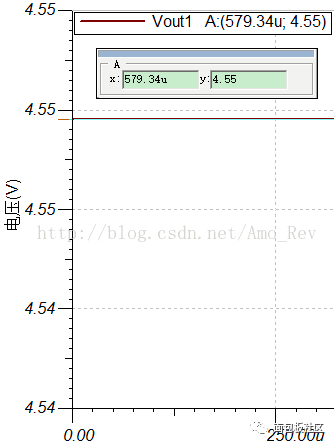
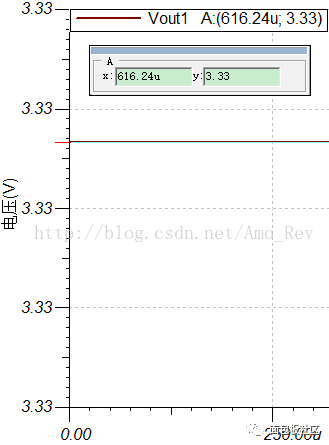
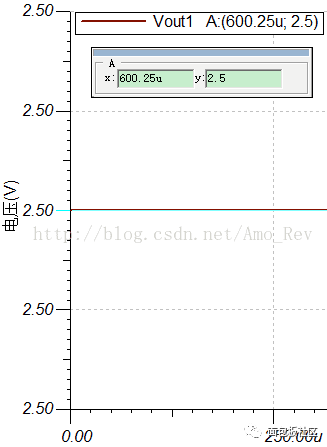

图6.电池内阻为1KΩ(左上)、5KΩ(右上)、10KΩ(左下)、20KΩ(右下)仿真结果二从图例上可以得知,加在电阻Rload两端的直流电压分别为4.55V(1KΩ)、3.33V(5KΩ)、2.5V(10KΩ)、1.67V(20KΩ)。很明显,通过电阻分压公式,我们很容易就得到上面的几个数字:Vout1=5V*Rload/(R1+Rload)。
好了,从高中回到现在。通过刚才的仿真,可以看出,在本级输入阻抗(电池模型里的Rload)不变的情况下,上级电路的输出阻抗(电池内阻R1)越大,本级所能获取的电压信号就越小,正因为如此,在设计需要考虑信号幅值的电路中,我们就需要考虑阻抗匹配的问题。
三、阻抗匹配
阻抗匹配是指信号源或者传输线跟负载之间的一种合适的搭配方式。阻抗匹配分为低频和高频两种情况讨论。
我们先从刚才的电池驱动负载模型(直流电压源驱动负载)入手。我们重新定义负载电阻为R,直流电源电动势为U,内阻为r,我们可以计算出流过负载电阻R的电流I为:
I = U/(R+r)······式1
从式1可以看出,负载R越小,输出电流I越大。
负载R上的电压Uo为:
Uo = IR = U / [ 1+(r/R) ] ······式2
从式2可以看出,负载R越大,则输出电压Uo越高。
有了I和Uo,我们再来计算一下负载R上消耗的功率P:
P = I²×R = [ U/(R+r) ]²×R
= U²×R/( R²+2×R×r+r² )
= U²×R/[ (R-r)²+4×R×r ]
= U²/{ [ (R-r)2/R ] +4×r } ······式3
对于一个给定的信号源,其内阻r是固定的,而负载电阻R是由我们来进行选择的。注意式3中的[ (R-r)2/R ],当R = r,即负载R与信号源内阻r相等时,[ (R-r)2/R ]取得最小值0,此时负载R上可以获得最大输出功率Pmax = U²/(4×r)。即,当负载电阻跟信号源内阻相等时,负载可获得最大输出功率,这就是我们常说的阻抗匹配之一(最大功率传输)。此结论同样适用于低频电路和高频电路。当交流电路中含有容性或感性阻抗时,结论有所改变,就是需要信号源与负载阻抗的的实部相等,虚部互为相反数,这叫做共扼匹配。
在低频电路中,我们一般不考虑传输线阻抗匹配的问题,只考虑信号源与负载的关系,其原因是低频信号波长相对于传输线来说很长,可以将传输线看做“短线”,信号反射问题不用考虑(就像一杯水倒入长江,连一点波澜也掀不起)。举个例子:有一个频率f = 10KHz的信号,根据波长计算公式λ=u/f(λ为波长;u为电磁波在真空中传播速度,近似等于光速3×10e8m)可以计算出该信号波长λ1 = 3×10e8m/10,000Hz = 3,000m。波长3000m远远大于电路中传输线的长度。
在高频电路中,由于信号频率高,波长短,因此还需要考虑反射问题。当波长短得与传输线长度相当时,反射信号与原信号叠加,将会改变原信号形状。如果传输线的特征阻抗与负载阻抗不相等(即不匹配,也称阻抗失配,会形成反射,降低效率;会在传输线上形成驻波,降低传输线有效功率容量降低;严重时会损坏设备,高速信号会产生振荡,辐射干扰等问题)时,在负载端就会产生反射。(传输线特征阻抗,亦称特性阻抗,是由传输线的结构及材料决定的,而与传输线的长度,以及信号的幅度、频率均无关,其他问题可以参考电磁场与电磁波方面关于传输线理论的书籍)
从上述的分析中,我们可以得出以下结论:
(一)需要输出电流大,选择小的负载R;
(二)需要输出电压大,选择大的负载R;
(三)需要输出功率大,选择与信号源内阻匹配的电阻R。
由于很多学习相关电路设计的初学者常用运算放大器进行信号处理,所以给出一些个人建议:
(一)需要保证输入信号幅值不失真,则加大输入电阻;
(二)信号进行运算后如果驱动能力不够(可以理解为输出阻抗过大),后级加单位增益电压缓冲器(电 压跟 随器);
(三)针对具体电路设计要求,选择优先保证信号幅值不失真,还是选择提高带负载能力,从而对输入阻 抗和 输出阻抗进行考虑;
(四)运算放大器输入阻抗和输出阻抗应该参见对应的Datasheet,并不是所有运放的输入阻抗都很大;
(五)信号频率较高时,最好优先选择最大功率传输方式进行阻抗匹配,避免反射,造成运放自激振荡;
(六)如果出现设计之外的信号衰减,请优先考虑阻抗匹配问题。
当电路中出现阻抗不匹配的问题时,我们通常采用以下方法纠正,达到阻抗匹配的目的:
(一)可以考虑用传输线变压器做阻抗匹配(电视机馈线与射频输入端);
(二)可以考虑使用串/并联电容或电感的办法(射频电路调试常用);
(三)可以考虑串/并联电阻的办法(常用)。如果驱动器输出阻抗比较低,可以串联一个大小合适的电阻 (如50Ω、75Ω)与传输线进行匹配;而如果接收器输入阻抗比较高,可以并联一个大小合适的电阻 与传输线进行匹配(“输出端串联匹配,输入端并联匹配”)
来源:面包板社区
—END—
