信号完整性在高频高速电路中十分重要,差分过孔的不连续性会严重影响到信号的完整性,针对高速印制电路板(printed circuit board,PCB)中差分信号与共模信号对差分过孔的低反射、高传输和阻抗稳定的设计要求,首先建立差分过孔的等效物理模型与电路模型进行差分过孔的差分信号与共模信号的性能分析;然后在 PCB 层叠结构和布线模式设计的基础上运用三维电磁仿真软件 HFSS 设置不同的过孔中心距、反焊盘直径及地过孔数量,对差分过孔的时域阻抗、回波损耗、插入损耗进行仿真与分析,并利用 S 参数与时域内阻抗变化,分析过孔的差分性能和共模性能;最后通过仿真结果分析,得出过孔中心距38 mils(1 mil =0. 025 4 mm)、反焊盘直径 32 mils 及使用双过孔地过孔的设置使差分信号和共模信号的性能最优,提出优化了差分过孔的性能的新思路,为高速差分过孔设计提供参考。
引 言
本文通过对差分过孔建立双杆传输线模型,这种简单耦合传输线模型提供了一种分析和预测差分过孔性能的简便途径,确定影响差分过孔性能因素包括过孔中心距、反焊盘直径以及地过孔设置,并在三维电磁仿真软件HFSS 建立物理模型,在模型中分别设置不同的过孔中心距、反焊盘直径以及地过孔数量对过孔性能的影响,通过分析仿真结果中差分信号和共模信号的时域内阻抗变化与 S 参数,对差分过孔的性能进行了优化验证,为高速差分过孔设计提供参考,同时在实际 PCB 生产加工中具有重要的参考价值。
1 差分过孔模型
1. 1 物理模型

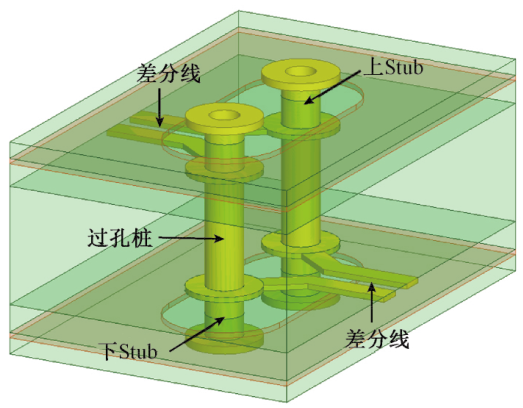
图 1 差分过孔物理模型
1. 2 电路模型
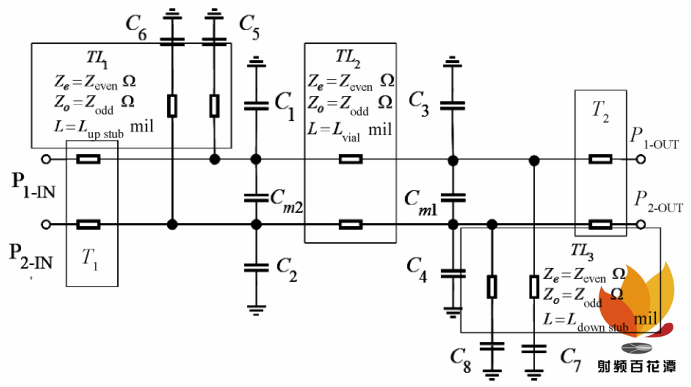
图 2 差分过孔电路模型
如果过孔顶部与底部存在 Stub,Stub 部分将会对信号产生阻抗效应与电容效应,由于差分过孔对的对称性,可知 C 5 = C 6 ,C 7 = C 8 ,当顶部与底部的 Stub 长度与结构一致时,即差分过孔的上下 Stub 部分呈对称性,各个Stub 部分产生的阻抗效应与电容效应是相等的,即 TL 1= TL 2 ,C 5 = C 6 = C 7 = C 8 ,此时,因为过孔内部焊盘的几何形状是相同的,焊盘的有效面积也是一致的,可知 C 1 =C 2 = C 3 = C 4 ,并且内部焊盘之间互感电容也是相等的,即C m1 = C m2 。
对于连接到差分过孔的耦合传输线,当差分过孔两端的信号线的长度一致时,信号线产生的阻抗效应是一致的,而在实际情况中,信号线的长度往往远远大于连接处的长度,因此连接处造成的阻抗不连续性在实际高速通道中可以忽略不计,即 T 1 = T 2 =0。
1. 3 简化模型
差分过孔的俯视图如图 3 所示,在实际情况中,差分过孔的反焊盘为椭圆形,如图3 (a)所示。当模型中的通孔、盲孔或者埋孔满足以下条件:1)PCB 中均匀地填充介电常数为 E r 的介电材料;2)有多个铜层。此时这种差分过孔结构可简化成简单的耦合双杆传输线进行分析 ,两个过孔可视为被连续的导电屏蔽的中心导体,椭圆形的反焊盘结构可被近似为矩形的反焊盘结构,如图 3(b)所示,因此可以运用特征阻抗的闭合形式解决方案去解决这种类型的耦合传输线。
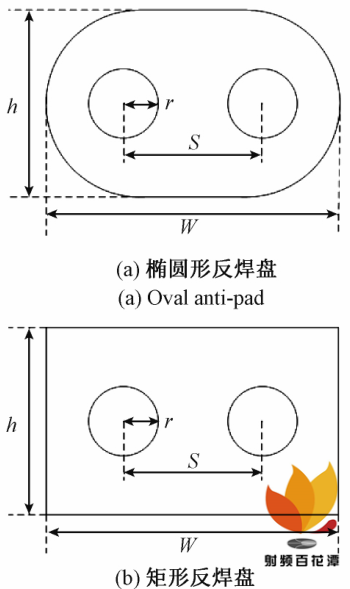
图 3 中具有矩形反焊盘的双杆模型的奇模和偶模阻抗可用式(1)和(2)的闭式方程表示。
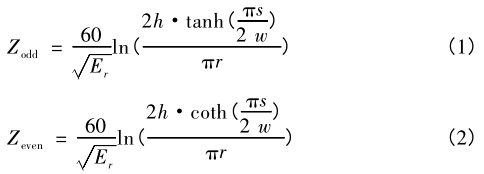
由于反焊盘的宽度 h 即为反焊盘的直径,反焊盘的长度 w 即为反焊盘的直径与过孔的中心距之和,因此式(1)和(2)原始闭式方程可修改为式(3)和(4)。
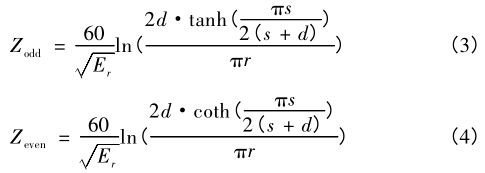
当差分信号加在双杆模型上时,双杆模型处于奇模状态,此时每个单杆的特性阻抗即为单杆的奇模阻抗,差分阻抗是每个单杆模型奇模阻抗的串联,如式(5)所示;当共模信号加在双杆模型上时,双杆模型处于偶模状态,此时每个单杆的特性阻抗即为单杆的偶模阻抗,共模阻抗是每个单杆模型偶模阻抗的并联,如式(6)所示。
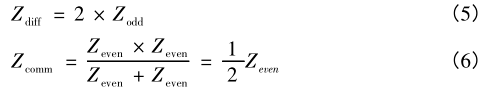
式中:Z odd 为奇模阻抗;Z even 为偶模阻抗;Z diff 为差分阻抗;Z comm 为共模阻抗;E r 为材料的介电常数;s 为过孔中心距;r 为过孔半径;w 为反焊盘长度;h 为反焊盘宽度;d 为反焊盘直径。
2 仿真验证
2. 1 建立模型
差分线分布于 PCB 顶层与底层,根据 PCB 具体层叠结构与 100 Ω 的差分阻抗值,其中 100 Ω 为差分阻抗的参考值,可以利用 Si9000 计算参考阻抗要求下的走线宽度和线间距。经过计算线宽、线距均设置为 6 mil。差分线通过差分过孔连接在一起,差分过孔的内部直径为10 mil,外部直径为 20 mil,孔长为 60. 2 mil,差分过孔参数为常用设置,也是生产工厂的生产工艺能力范围之内,生产的成本最低。板材为常用板材 FR -4,其介电常数为 4. 4,反焊盘形状为椭圆形,s 为过孔中心距,d 为反焊盘直径,模型如图 4 所示。通过以上的分析,两个过孔的中心距 s 以及反焊盘的直径 d 是影响差分过孔性能的重要因素。同时在高速设计中,接地过孔可以放置在信号过孔附近,以提供电流返回路径,此举有助于降低由于接地电流返回路径引起的寄生接地电感,可以改善信号的回波损耗和插入损耗,因此在模型中分别改变过孔中心距,反焊盘直径及差分过孔旁地过孔数量,经过 HFSS 仿真之后分析各因素对差分信号与共模信号的影响,并优化差分过孔的设计。
2. 2 过孔中心距对过孔性能影响
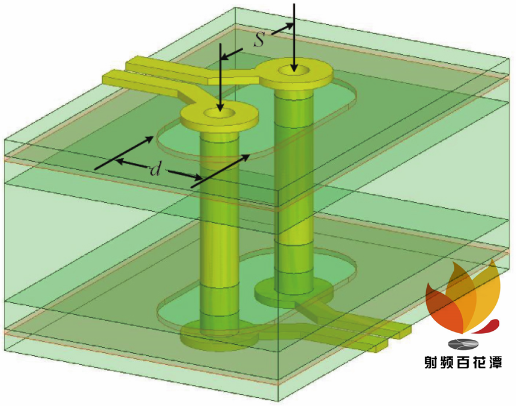
图 4 本文差分过孔模型
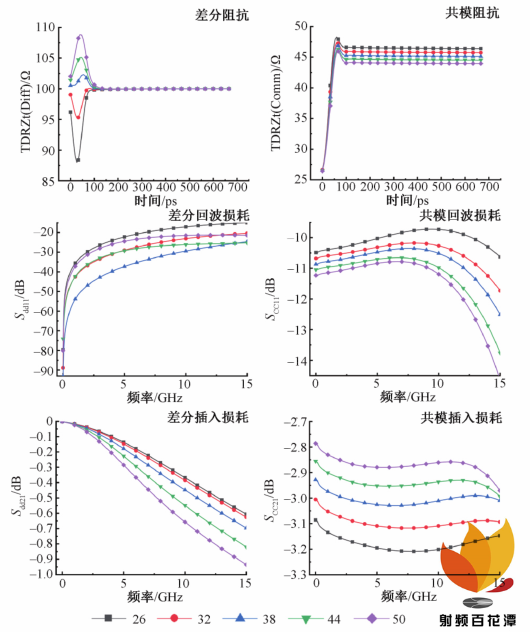
综合以上分析,过孔中心距的变化对差分信号与共模信号的信号完整性影响是不同的,当过孔的中心距逐渐增大时,过孔间的耦合减弱,每个过孔的奇模阻抗将会增大,偶模阻抗将会减小,这意味着差分阻抗将会增大,共模阻抗将会减小。总体来说,对于差分信号,过孔中心距过大或过小均会对其信号完整性产生不利影响;而对于共模信号,过孔中心距增大则会对信号完整性有一定的提升。
2. 3 反焊盘直径对过孔性能影响
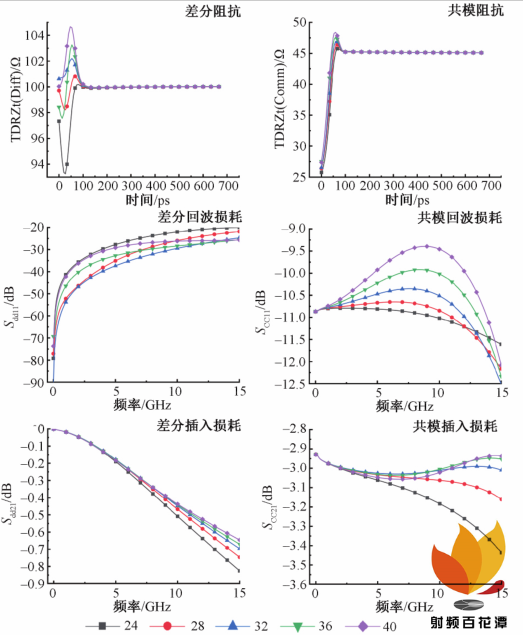
从图 6 与表 2 可知,对于差分信号,当反焊盘直径逐渐增大时,差分阻抗变化的区间相对于过孔 100 Ω 的差分参考阻抗值,变化幅度最大百分比分别为 6. 9%、2. 6%、-2. 2%、-5. 7%、-4. 7%,可见反焊盘直径为 32mil 时,差分过孔阻抗的变化幅度最小,此时差分过孔阻抗的连续性和稳定性最好,差分信号的反射系数 S dd11 也是最小,其回波损耗将至最低;而差分信号的传输系数S dd21 则随着反焊盘直径的增大而小幅度增大,其插入损耗则有一定程度的减小。对于共模信号,当反焊盘直径逐渐增大时,共模阻抗的变化范围会有小幅度的增大,最后都稳定在 45. 2 Ω 的稳定值;同时共模信号的反射系数S cc11 也依次小幅度的增大,但其变化范围小于 1. 5 dB,回波损耗也依次小幅度增大;其传输系数 S dd21 在反焊盘直径增大的情况下会有一定程度的增大,但其变化范围也仅仅为 0. 5 dB,插入损耗也依次小幅度减小。
综合以上分析,反焊盘直径的变化对差分信号与共模信号的信号完整性影响是不同的,总体来说,对于差分信号,反焊盘直径过大或过小均会对其信号完整性产生不利影响;对于共模信号来说,反焊盘直径的变化对共模信号的信号完整性的影响是比较小的,其影响在可接受的范围之内。
2. 4 地过孔对过孔性能影响
为验证地过孔对差分过孔性能的影响,建立图4 模型,分别在差分过孔旁设置无地过孔,单地过孔以及双地过孔的情况,其中地过孔孔径为 24 mil,距离较近差分过孔的间距为 31 mil,差分过孔的中心距设置为38 mil,反焊盘的直径设置为 32 mil,差分过孔旁设置单地过孔与双地过孔的模型如图 7 所示。图 8 所示为这3 种不同的物理模型的差分信号与共模信号的阻抗、回波损耗以及插入损耗的比较。从图 8 可知,对于差分信号,在无地过孔,单地过孔以及双地过孔的 3 种情况下,差分阻抗变化幅度与反射系数 S dd11 基本上在小范围内浮动;而差分信号的传输系数 S dd21 则在这 3 种情况下依次增大,插入损耗会依次减小。对于共模信号,在无地过孔,单地过孔以及双地过孔的 3 种情况下,共模阻抗的变化范围越来越小,尤其在增加了双地过孔后,共模阻抗能够快速稳定在 25 Ω 的参考值;同时共模信号的反射系数 S cc11 均有一定程度的减小,回波损耗依次减小;其传输系数 S cc21 则依次明显增大,插入损耗依次减小。
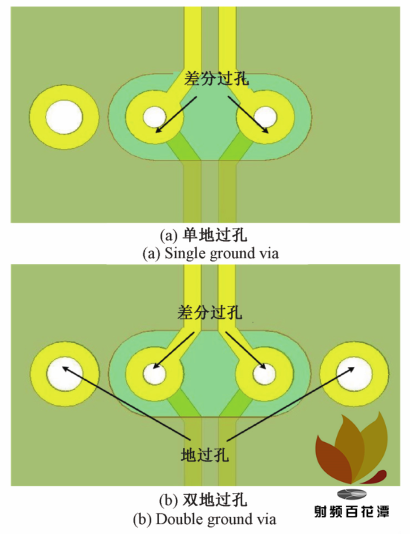
图 7 单地过孔与双地过孔的模型
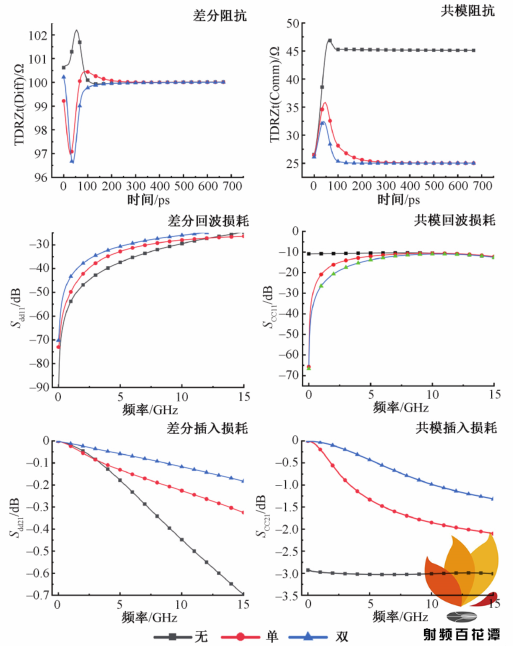
图 8 不同地过孔数量仿真结果曲线
3 结 论
本文通过建立差分过孔的等效物理与电路模型进行差分过孔的差分信号与共模信号的性能分析,并在 PCB层叠结构和布线模式设计的基础上,利用 HFSS 设置不同的过孔中心距、反焊盘直径及地过孔数量,对差分过孔的时域阻抗、回波损耗、插入损耗进行仿真与分析,可得到如下结论。
1)过孔中心距的变化对差分信号与共模信号的信号完整性影响是不同的。总体来说,对于差分信号,过孔中心距过大或过小均会对信号完整性产生不利影响。对于共模信号,过孔中心距增大对信号完整性有一定的提升。
2)反焊盘直径变化对差分信号与共模信号的信号完整性影响是不同的。总体来说,对于差分信号,反焊盘直径过大或过小均会对其信号完整性产生不利影响;对于共模信号,反焊盘直径的变化对共模信号的信号完整性的影响是比较小的,其影响在可接受的范围之内。
3)地过孔数量对差分信号与共模信号的信号完整性影响也是不同的。总体来说,无地过孔,单地过孔以及双地过孔均会依次提高差分信号与共模信号的信号完整性,尤其对共模信号的信号完整性的提升更为显著。
以上结论为差分过孔设计及其高频特性影响分析提供了一定依据,对于高速 PCB 中差分过孔设计具有一定的指导意义。

声明:
投稿/招聘/推广/宣传 请加微信:15989459034
