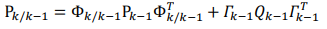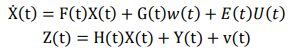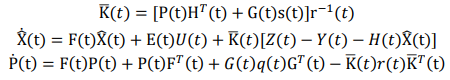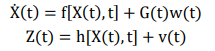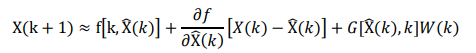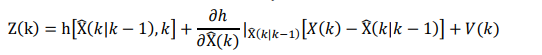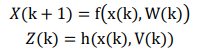2021年6月17日9时22分,搭载神舟十二号载人飞船的运载火箭,在酒泉卫星发射中心点火发射。此后,神舟十二号载人飞船与火箭成功分离,进入预定轨道,顺利将聂海胜、刘伯明、汤洪波3名航天员送入太空,发射取得圆满成功。在载人飞船运行的过程中,需要严格观测及控制其运行轨迹。谈到载人航天,不得不提及人类历史上第一次登月,阿波罗登月,阿波罗号成功的背后是运用了卡尔曼滤波。那什么是滤波?滤波是指从含有干扰的接收信号中提取有用信号的一种技术,是一种增强有用信号的数字信号处理过程。在数据通信中,无用信号表现为特定波段频率和杂波,通常是一个随机过程。卡尔曼滤波是最优滤波中的一种常用算法,是以实现信号或状态的最优估值与相应的真实值的误差的方差最小。最早实现卡尔曼滤波器的是斯坦利·施密特。鲁道夫·卡尔曼在访问NASA埃姆斯研究中心时,将斯密特的方法应用于阿波罗计划的轨道预测,并于1960年,提出离散系统卡尔曼滤波,后又将该种方法推广到连续时间系统中。正是由于卡尔曼滤波从时域分析处理数据,不仅可以处理平稳随机过程,也可以处理非平稳随机过程,所以被广泛应用于各种领域,例如惯性导航,定位系统,经济投资等。图:惯性导航(图源:https://m.sohu.com/a/192009289_819742/)
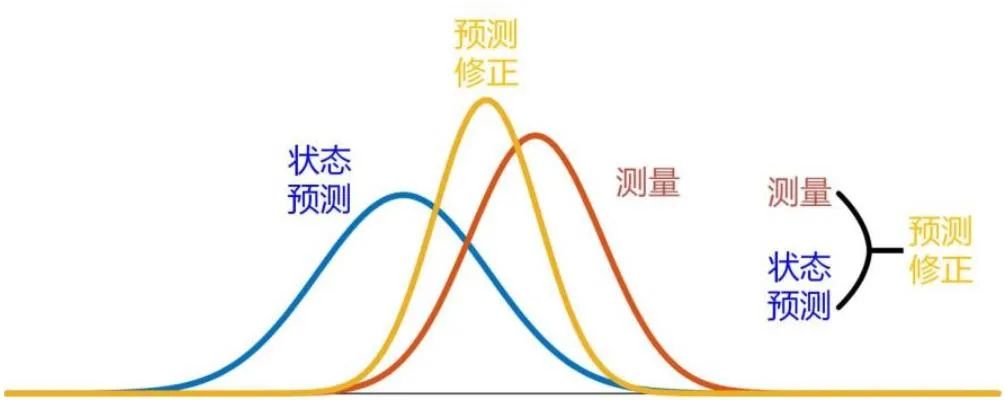
图:卡尔曼滤波过程(图源:https://zhuanlan.zhihu.com/p/223091952)
常见的卡尔曼滤波主要分为离散型卡尔曼滤波和连续型卡尔曼滤波。递推算法的使用是卡尔曼滤波的一大优点,因此离散型卡尔曼滤波在工程上得到了广泛的运用。在一个滤波周期内,根据卡尔曼滤波对使用系统信息和量测信息的先后次序,可以将卡尔曼滤波划分为时间更新过程和量测更新过程,主要分为以下几个部分。1.一步预测:根据k-1时刻的状态估计预测k时刻的状态,通过k-1个时刻的量测量对k时刻状态量进行线性最小方差估计。2.状态估计方程:通过利用残差(新息),对状态量进行修正估计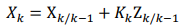
其中,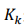 是对残差的加权阵,被称为滤波增益阵。3.滤波增益阵和估计均方误差阵的推导:最佳滤波增益阵使得估计的均方误差达到最小。
是对残差的加权阵,被称为滤波增益阵。3.滤波增益阵和估计均方误差阵的推导:最佳滤波增益阵使得估计的均方误差达到最小。
其中,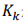 是最佳增益阵,
是最佳增益阵,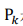 是最小均方误差阵。
是最小均方误差阵。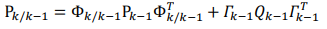
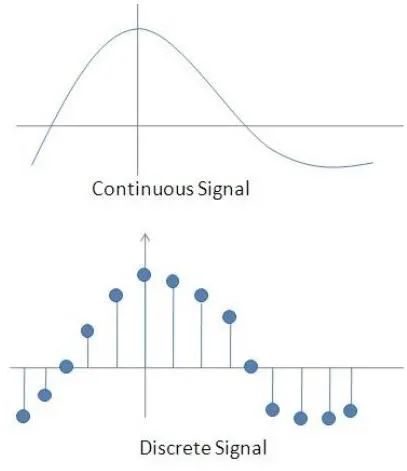
(1)递推算法的使用,使得数据的存储量减少,通过滤波步数的增加,提取出的信息量在增大。(2)只须知道驱动噪声的统计特性,使得卡尔曼滤波能对非平稳的被估计量做估计。图:连续信号离散化(图源:https://www.cnblogs.com/noah0532/p/8684845.html)连续型卡尔曼滤波可以在离散型卡尔曼滤波的基础上进行推导,通过将连续系统离散化,应用离散型卡尔曼滤波基本方程和导数运算推导出连续型滤波方程。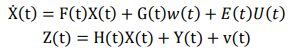
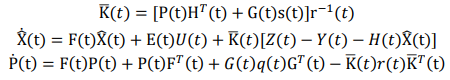
图:制导系统(图源:https://www.kepuchina.cn/mil/news/202007/t20200724_1655083.shtml)上述卡尔曼滤波问题都是假设物理系统的数学模型是线性的,但是线性模型只是理想化,实际工程中很多的模型都是非线性的。同时,在非线性系统中,如果系统噪声和观测噪声都是任意分布,那么系统的处理难度会更大。因此,一般会对噪声的统计特性给出符合实际而又便于数学处理的设定。非线性系统的数学模型如下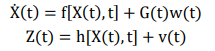
其中,w(t)和v(t)是彼此不相关的零均值白噪声序列,它们与初始状态X(0)也不相关。针对扩展卡尔滤波,利用非线性函数的局部线性特性,将非线性模型局部线性化,通常是将非线性函数f围绕滤波值做一阶Taylor展开。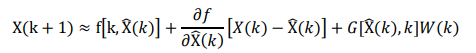
此外,将非线性函数h围绕滤波值做一阶Taylor展开。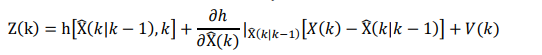
线性化后,对其运用线性卡尔曼滤波基本方程,便可获得扩展卡尔曼滤波递推方程。扩展卡尔曼滤波是对非线性的系统方程或者观测方程进行泰勒展开并保留一阶近似项,引入了线性化误差。无迹卡尔曼滤波摒弃了对非线性函数进行线性化的传统做法,采用卡尔曼线性滤波框架,对于一步预测方程,使用无迹变换来处理均值和协方差的非线性传递问题。什么是无迹变换呢?在原状态分布中按照某一规则选取一些采样点,他们的均值和协方差等于原状态分布的均值和协方差;并将他们带入非线性函数,获取相应函数值的点集。对这些点求取变换后的均值和协方差。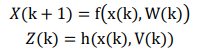
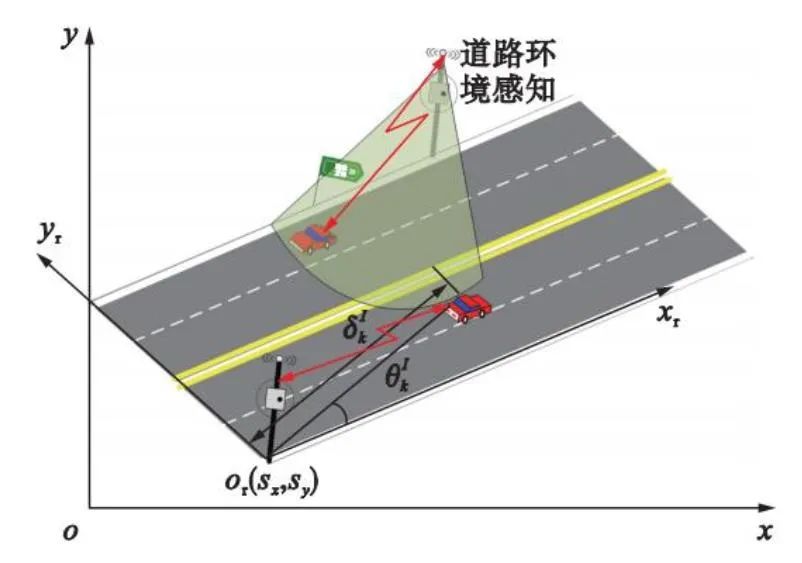
根据上述无迹变换,对非线性系统进行变换处理。不同于在估计点处做Taylor级数展开,再进行n阶近似,而是在估计点附件进行无迹变换,使得Sigma点集的均值和协方差与原统计特性匹配,再对这些Sigma点集进行非线性映射,获得状态概率密度函数,实现一种统计近似。图:路测传感器测量模型(图源:崔雅博,王晓婷.基于IMM-UKF 的协同式车辆运动状态跟踪算法)针对前面几种卡尔曼滤波,不必知道目标的运动模型就能够实时修正目标的状态参量,具有较好的适应性,但是如果目标实施突然的运动变化时,基本的卡尔曼滤波就无法获取好的结果了。交互式多模型卡尔曼滤波是一种软切换算法,使用两个或者更多的模型描述工作过程中的状态,利于减小单模型估计误差较大的影响。交互式多模型卡尔曼滤波的思想是在每一个时刻,假设某个模型在当下时刻有效,然后混合前一时刻所有滤波器的状态估计值,获取与这个特定模型匹配的滤波器的初始条件,然后对每个模型并行实施滤波,然后,以模型匹配似然函数为基础更新模型概率,并组合所有滤波器修正后的状态估计值以得到状态估计。在使用该算法时,对于滤波器的目标运动模型的选择,需要从以下几个方面进行考虑。1.滤波器个数的选择,包括较为精确的模型和较为粗糙的模型。2.马尔科夫链状态转移概率的选取对滤波器的性能有较大影响,会直接影响模型误差和模型概率估计的准确性。3.该算法具有模块化的特性,当使用的时候,无法预料目标的运动规律时,应该选择一般的鲁棒性较强的模型。参考文献:
1.严恭敏,《捷联惯导算法与组合导航原理》
2.黄小平,王岩,《卡尔曼滤波原理及应用》
3.秦永元,张洪钺,汪叔华《卡尔曼滤波与组合导航原理》
4.赵树杰,《信号检测与估计理论》
5.崔雅博,王晓婷.基于IMM-UKF的协同式车辆运动状态跟踪算法.沈阳工业大学学报
作者:凌霄
浙江大学机械电子专业博士,从事智能传感与人机交互,智能机器人控制等领域的研究
免责声明:本文版权归原作者所有。本文所用视频、图片、文字如涉及作品版权问题,请第一时间告知,我们将根据您提供的证明材料确认版权并按国家标准支付稿酬或立即删除内容!本文内容为原作者观点,并不代表本公众号赞同其观点和对其真实性负责。



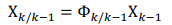
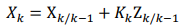
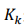 是对残差的加权阵,被称为滤波增益阵。
是对残差的加权阵,被称为滤波增益阵。
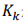 是最佳增益阵,
是最佳增益阵,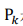 是最小均方误差阵。
是最小均方误差阵。