
来源 | FPGA之家
智库 | 云脑智库(CloudBrain-TT)
一、傅立叶变换的由来
四、傅立叶变换的物理意义
傅立叶变换是数字信号处理领域一种很重要的算法。要知道傅立叶变换算法的意义,首先要了解傅立叶原理的意义。傅立叶原理表明:任何连续测量的时序或信号,都可以表示为不同频率的正弦波信号的无限叠加。而根据该原理创立的傅立叶变换算法利用直接测量到的原始信号,以累加方式来计算该信号中不同正弦波信号的频率、振幅和相位。
和傅立叶变换算法对应的是反傅立叶变换算法。该反变换从本质上说也是一种累加处理,这样就可以将单独改变的正弦波信号转换成一个信号。因此,可以说,傅立叶变换将原来难以处理的时域信号转换成了易于分析的频域信号(信号的频谱),可以利用一些工具对这些频域信号进行处理、加工。最后还可以利用傅立叶反变换将这些频域信号转换成时域信号。
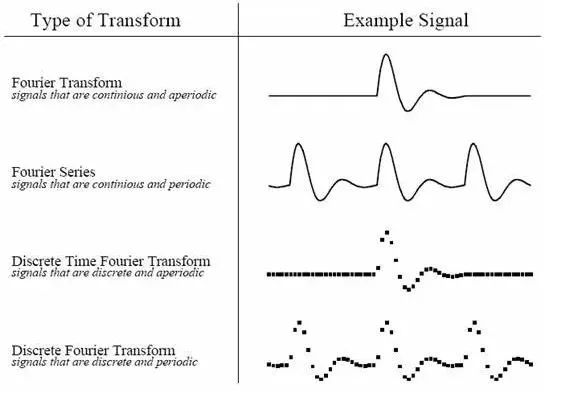
从现代数学的眼光来看,傅里叶变换是一种特殊的积分变换。它能将满足一定条件的某个函数表示成正弦基函数的线性组合或者积分。在不同的研究领域,傅里叶变换具有多种不同的变体形式,如连续傅里叶变换和离散傅里叶变换。
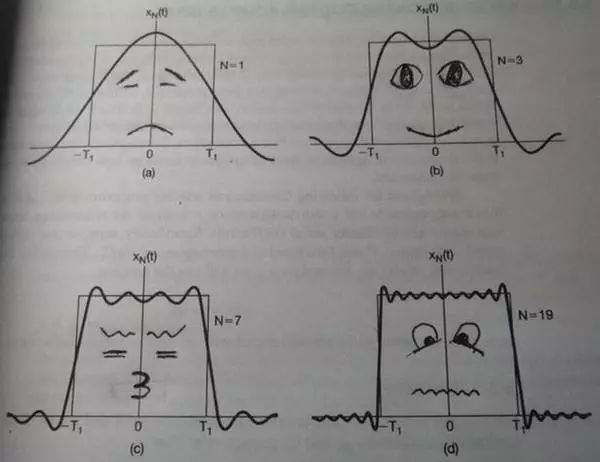
在数学领域,尽管最初傅立叶分析是作为热过程的解析分析的工具,但是其思想方法仍然具有典型的还原论和分析主义的特征。"任意"的函数通过一定的分解,都能够表示为正弦函数的线性组合的形式,而正弦函数在物理上是被充分研究而相对简单的函数类:
傅立叶变换是线性算子,若赋予适当的范数,它还是酉算子;
傅立叶变换的逆变换容易求出,而且形式与正变换非常类似;
正弦基函数是微分运算的本征函数,从而使得线性微分方程的求解可以转化为常系数的代数方程的求解。在线性时不变的卷积运算为简单的乘积运算,从而提供了计算卷积的一种简单手段;
离散形式的傅立叶的物理系统内,频率是个不变的性质,从而系统对于复杂激励的响应可以通过组合其对不同频率正弦信号的响应来获取;
著名的卷积定理指出:傅立叶变换可以化复变换可以利用数字计算机快速的算出(其算法称为快速傅立叶变换算法 (FFT))。
正是由于上述的良好性质,傅里叶变换在物理学、数论、组合数学、信号处理、概率、统计、密码学、声学、光学等领域都有着广泛的应用。
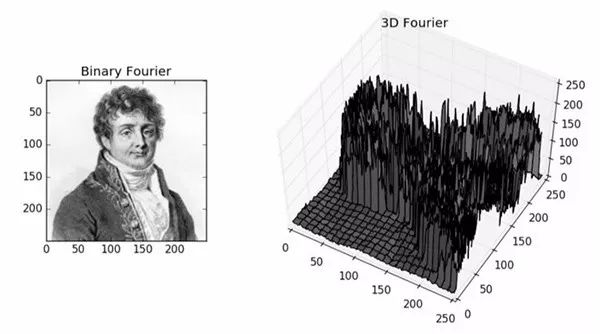
五、图像傅立叶变换的物理意义
图像的频率是表征图像中灰度变化剧烈程度的指标,是灰度在平面空间上的梯度。如:大面积的沙漠在图像中是一片灰度变化缓慢的区域,对应的频率值很低;而对于地表属性变换剧烈的边缘区域在图像中是一片灰度变化剧烈的区域,对应的频率值较高。傅立叶变换在实际中有非常明显的物理意义,设f是一个能量有限的模拟信号,则其傅立叶变换就表示f的谱。
从纯粹的数学意义上看,傅立叶变换是将一个函数转换为一系列周期函数来处理的。从物理效果看,傅立叶变换是将图像从空间域转换到频率域,其逆变换是将图像从频率域转换到空间域。换句话说,傅立叶变换的物理意义是将图像的灰度分布函数变换为图像的频率分布函数,傅立叶逆变换是将图像的频率分布函数变换为灰度分布函数。
傅立叶变换以前,图像(未压缩的位图)是由对在连续空间(现实空间)上的采样得到一系列点的集合,我们习惯用一个二维矩阵表示空间上各点,则图像可由z=f(x,y)来表示。由于空间是三维的,图像是二维的,因此空间中物体在另一个维度上的关系就由梯度来表示,这样我们可以通过观察图像得知物体在三维空间中的对应关系。
为什么要提梯度?因为实际上对图像进行二维傅立叶变换得到频谱图,就是图像梯度的分布图,当然频谱图上的各点与图像上各点并不存在一一对应的关系,即使在不移频的情况下也是没有。傅立叶频谱图上我们看到的明暗不一的亮点,实际上图像上某一点与邻域点差异的强弱,即梯度的大小,也即该点的频率的大小(可以这么理解,图像中的低频部分指低梯度的点,高频部分相反)。
一般来讲,梯度大则该点的亮度强,否则该点亮度弱。这样通过观察傅立叶变换后的频谱图,也叫功率图,我们首先就可以看出,图像的能量分布,如果频谱图中暗的点数更多,那么实际图像是比较柔和的(因为各点与邻域差异都不大,梯度相对较小),反之,如果频谱图中亮的点数多,那么实际图像一定是尖锐的,边界分明且边界两边像素差异较大的。
对频谱移频到原点以后,可以看出图像的频率分布是以原点为圆心,对称分布的。将频谱移频到圆心除了可以清晰地看出图像频率分布以外,还有一个好处,它可以分离出有周期性规律的干扰信号,比如正弦干扰,一副带有正弦干扰,移频到原点的频谱图上可以看出除了中心以外还存在以某一点为中心,对称分布的亮点集合,这个集合就是干扰噪音产生的,这时可以很直观的通过在该位置放置带阻滤波器消除干扰。
另外我还想说明以下几点:
图像经过二维傅立叶变换后,其变换系数矩阵表明:若变换矩阵Fn原点设在中心,其频谱能量集中分布在变换系数短阵的中心附近。若所用的二维傅立叶变换矩阵Fn 的原点设在左上角,那么图像信号能量将集中在系数矩阵的四个角上。这是由二维傅立叶变换本身性质决定的。同时也表明一股图像能量集中低频区域。
变换之后的图像在原点平移之前四角是低频,最亮,平移之后中间部分是低频,最亮,亮度大说明低频的能量大(幅角比较大)。
— The End —
声明:本公众号目前所载内容为本公众号原创、网络转载或根据非密公开性信息资料编辑整理,相关内容仅供参考及学习交流使用。由于部分文字、图片等来源于互联网,无法核实真实出处,如涉及相关争议,请跟我们联系。我们致力于保护作者知识产权或作品版权,本公众号所载内容的知识产权或作品版权归原作者所有。本公众号拥有对此声明的最终解释权。
投稿/招聘/推广/合作/赞助 请加微信:15881101905(手机同号)

@智说 “ 阅读是一种习惯,分享是一种美德,我们是一群有态度的知识传播者!”
↓↓↓ 戳#阅读原文# ,加入#知识星球#,精彩继续 ^_^