1DOE的设计思想
衍射光学元件(DiffractiveOptical Elements，简称DOE)的设计理论通常分为两类：标量衍射理论和矢量衍射理论。当衍射光学元件的横向特征尺寸大于入射光波长时，用标量衍射理论设计衍射光学元件具有极大的优势。
标量衍射模型认为DOE是无限薄的曲面，是一种纯相位调制元件。纯相位型调制元件的优势在于不会引起光能被吸收而损失掉，因此，理论上用纯相位型调制元件可以获得更高的衍射效率。
相位衍射元件的透过率函数可以表式为：
式中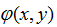
为DOE的位相分布函数。设入射到DOE的光场复振幅分布为
，则从DOE出射的光场复振幅分布为
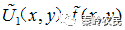，根据标量衍射公式，即可求出DOE后任一点的光场。
根据标量衍射理论，傍轴条件下，衍射光学系统可看成是一种从输入波前到输出波前的变换问题。无论DOE实现何种特殊的功能(光束整形、分束、合束等)，无论是在菲涅尔衍射还是在夫琅禾费衍射区，衍射光学系统均可认为是一种空间线性变换系统。入射场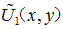
与输出场(接收场)
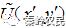之间有如下关系：
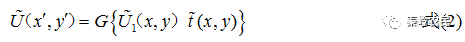
对于不同的功能和光学系统，G代表不同的变换。
因此，DOE的设计思想可表述为，利用具有位相分布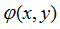
的DOE调制入射场
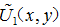，使其经变换G后得到所需要的输出场分布
。
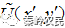多数情况下，上述问题无法进行解析求解，需将其转化为数值优化问题，利用优化算法寻求在某种范数下的最优解。
因此，DOE求解问题的实质归结为：求DOE上的相位分布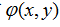
，使得最
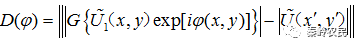
小。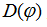
为某种范数下实际值与理想值间的差异。
标量衍射理论起步早，发展成熟，目前已级产生了GS算法及其改进算法、杨顾(YG)算法及其改进算法、模拟退火算法(SA)、遗传算法(GA)等优化算法及各种混合算法，各种优化算法之间的关系如图1所示。
GS算法是1971年由R.W.Gerchberg和W.O.Saxton提出的一种具有实际意义振幅位相恢复算法。利用输入光场与输出光场间的正逆傅里叶变换以及输入输出面上的光场限制条件，通过反复迭代，直到满足设计要求。 GS算法的具体内容详见第3.3节。为提高GS算法的收敛速度，并克服GS算法易于陷于局部极值点的缺陷，获得更理想的光斑输出，又陆续发展了多种GS算法的改进算法，如位相混合算法、输入-输出算法等，均为调整输入面的限制条件或焦平面的限制条件，来改善位相分布或设计性能，但本质都是一样的。
更普遍的迭代算法是YG算法(杨-顾算法)，该算法是中科院物理所的杨国桢和顾本源于20世纪80年代初基于应用光学一般变换理论提出的幺正变换系统中振幅-位相恢复问题的一般描述。在严格数学推导的基础上，建立一组确定振幅-位相分布的联立方程组，并将其推广到非幺正变换系统中。YG算法原则上可解决任意线性变换系统中的振幅-相位恢复问题，而GS算法是YG算法的一个特例。利用YG算法进行二元光学器件的位相设计也有很多成功的案例。
GS、YG算法均是一种局部优化算法，而模拟退火(SA:Stimulated Annealing)算法借鉴不可逆动力学思想，是一种基于蒙特卡洛迭代求解的启发式随机优化算法，理论上是一种全局优化算法，它不同于局部优化算法之处在于：以一定概率选择邻域中评价函数值大的状态。SA算法的基本思想是：将优化变量的可能取值Si看成某一物质体系的微观状态，而将评价函数C(Si)看成该物质体系在对应状态下的内能，并用控制参量T类比温度。在某一温度下，经不断降温，在全局解空间中随机搜索最优解，同时具有概率突跳特点，即在局部极小以一定概率跳出并最终趋于全局最优。
遗传算法(GA：GeneticAlgorithm)借鉴生物进化论的思想，是一种启发式群体概率性迭代优化方法。GA将问题的求解表示成“染色体”的适者生存过程，其中包括选择、交叉和变异操作，通过“染色体”群的一代代不断进化，最终收敛到“最适应环境”的个体，从而求得问题的最优解。GA算法具有并行搜索能力，同时不依赖问题的特殊信息，但存在进化缓慢和“早熟”现象。
共轭梯度算法是目前解决非线性无约束最优化问题的常用方法之一。把输出平面上的相位分布视为自由变量，引入一个误差函数E来评价所设计的衍射相位元件的性能，从而把衍射相位元件的设计问题归结为去寻求一组相位分布使误差函数E达到极小值的问题。由于该方法不涉及二阶偏微分矩阵，故计算所用的计算内存较小。
混合优化算法是一种能将全局优化算法与局部优化算法有机结合起来的算法，既有一定的全局搜索能力，又具有较高的优化效率，才可保证在较短时间内获得优良性能的位相分布，是目前DOE设计中使用较多的算法。例如，GLUSA联合运用了遗传、模拟退炎有爬山法各自的优点，依次经过参量初始化、基因交换、全局搜索及调整参量并不断重复等过程，最终达到获得最优解的目的。全局算法、局部算法和混合算法的优缺点具体见表1。
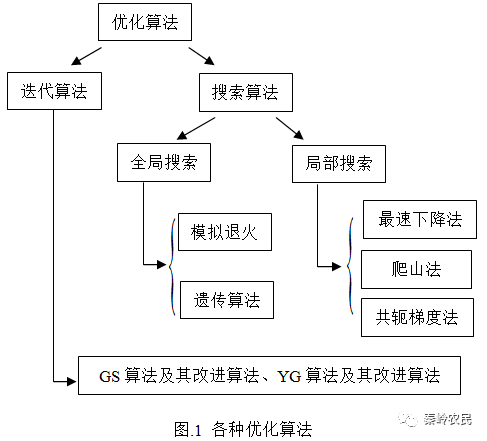
图2是衍射系统的光路简图，系统的光轴与所选坐标系的z轴一致，DOE(输入面)和接收屏(输出面)分别放在P1和P2位置，间距为L。
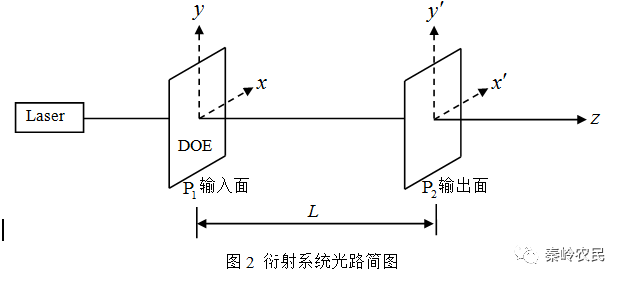
设输入光波场的振幅为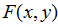
，DOE的相位分布为
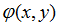，输出面上预期的光场振幅为
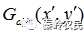，输入光场由DOE调制后经傅里叶变换在输出面上的实际光场振幅分布为
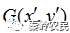，相位为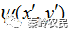
。
根据标量衍射理论，在远场条件下(距离L增大到一定条件)，利用夫琅禾费衍射积分公式有：
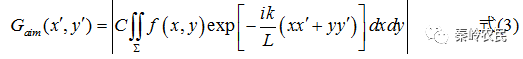
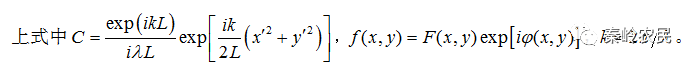
实际设计DOE的过程中，对上式的求解也是非常重要的。
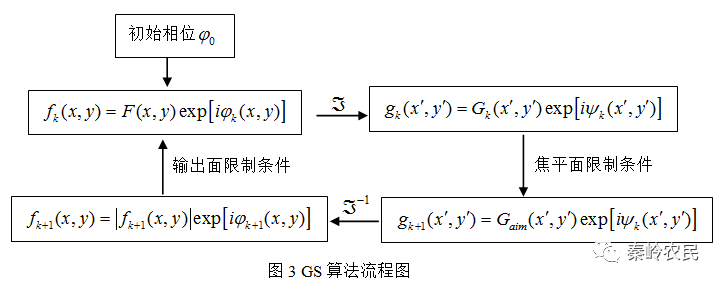
图3.2是GS算法设计思想的流程，具体实现步骤可做如下描述：
(1)取任意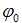
作为入射面的初始相位分布，与入射光振幅
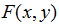相结合，得到入射光射面的复振幅
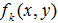，此时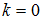
。
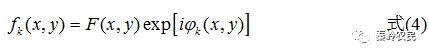
(2)从输入面到输出面做傅里叶变换得到复振幅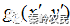
，FFT表示傅里叶变换。
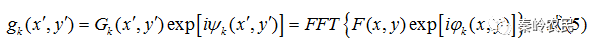
(3)取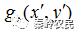
的相位函数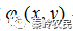
与衍射面预期得到的目标振幅函数
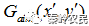相结合，得到新的光的光场分布函数
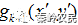，此时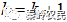
。
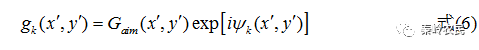
(4)对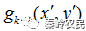
作逆傅里叶变换，得到
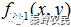，iFFT表示逆傅里叶变换。
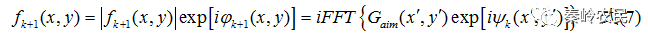
(5)将上一步获得的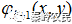
返回到步骤1，替换后继续进行迭代，重复上述步骤。
当均方误差SSE小于预先设定值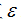
或迭代次数达到规定的最大迭代次数M时，得法停止。
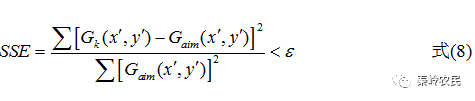
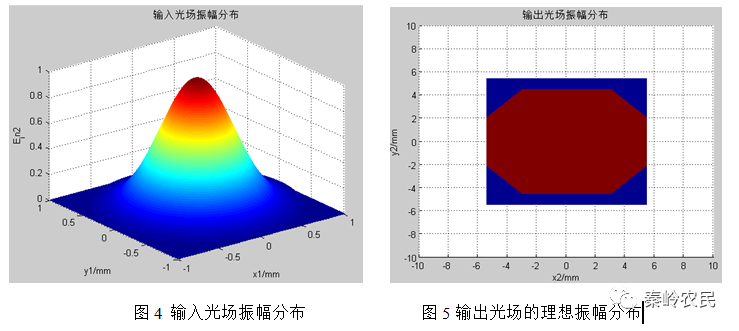
输入光波为高斯光束，其表达式为
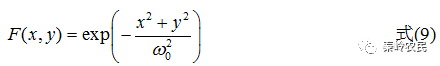
式中为高斯光束的束腰半径，取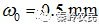
。
其它设计参数：
入射波长：523nm；
输入面与输出面间距：10mm；
DOE的大小：2*2mm2；
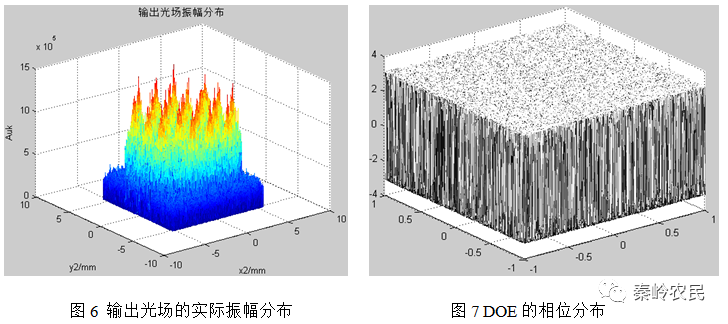
利用GS算法，通过合理设计，实现了从高斯光束到平顶光束的变化，MATLAB模拟的结果如图4-图7所示。
