1 声光效应
超声波通过介质时会造成介质的局部压缩和伸长而产生弹性效应,该应变随时间和空间作周期性变化,使介质出现疏密相间的现象,如同一个相位光栅,该光栅间距(光栅常数)等于声波波长λs。当光通过这一受到超声波扰动的介质时就会发生衍射现象。其衍射光的强度、频率、方向等都随着超声长的变化而变化。
声光介质中传播分为行波和驻波两种形式。设声波的角频率为ωs,波矢为κs,则沿x方向传播的声波方程为
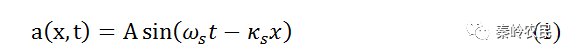
式中,a为介质质点的瞬间位移,A为质点位移的振幅。介质折射率的变化正比于介质质点沿x方向位移的变化率,即
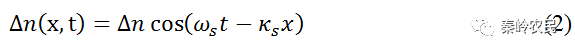
式中,Δn=-κsA。则声波为行波时的介质折射率
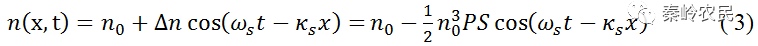
式中,S为超声波引起介质时产生的应变;P为材料的弹光系数。
超声驻波形成的折射率变化为
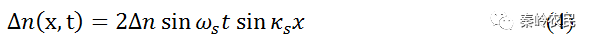
声驻波在一个周期内,介质两次出现疏密层,且在波节处密度保持不变,因而折射率每隔半个周期(Ts/2)就在波腹处变化一次,由极大(或极小)变为极小(或极大)。在两次变化的某一瞬间,介质各部分的折射率相同,相当于一个没有声场作用的均匀介质。若超声频率为fs,那么光栅出现和消失的次数则为2fs,因而光波通过该介质后所得的调制光的调制频率将为声频率的两倍。
按照声波频率的高低以及声波和光波作用长度的不同,声光相互作用可以分为拉曼—纳斯衍射和布拉格衍射两种类型。
2 布拉格(Bragg)衍射
当声波频率较高,声光作用长度L较大,而且光束与声波波面间以一定的角度斜入射时,光波在介质中要穿过多个声波面,故介质具有“体光栅”的性质。当入射光与声波面间夹角满足一定条件时,介质内各级衍射光会互相干涉,各高级衍射光将互相抵消,直出现0级和+1级(-1级)(视入射光的方向而定)衍射光,即产生布拉格衍射。
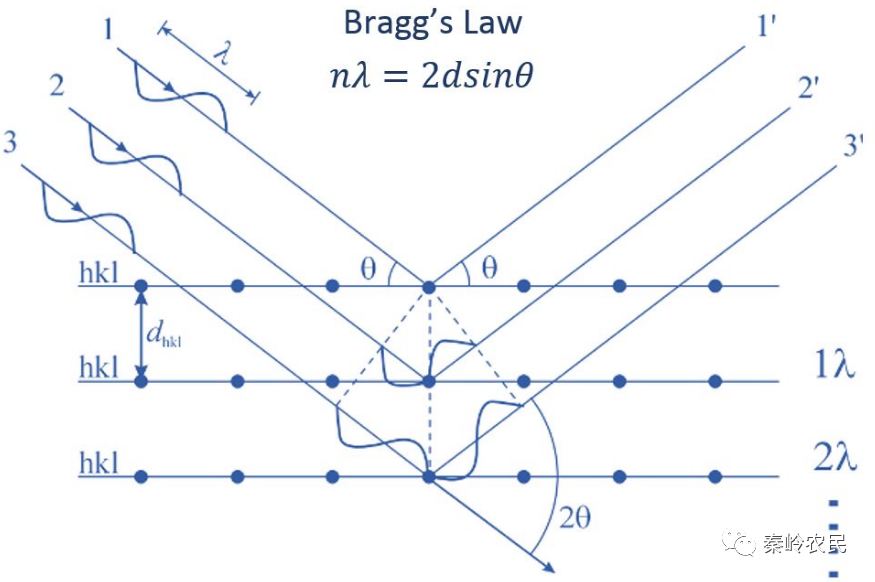
从波的干涉条件来推导布拉格方程。把光波通过的介质近似看成许多相距为λs的部分反射、部分透射的镜面。具体模型如下
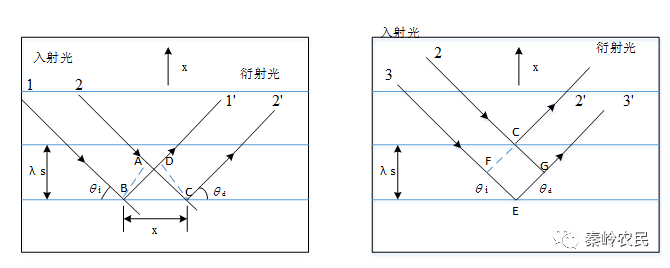
图1产生布拉格衍射条件的模型
如左图所示,不同光线在同一声波面上形成同相位衍射光束条件,即
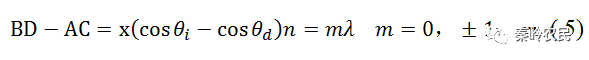
要使声波面上所有点同时满足这一条件,则有

即入射角等于衍射角。对于相距λs的两个不同镜面上的衍射情况,如上右图所示,若有C,E点反射的2’,3’光束具有同相位的条件,其光程差FE+EG必须等于光波波长的整数倍,即
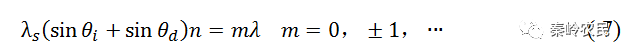
考虑到θi=θd,所以(m=1)

式中,θi=θd=θB,θB为布拉格衍射角。只有当入射角等于布拉格衍射角时,在声波面上衍射的光波才具有相同相位,满足相干加强的条件,得到衍射极值,称为布拉格方程。
由光的电磁理论可知,对于频率为ω的入射光,其布拉格衍射光的频率为ω±Ω。
3 布拉格衍射效率
在布拉格衍射时,衍射效率为
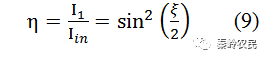
其中,ξ=2π/λ0ΔnL,在正常布拉格衍射时,声致折射率的变化Δn=-1/2n3pS。
由于超声波的平均能量密度为cS2/2=ρυs2S2/2,(其中c为介质的弹性劲度系数,S为应变,p为声光系数,与材料性质有关),则平均能流密度为ρυs3S2/2,再乘以换能器的面积HL(H,L分别为换能器的长度和宽度),即得超声波的能流或功率Ps为
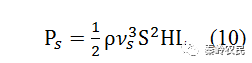
由上式关系可得
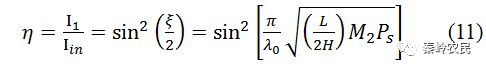
其中M2=n6p2/ρυs3,对于给定的声光材料和换能器,M2,L,H都是常量。当Ps改变时,η也随之改变。因而通过控制超声波功率Ps(即控制加在换能器上的电功率)就可达到控制衍射光光强的目的,这就是声光调制的原理。
由于Q正比于ΔkmL,故Q反应声光互作用的适配程度,作为声光互作用是否为布拉格衍射的定量标准。从耦合波方程可以看出,任意相邻两级衍射光之间(m和m-1级之间以及m和m+1之间)都通过声光互作用而相互耦合,因而当有零级光入射时,有可能得到各级衍射光。事实上由于入射光不能直接和二级以上的光耦合,所以仅当调整入射光的方向使Δk1(或Δk-1)=0时,即sinθi和
sinθB=ks/2ki=λ0/2nλs时,才能得到很强的±1级衍射光。
在产生布拉格衍射时,如果入射光的方向与声波的传播方向相反时且同时满足Δk1=0,此时产生+1级的衍射光;如果入射光的方向与声波的传播方向相同时且同时满足Δk-1=0,此时产生-1级的衍射光。
根据推正,当入射光强Ii时,布拉格声光衍射的0级和1级衍射光强表达式分别为
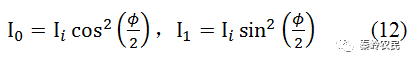
已知ϕ是光波穿过长度为L的超声场所产生的附加相位延迟,ϕ可以用声致折射率Δn的变化来表示,即
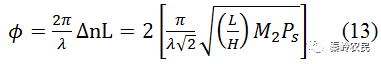
根据(13)式,在满足布拉格衍射的理想条件下,当入射光能量为I=1mJ,入射波长为λ=905nm,声光介质的品质因数为M2=35.6*10-15,换能器的长度为L=2.0cm,宽度为H=0.5cm时,利用matlab仿真衍射光强随超声波功率Ps的变化如图所示。
根据(13)式,在满足布拉格衍射的理想条件下,当入射光能量为I=1mJ,入射波长为λ=905nm,声光介质的品质因数为M2=35.6*10-15,换能器的长度为L=2.0cm,宽度为H=0.5cm时,利用matlab仿真衍射光强随超声波功率Ps的变化如图所示。
图中蓝线零级光的光强,红线为一级光的光强,从图中可知,随着Ps的增大1级光能量和0级光能量不断发生周期变化。当Ps足够大,使
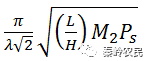
达到π/2时,1级衍射光达到最大,0级衍射光达到最小。
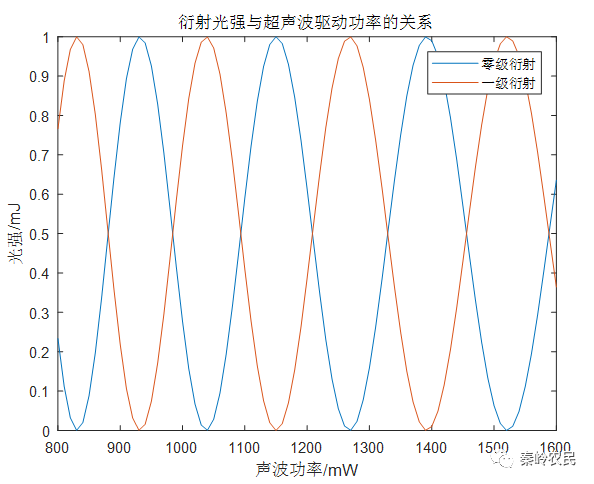
图2 I~Ps的关系
根据(12)式,当入射光能量为I=1mJ,声光介质的品质因数为M2=35.6*10-15,换能器的长度为L=2.0cm,宽度为H=0.5cm时,超声波功率在1.5W时,利用matlab仿真衍射光强随入射波长的变化如图所示。
从图中可知入射波长的不断增加衍射效率不断在发生周期性变化,说明波长的变化会破坏布拉格条件,太长的波长不满足布拉格衍射,导致衍射效率下降。从图中可以看处,超声波功率Ps=1.5W时,905nm的入射波长,其衍射效率可达82%左右。
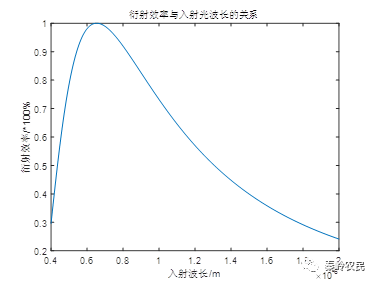
图3 η-λ的关系
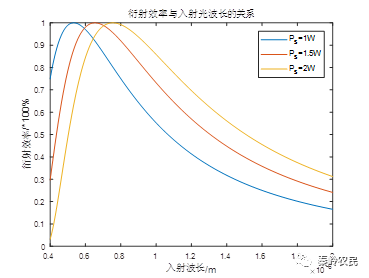
图4 超声波功率Ps不同时,η-λ的关系
对于一个声光扫描器来说,不仅要看偏转角Δθ的大小,主要的还要看其可分辨点数N。可分辨点数N定义为偏转角Δθ和入射光束本身发散角Δφ之比,即
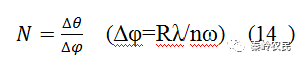
式中,ω为入射光束的宽度(光束的直径);R为常数,其值决定于所用光束的性质(均匀光束或高斯光束)和可分辨判据(瑞利判据或可分辨判据)。则扫描可分辨点数为

式中,ω/νs为超声波渡越时间,记为τ,也就是扫描器的偏转时间。故上式可以写成
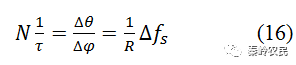
式中,N/τ为声光扫描器的容量—速度积,它表征单位时间内光束可以指向的可分辨位置数目,其表明,它仅取决于工作带宽Δfs,而与介质的性质无关。因此,当光束宽度和声速确定后,参数也就确定了。只有增加带宽才能提高扫描器的分辨率。
声光扫描器带宽受两种因素的限制,即受换能器带宽和布拉格带宽的限制。因为声频改变时,相应的布拉格角也要改变,其变化量为
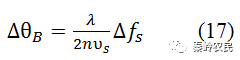
因此,要求声束和光束具有匹配的发散角。声光扫描器一般采用准直光,其发散角很小,所以要求声波的发散角δφ≥δθB。取δφ=λs/L,再考虑到(12),就得到
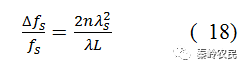
实际上,工作带宽的选取是由给定的指标N和τ确定的,此时工作频带的中心频率也已确定。因为正常布拉格器件的Q值一般不容易做得很大,故总存在一些剩余的高级衍射,此外还有各种非线性因素和驱动电源谐波分量的影响,为了避免在工作频带内出现假点,要求工作带宽的中心频率fs0≥3/2Δfs,或
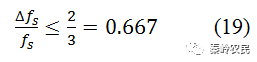
此式是设计布拉格声光偏扫描带宽的基本关系。