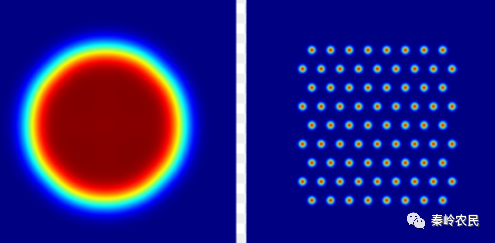
衍射光学元件(DiffractiveOptical Element，简称DOE)是一种基于光波衍射理论，利用计算机辅助设计，采用超大规模集成电路制造工艺在基片上或传统光学器件表面刻蚀出台阶或连续浮雕结构而形成的光学元件。
最早的DOE的应用是LordRayleigh在1871年所使用的振幅型菲涅尔波带片，随后1891年Wood研制出位相型菲涅尔波带片。1948年，D.Gabor提出了波前重现的全息原理，基于该理论，人们随后相继研究出了计算机制全息图以及相息图，但受制于当时的加工水平，其使用范围受到极大的限制。20世纪中叶以后，伴随着激光的出现和VLSI技术的使用，为台阶状位相结构的出现提供了可能。
二元光学技术的出现，解决了DOE的效率和加工问题，使得DOE进入高速发展时期。美国、加拿大、瑞士及德国的一些研究所和高校都相继开展了DOE的研究工作，美国的杜邦公司、以色列HOLO/OR公司、法国SILIOS公司也有相关的DOE产品研究。我国对衍射光学元件的研究起源于本世纪80年代，如80年代初期，中国科学院物理研究所的杨国祯和顾本源就提出了任意线性变换系统中振幅-相位恢复的一般理论及与之相关的杨-顾算法，并将它们成功用于解决多种实际问题和变换系统中。长春光机所在1992年就进行了将DOE应用于成像光学系统的研究。中国科学技术大学、清华大学、浙江大学、北京理工大学、国防科技大学、中国科学院光电技术研究所等许多单位也开展了DOE设计和加工方面的研究，并取得了许多卓越的成果。
对于“衍射”问题我们并不陌生，早在初中物理课本中就有接触。最初我们说，光在传播过程中绕过障碍物到阴影里继续传播的现象，叫做衍射。更广泛一些的说法是，当光在传播过程中遇到障碍物时偏离直线传播或偏离几何光学的传播规律，这种现象叫做衍射，如图1.1所示，光路上的障碍物被称为衍射屏。衍射现象有以下特点：(1)光束在衍射屏上的什么方位受到限制，则接收屏幕上的衍射图样就沿该方向扩展；(2)光孔的线度越小，对光束的限制越厉害，衍射效应越强。
对于单缝来说，单一方向的平行光垂直入射时，如果不发生衍射，在接收屏上看到的只是一个中央亮点(几何像点)，一旦发生衍射，在接收屏幕上接收到的是朝上下左右多个方向的衍射图样，如图1.2所示。
惠更斯-菲涅尔原理是研究衍射现象的理论基础，其基本思想为：波前上的每一点都可以看作新的次波源，发出次波，空间某一点P的振动是所有这些次波在该点相干迭加的结果。该理论成功的地方在于用“次波”的概念反映空间振动的传播，同时用“次波相干迭加”的思想将所有衍射情况引到统一的原理中来。“次波”和“次波相干迭加”由惠更斯和菲涅尔两人分别提出。
衍射系统由光源、衍射屏和接收屏组成。通常按它们相互间距离的大小，将衍射分为两类：一类是光源和接收屏幕(或两者之一)距离衍射屏有限远，这类衍
射叫做菲涅尔衍射；另一类是光源和接收屏都距离衍射屏无穷远，这类衍射叫做夫琅禾费衍射。菲涅尔衍射是普遍存在的，而夫琅禾费衍射是菲涅尔衍射的一个特例。但由于夫琅禾费衍射计算简单得多，因此人们把它单独归为一类进行研究，尤其在傅里叶变换光学中，实际中有很多夫琅禾费衍射装置的变型。
傅里叶变换光学是现代光学的重要分支，它以经典波动光学原理为基础，是对干涉和衍射的综合与提高，尤其与夫琅禾费衍射息息相关。现代变换光学从变换的角度又对衍射和衍射屏做了更深入的分析。
当光在传播过程中，由于种种原因而改变了波前的复振幅分布(包括振幅分布或相位分布)，后场不再是自由传播时的光波场，这便是菲涅耳-基尔霍夫衍射积分公式对衍射的解释。凡能使波前上复振幅发生改变的物，统称为衍射屏，其作用是破坏原有自由空间的波前并重新构建波前，从而使衍射场重新分布。DOE在光路中起衍射屏的作用。
以衍射屏为界，整个衍射系统被分为前后两个部分，前场为照明空间，充满照明光波场；后场为衍射空间，充满衍射光波场。照明光波一般为球面波或平面波，它们的等相面和等幅面是重合的，其在波场中没有因强度起伏而出现的亮暗图样。衍射波则比较复杂，不是单纯的球面波或平面波，其等相面和等幅面一般不重合，属于非均匀波，波场中有因强度起伏而形成的衍射图样。
在一个衍射系统中，如图1.3所示，有三个波前上的场分布是需要特别考虑的，分别为：(1)衍射屏之前的照明光波前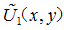
，称为入射场；(2)衍射屏之后的衍射光波前
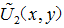，称为透射场；(3)接收屏上的光波前
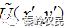，称为接收场。把波前U1转化为波前U2是衍射屏的作用，从波前U2导出波前U是光的传播问题。两部合起来成为衍射。因此，也可以说，衍射就是波前的变换。
衍射屏的作用可以用屏函数来表征：
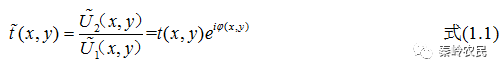
对于透射屏来说，屏函数称为复振幅透过率函数。屏函数一般也为复数，包括模和辐角两部分，在(1.1)式中，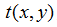
是振幅模函数，
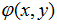是辐角函数。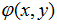为常数的衍射屏称为振幅型的；
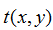为常数的衍射屏称为相位型的
任何形状的孔或遮光屏是最简单的振幅型衍射屏，其屏函数的形式为
透镜是最常见的位相型衍射屏，其透过率函数为：
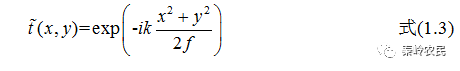
上式中 f 为透镜的焦距。平行于光轴的单色平行光束入射在透镜上，在透镜后其透射场函数为：
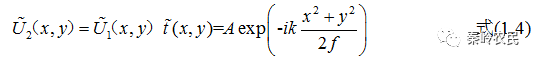
对于正入射的平面波，有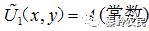
，由相因子可知，后场中的光波场是会聚到透镜后距离为处的球面波。与几何光学理论一致。
在数学上可以将一个复杂的函数作傅里叶展开，从这种观点出发，可以认为一张复杂的图片是由许多不同空间频率(空间频率指光波场沿波失K方向每增加单位长度，光波场增加的周期数)的单信息组成的。
对于屏函数是严格周期性函数的衍射屏(透射式或反射式)，统称为光栅，对于周期为d的一维光栅，其屏函数只依赖一个坐标变量x，对于任一x，有
周期函数的傅里叶级数展开通常有三种形式：
(1)正弦余弦式
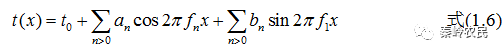
式中n为整数，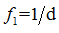
是基频，
是基频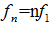的整数倍，称为n次谐波的频率，上式中后两项皆对所有正整数求和。傅里叶系数由积分式给出：
(2)余弦相位式(见图1.4)
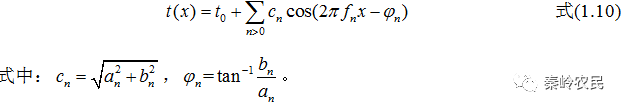
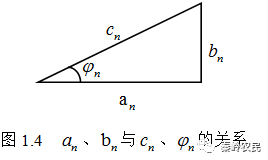
(3)指数式
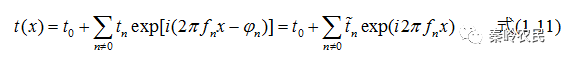
上式中第二项是对所有非零整数的求和，式中复傅里叶系数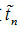
可由积分式给出：
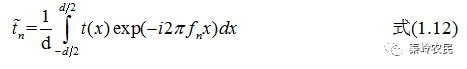
由(1.12)式可以看出，复傅里叶系数 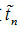的集合可以告诉我们原函数
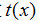中各空间频率的成分占多大的比例，通常把这叫做傅里叶频谱，或简称频谱。一般来说，频谱可以是连续的，也可以是分立的(只取某些分立值)。但由上述分析可知，周期函数展成傅里叶级数，其频率只取基频
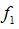的整数倍，故周期函数的频谱总是分立的。以下将以黑白光栅为例，详细介绍该过程。
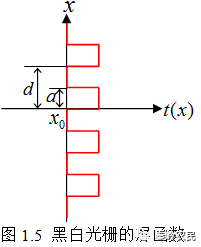
图1.5给出黑白光栅(一维)的屏函数。按照已有的知识，一个函数具有严格的周期性，对于任意x,它的屏函数有如下性质：
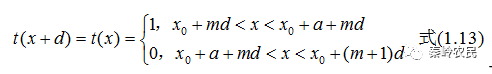
对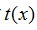
作傅里叶级数展开，得
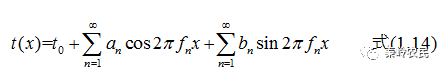
式中n为整数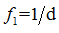，是基频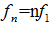，是基频的整数倍，称为n次谐波的频率，上式中后两项皆对所有正整数求和。傅里叶系数由积分式给出：
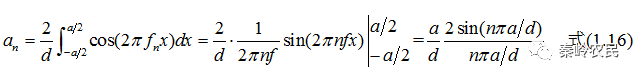
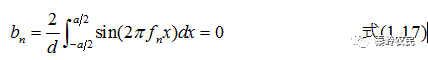
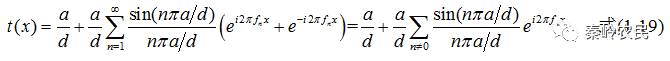
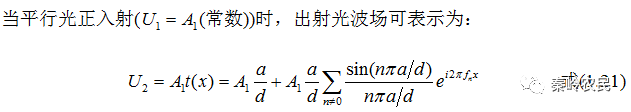
因此，n级主极强的光强
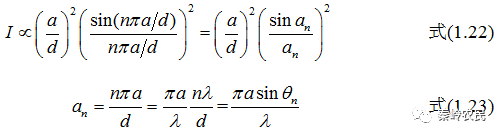
公式(1.22)中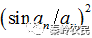 
正是多缝衍射中的单缝衍射因子，可见n级主极强的光强正比于单缝衍射因子。
设光栅周期与单缝宽度之间满足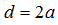
，则公式(1.21)变为：
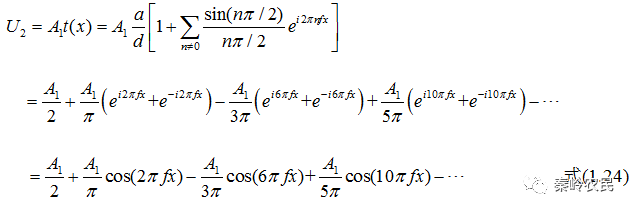
第n级衍射光的衍射角满足公式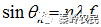
，从计算结果不难看出，黑白光栅的衍射谱是分立的。
当输入面与输出面间的距离L满足：
利用夫琅禾费衍射积分公式可得输出面上的光场分布：
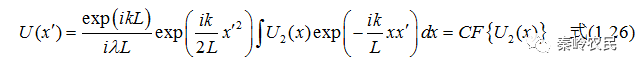
上式中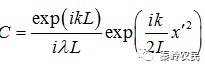
，由上式可得出结论：夫琅禾费衍射场是屏函数的傅里叶变换式。
傅里叶变换光学赋予夫琅禾费衍射新的意义，即理想的夫琅禾费衍射衍射系统是一种傅里叶频谱分析器。当单色光正入射在待分析的图像(具有特定相位分布的DOE)时，通过夫琅禾费衍射，一定空间频率的信息就被一对特定方向的平面衍射波输送出来。这些衍射波在近场区彼此交织在一起，到了远场区它们彼此分离，从而达到“分频”的目的，如图1.6所示。
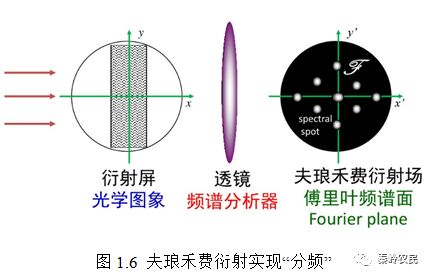
通过夫琅禾费衍射的傅里叶变换实现“分频”的基本思想可描述为：
(1)将波前上所有点源出的次波中具有相同传播方向的成分集合在一起，各球面次波中不同传播方向的成分分别构成不同方向的平面波分量。这些不同方向的平面波分量代表着波前上包含的不同空间频率成分。
(2)任何一个复杂单色场的波前，都可以看作一系列具有不同振幅和传播方向的基元单色平面波的叠加。当单色波入射到衍射屏上时，通过夫琅禾费衍射衍射系统，一定空间频率的信息就被一定特定方向的平面波衍射出来。
