
信号的奈奎斯特(Nyquist)频率定义为频谱受限信号的最高频率两倍。假设信号 的奈奎斯特频率为 ,求下面信号的奈奎斯特频率:
(1)

(2)

(3)

(4)

(5)

已知两个信号 都是频谱受限信号,它们各自最大角频率为 ,且 。设:
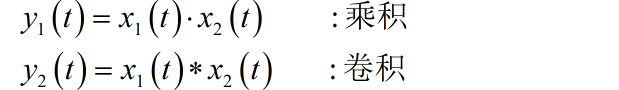
利用周期为 T 的周期冲激信号 分别乘以 ,得到采样信号 。
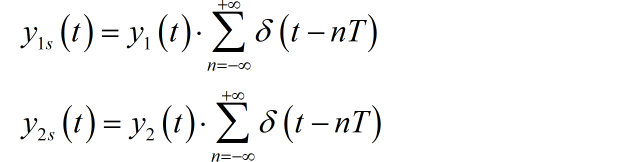
给出能够从 中恢复出 对应的最大采样间隔 。
提示: 这个选做题绕了很大一个圈子,实际上是询问 的最大频率,或者对应的 奈奎斯特频率。
已知信号 的表达式为:
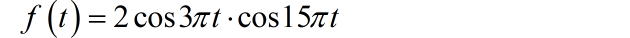
使用采样频率 对该信号进行采样。
(1) 绘制出 的频谱;
(2) 会知识采样信号 的频谱;
(3) 使用理想低通滤波器从采样信号中无失真恢复出 ,求该低通滤波器带宽的范围。
(4) 信号 对应的奈奎斯特频率是多少?
已知信号 的频谱为 ,如下图所示:
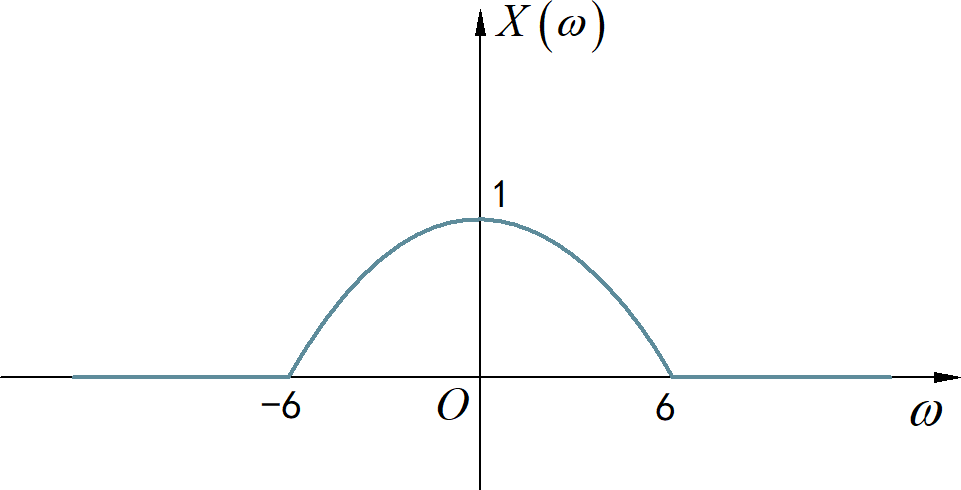
注: 上面频谱中频率为信号对应的角频率。
(1) 求 和 对应的奈奎斯特频率,既个信号最高频率的 2倍。
(2) 利用周期脉冲信号 对 进行采样,其中:
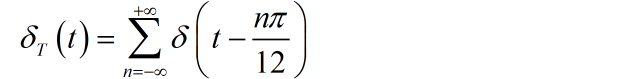
绘制采样后信号 的频谱,并判断是否发生了频率混叠。
已知信号处理系统如下图所示:
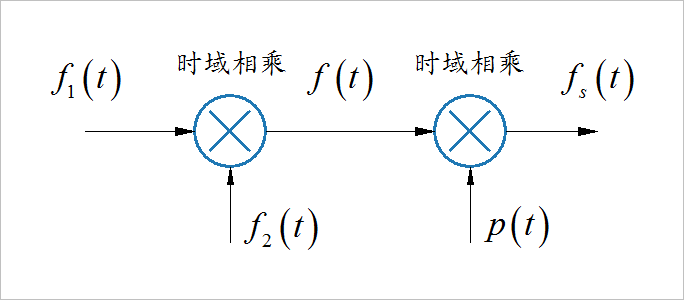
系统中的各个信号为:
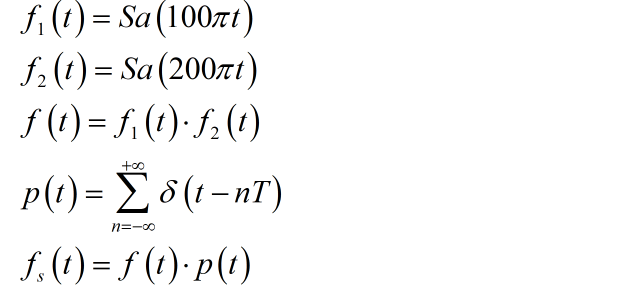
(1) 为了从 中无失真恢复出 ,写出最大抽样间隔 。
(2) 当 时,绘制出 的频谱的幅度谱 。
信号 的最高频率为 ,其频谱为 ,如下图所示:
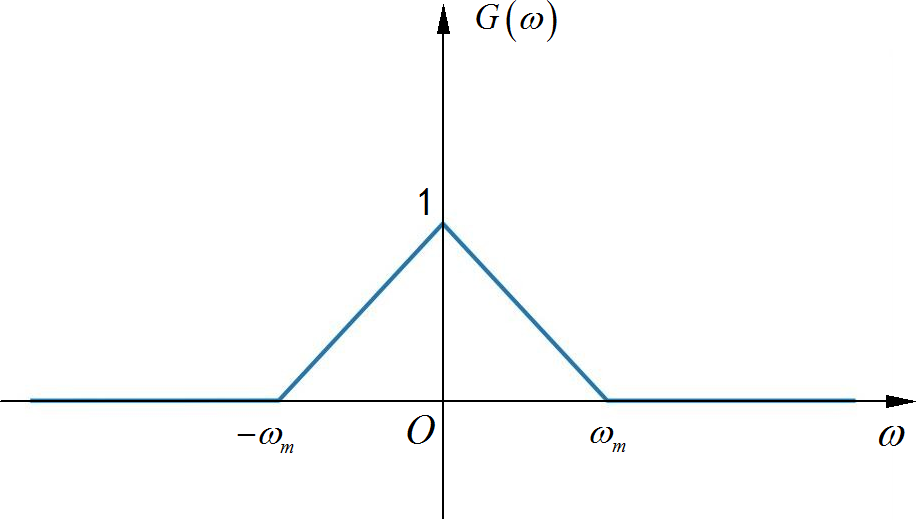
▲ 图1.2.1 信号gm(t) 的频谱使用下面所示的周期矩形脉冲信号 对 进行平顶采样,也就是采样后的矩形脉冲顶部是一个恒定值,与中心时间 对应的信号赋值 相同。
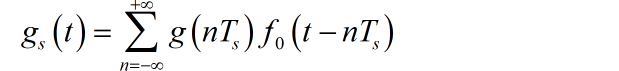
其中 就是周期矩形采样信号在一个周期内对应的矩形脉冲信号。它可以表示成:
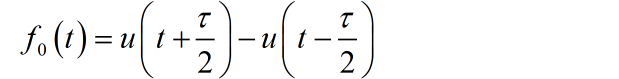
(1) 求采样后信号 的频谱表达式,并大体绘制出频谱图;
(2) 给出从 无失真恢复 的条件和方法;
提示: 今年这道系统与去年有区别,所使用的是矩形脉冲进行平顶采样。
已知实数信号 的频谱分布在一个有限频带内, ,如下图所示。假设信号的待会 是其最高频率 的 N 分之一,也就是:

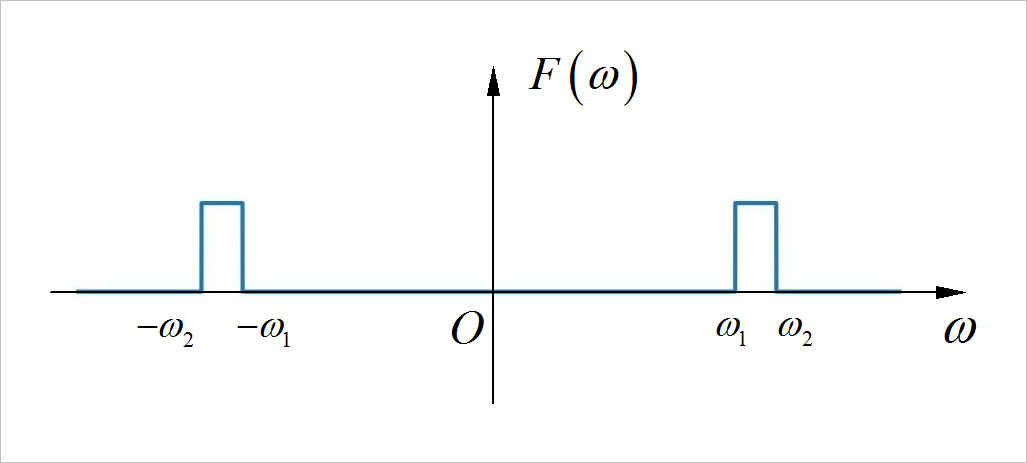
▲ 图1.3.1 有限窄带信号频谱示意图注: 上面仅仅是有限带宽信号频谱示意图,并不代表信号频谱是两个矩形脉冲。
试分析对该信号进行无损采样的最低频率是多少? 给出信号恢复出原始信号 的过程。
□ 必做题
已知频谱为 5MHz 的正弦波,被 25MHz 采样后,使用 零阶保持进行恢复。
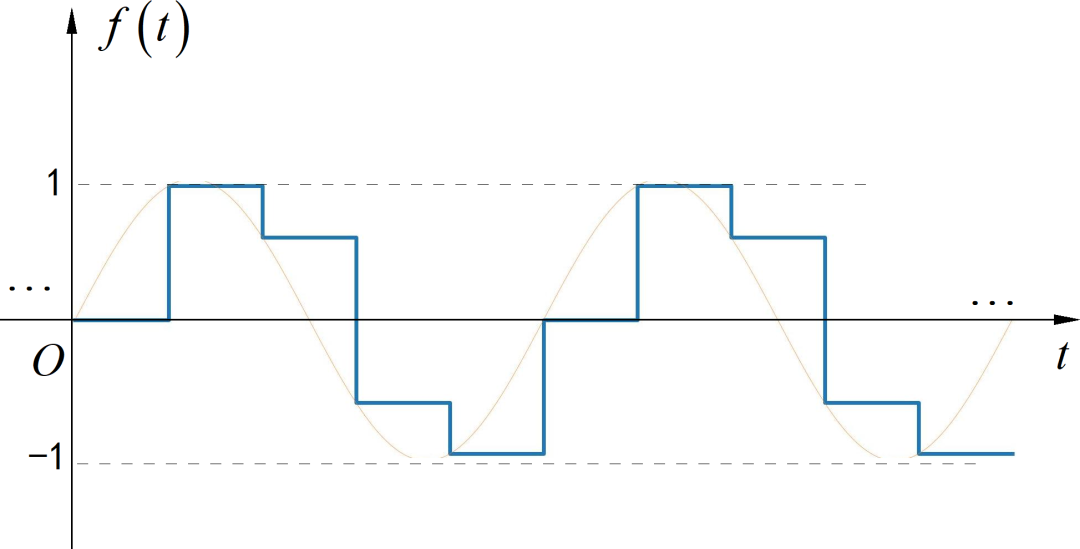
▲ 图1.1.1 零阶采样保持信号波形(1) 请写出零阶保持输出的频谱,并粗略绘制出恢复信号频谱;
(2) 如果从上述 零阶保持恢复波形中,恢复原来的 5MHz 的正弦波,请写出补偿滤波器的频谱特性。

▲ 图1.1.2 补偿低通滤波器输出设三角形和升余弦信号的底宽都是 , 使用抽样间隔 进行采样,分别绘制出两个信号被采样后的频谱。
□ 选做题
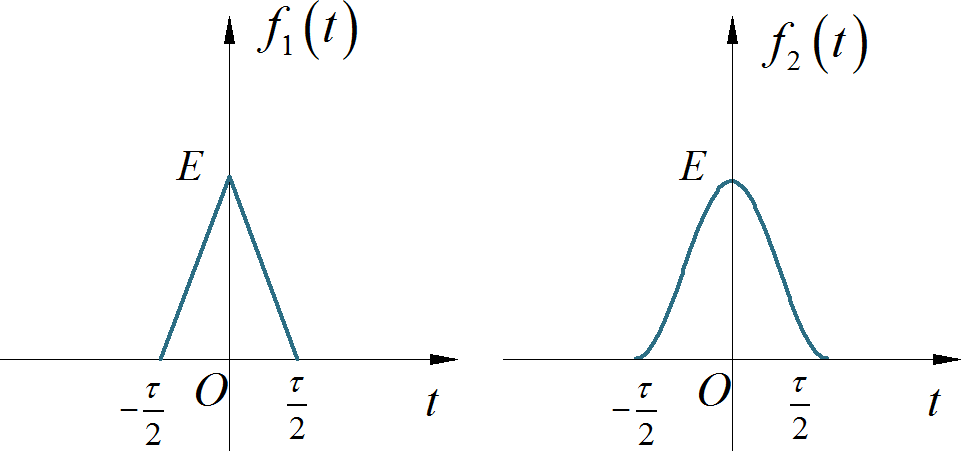
▲ 图1.1.3 三角形与升余弦脉冲信号使用计算机产生一个高斯信号单边带(上边带)调制信号。故意选择载波频率 比较小,使得正弦调制下会产生频率混叠。
(1) 上边带调整采用 移相法 产生。验证一下是否这种调制方式所产生的单片带调制信号不会产生 “频率混叠” 现象
(2) 设计一个流程,能够从上边带调制信号中恢复出原来的高斯信号。
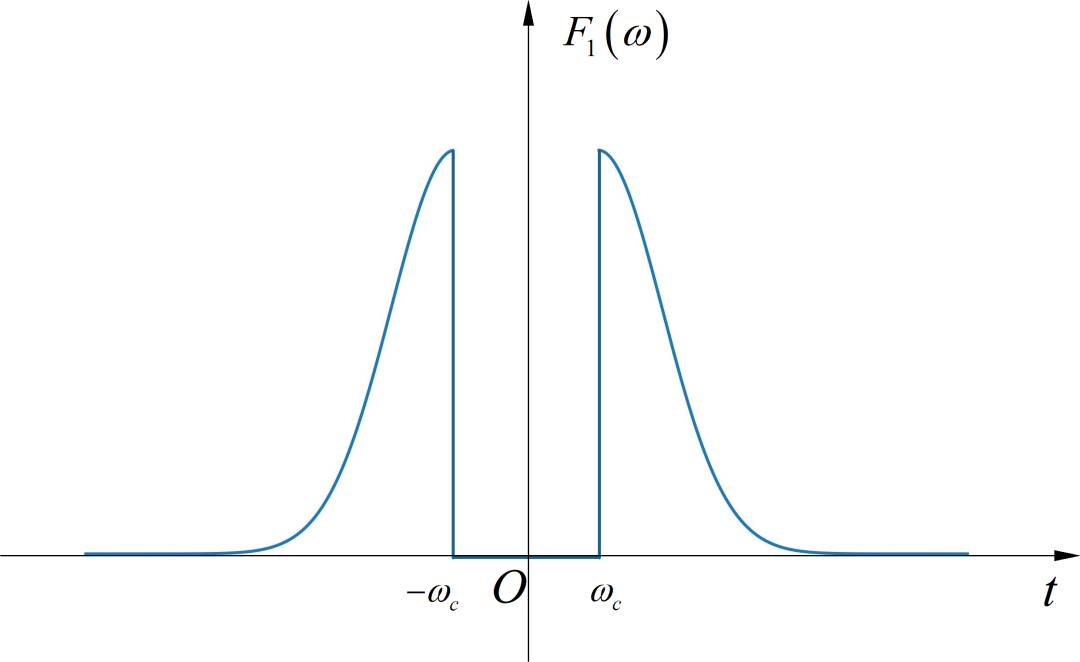
▲ 图2.1.1 高斯信号上边带调制的频谱信号与系统2024(春季)作业要求以及参考答案汇总: https://zhuoqing.blog.csdn.net/article/details/136798840
[2]信号与系统 2023年春季学期期末考试命题: https://zhuoqing.blog.csdn.net/article/details/131068697
[3]信号与系统期末2024年春季学期期末考试命题-模拟考试: https://zhuoqing.blog.csdn.net/article/details/139587106
[4]信号与系统期末2024年春季学期期末考试命题-正式考试试题: https://blog.csdn.net/zhuoqingjoking97298/article/details/139640739?csdn_share_tail=%7B%22type%22%3A%22blog%22%2C%22rType%22%3A%22article%22%2C%22rId%22%3A%22139640739%22%2C%22source%22%3A%22zhuoqingjoking97298%22%7D
[5]信号与系统2025(春季)作业要求及参考答案汇总: https://zhuoqing.blog.csdn.net/article/details/145879368