电路单位冲激响应仿真

• impulse — SciPy v1.15.2 Manual^[1]

01 冲激响应

一、前言

  第三次作业中，第二个题目是对RLC谐振电路进行系统仿真。得到不同串联电阻下，电路的单位冲激响应信号。下面应用 scipy  软件包中的 impulse 函数，来求取该线性电路的单位冲激响应。

二、impulse

  根据 impulse 函数的说明，使用它需要输入系统模型参数。可以使用四种系统模型，其中第二种，即系统函数的分子、分母系数最为简单，可以直接通过描述系统的微分方程来得到。 下面的几个参数分别给出了系统的初始条件以及时间参数。具体的函数使用方法在这里就不展开了。大家可以根据 后面给出的程序来进行琢磨。

三、建立系统模型

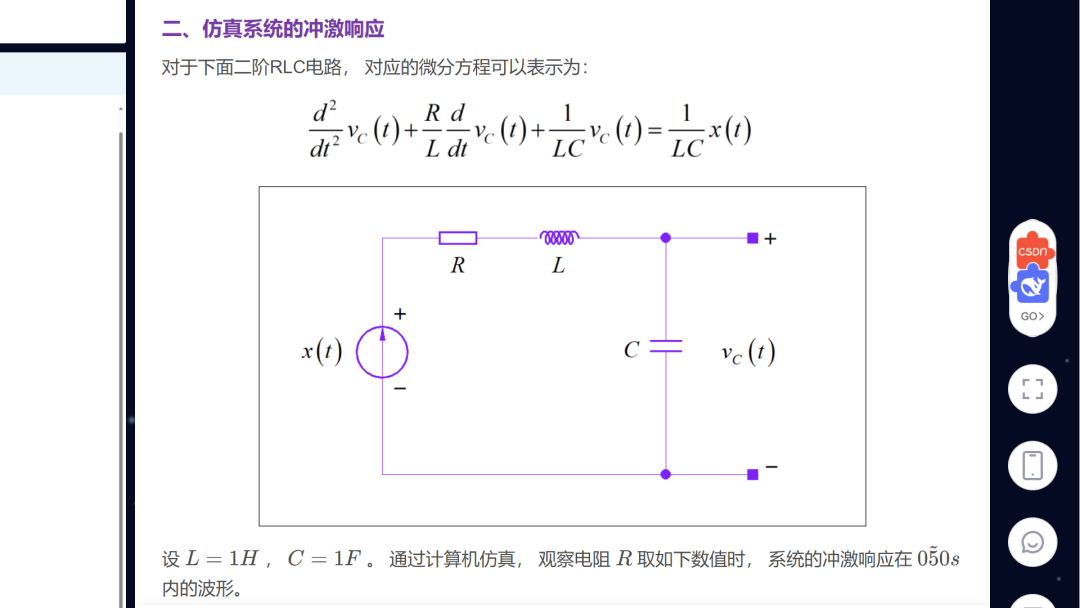
  根据题目内容，  按照其中微分方程，写出拉普拉斯变换之后对应的代数方程。这一点在现在教学课程还没有讲到，可以先将它看成算子方法的一个扩展。也就是将微分使用变量s来替换。这样便可以得到输出与输入的比值， 得到的这个比值实际上就是表述系统的系统函数。在这里，我们关心的是 SCIPY 软件包中所需要的系统描述中的一种，也就是系统函数有理分式的分子和分母，利用它，便可以调用 impulse 函数，得到系统的单位冲激响应了。

五、仿真结果

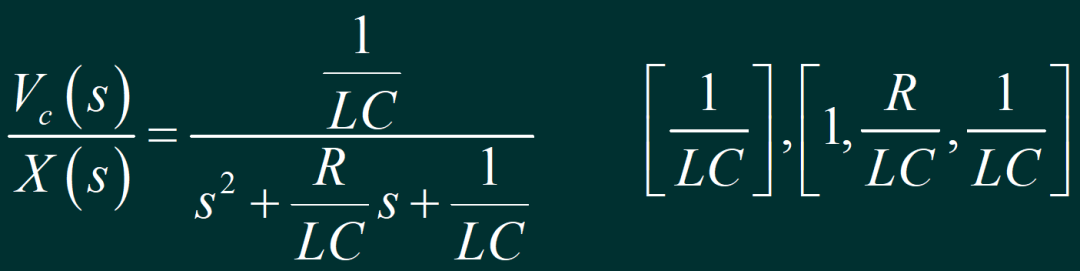
  运行程序之后，可以得到 0 到 50 秒之内的电路仿真输出信号 。可以看到，随着谐振电路中的串联电阻的增加，输出信号震荡减小。当电阻等于0，电路的单位冲激响应为等幅正弦震荡信号。当串联电阻等于0.2 欧姆的时候，输出为指数衰减震荡信号。当串联电阻为 2欧姆的时候，输出信号中不再震荡，当电阻等于5欧姆的时候，输出信号进一步减小。

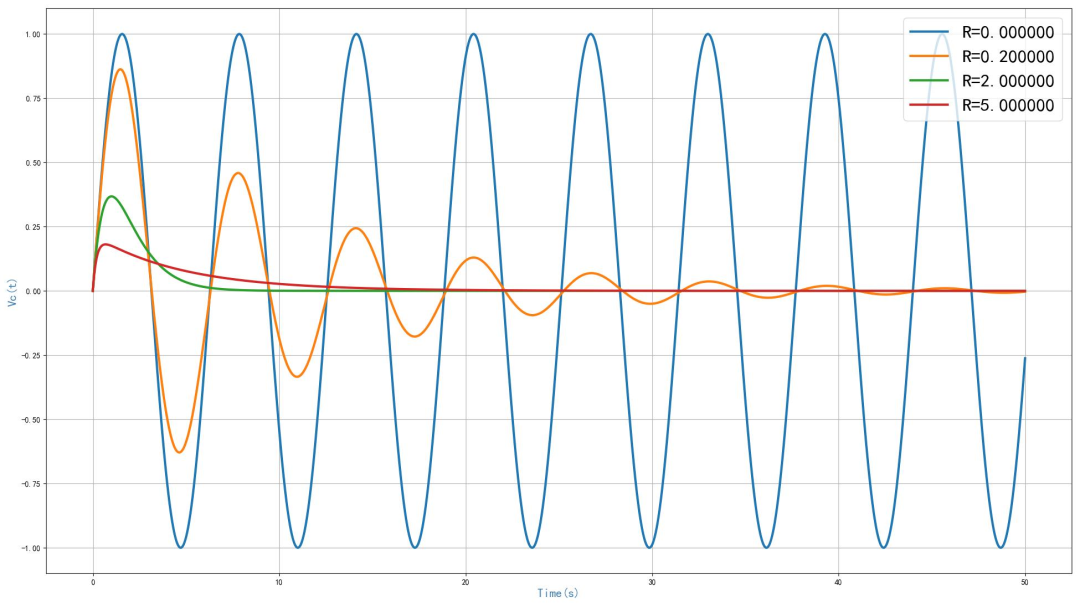
  不同的电阻，震荡周期都是相同，通过波形可以看到，周期大约为 2π，这与系统对应的谐振频率是对应的。电路中的电感和电容的数值都是1，由此，可以知道输出信号震荡周期为 2π。

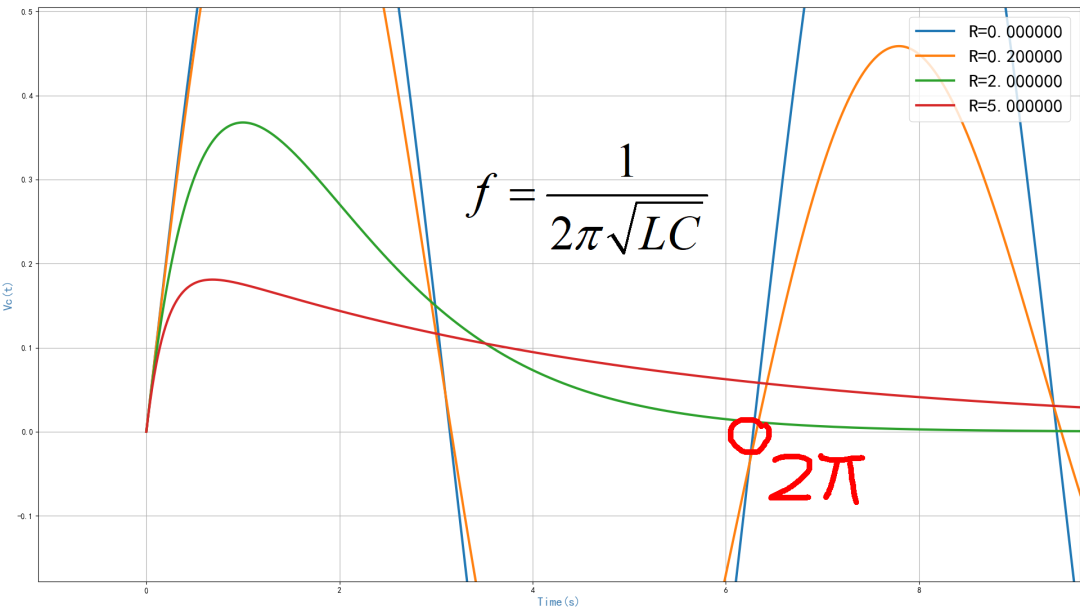
  通过仿真，可以看到，电路中的串联电阻可以影响单位冲激响应输出波形。随着电阻的增加，输出信号从震荡转换到不震荡，输出信号的幅度也会下降。通过理论分析，可以得到一个临界点，也就是对应输出信号从震荡转换到不震荡对应的串联电阻的数值。

※ 总  结 ※

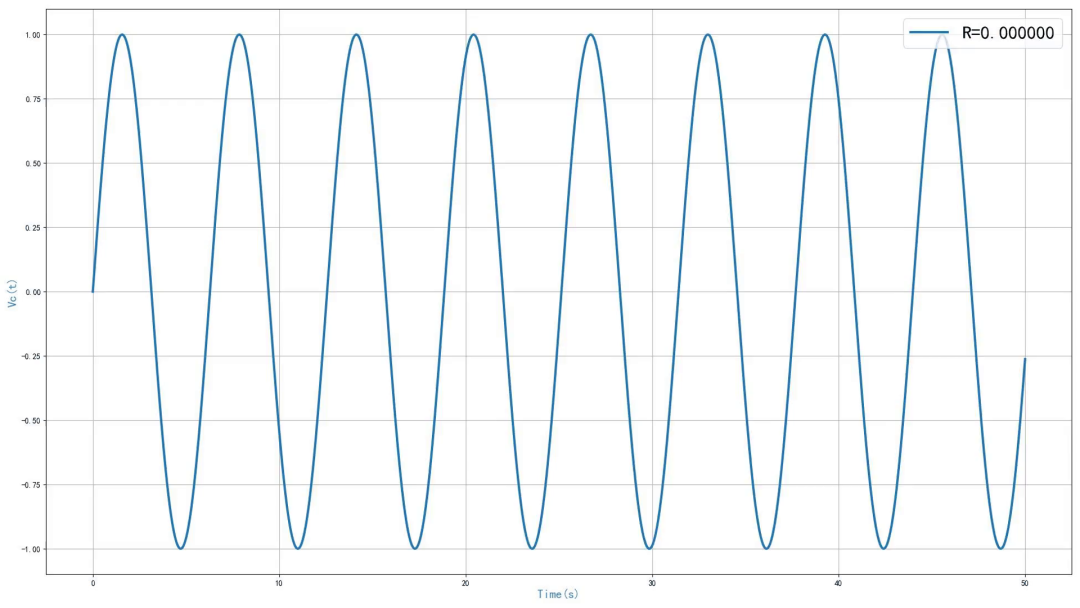
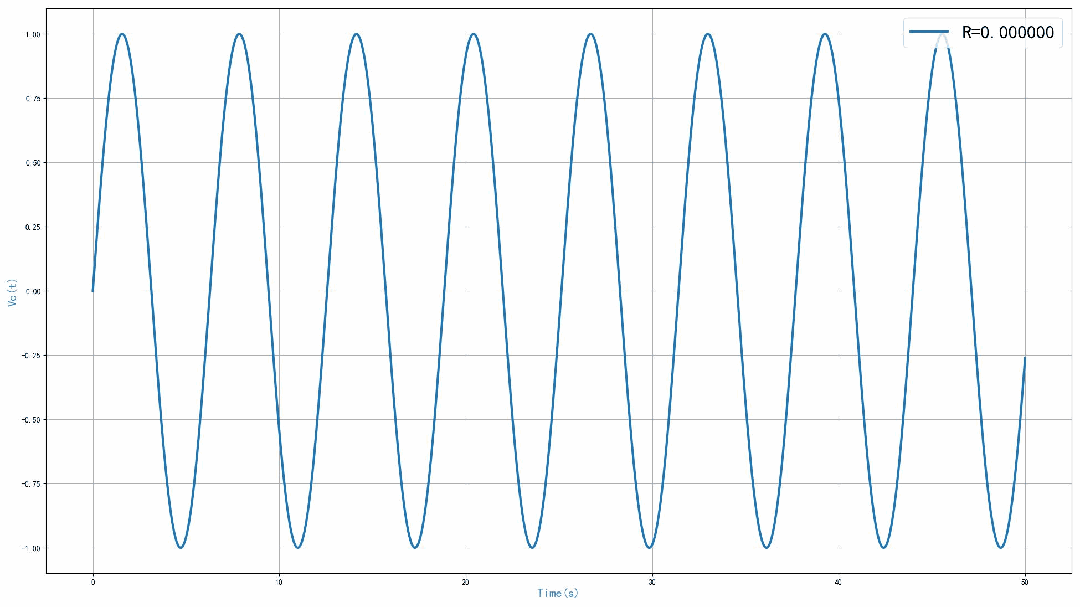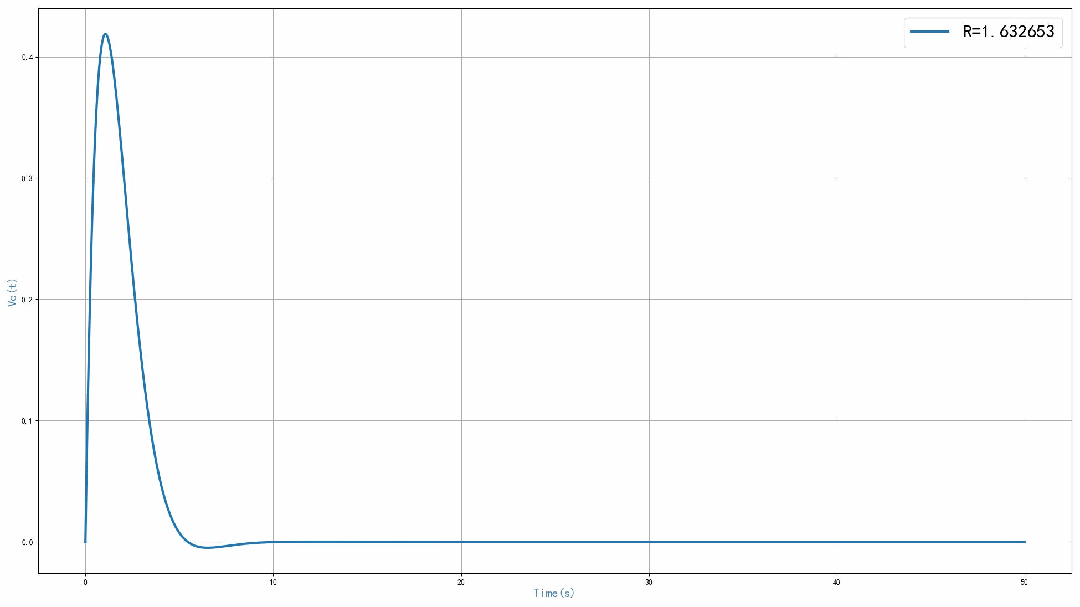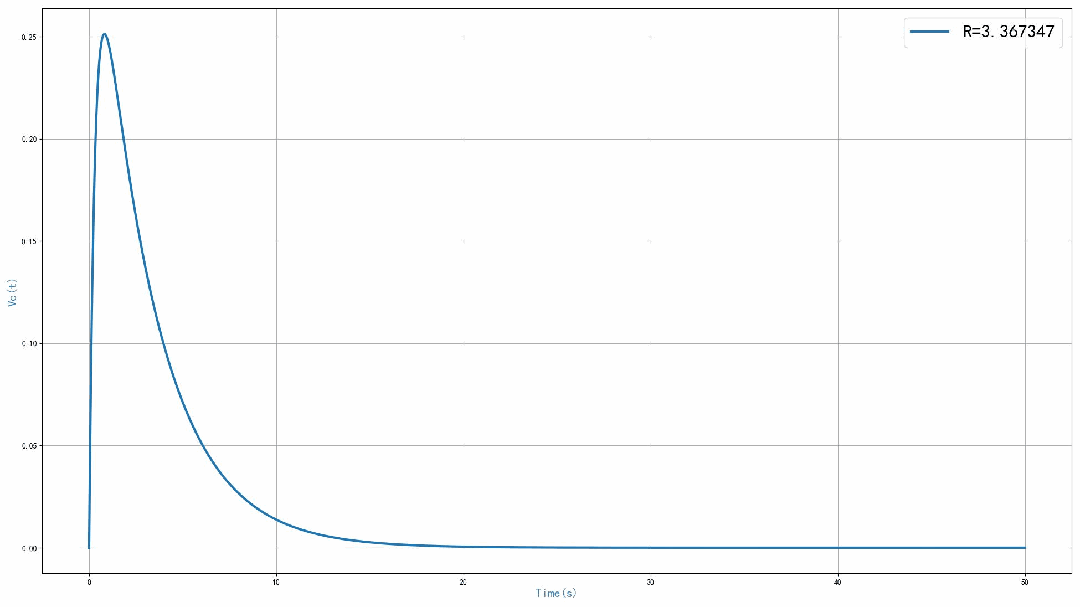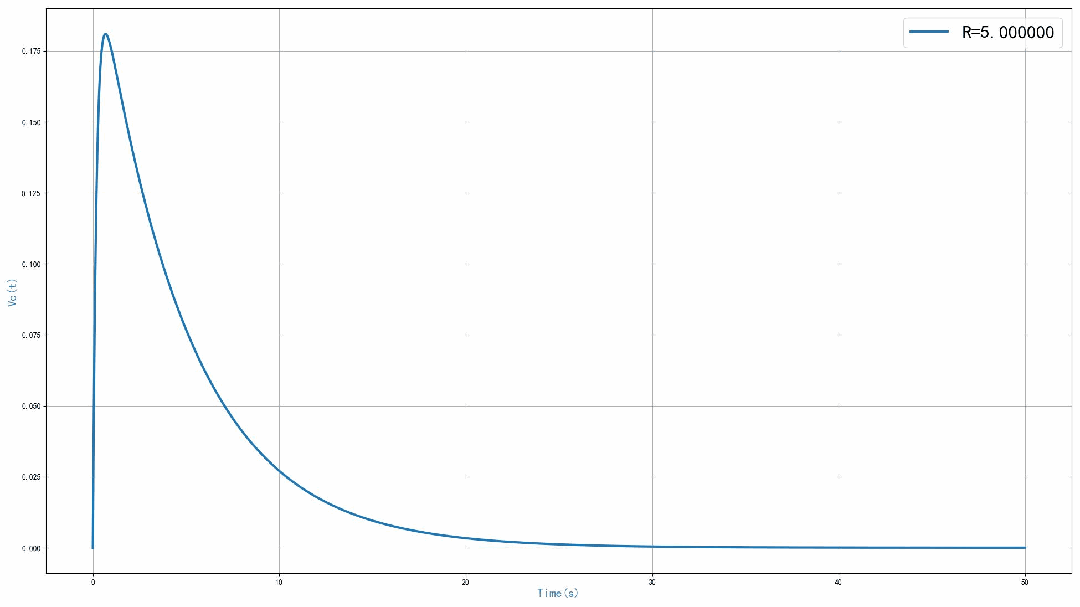
  本文对于第三次作业中的系统冲激响应仿真实验进行了讨论。相应的Python代码在CSDN对应的博文中给出了。