
(1)第一小题
■ 解答:
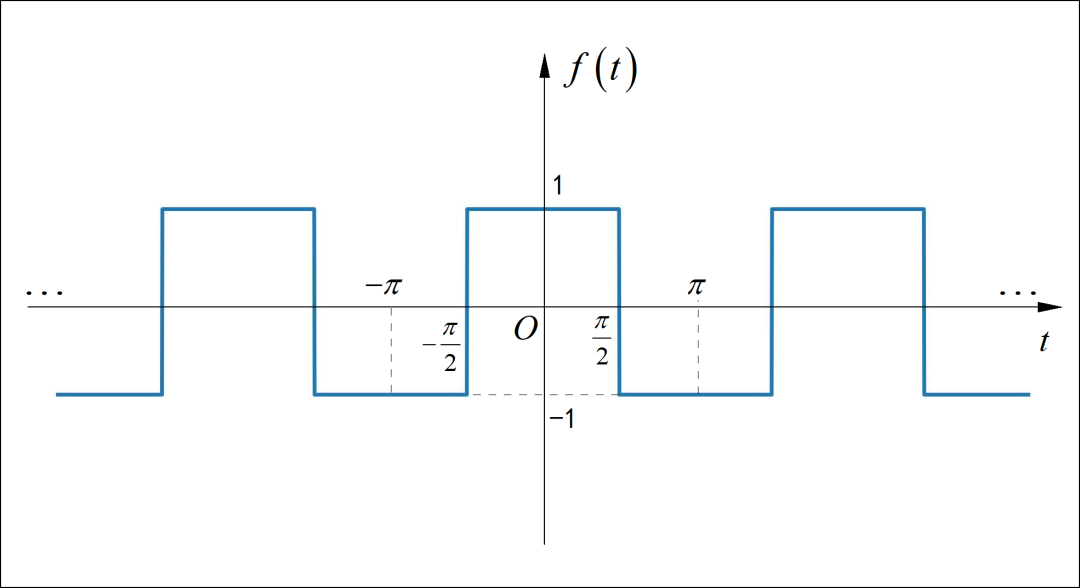
信号是偶对称,所以它只存在 cos分量 系数,sin分量系数 。信号的周期 ,则 。
(1)
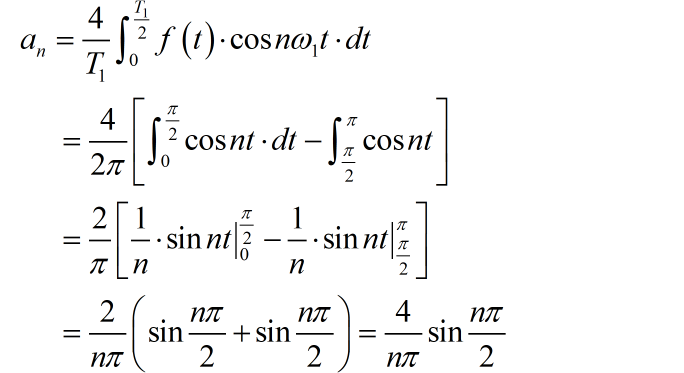

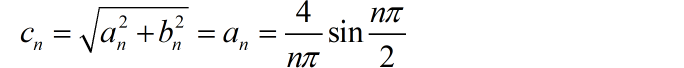

(2)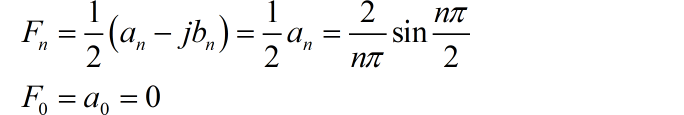
(3)
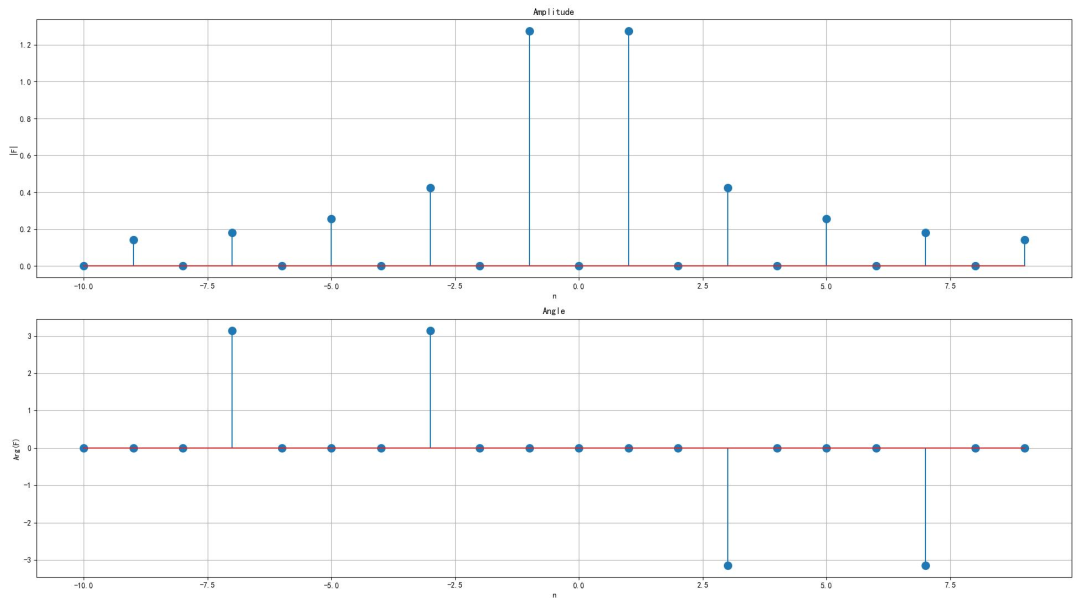
▲ 图1.1.1 幅度谱和相位谱(2)第二小题
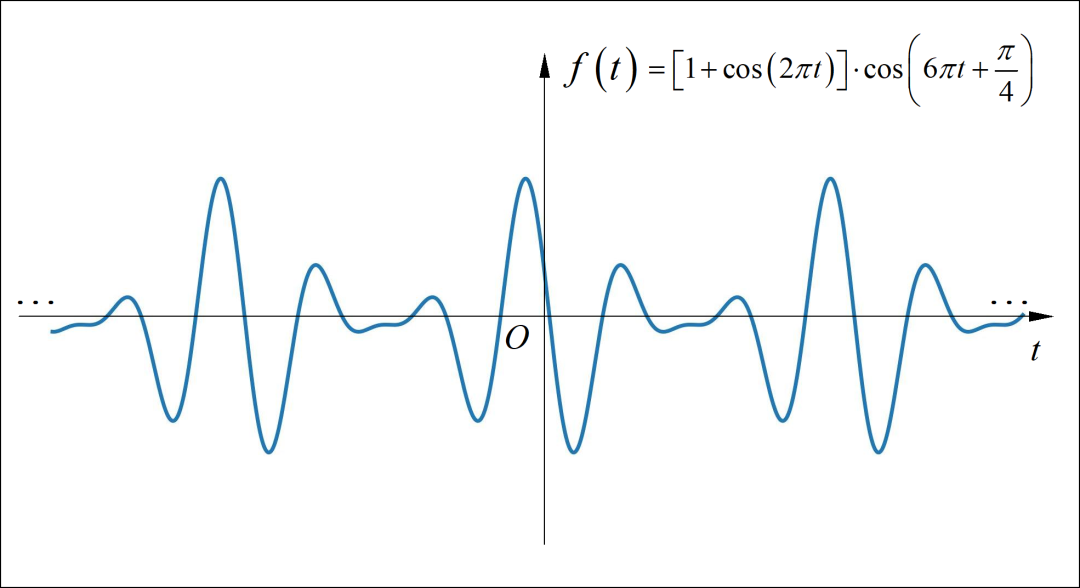
■ 解答:
(1)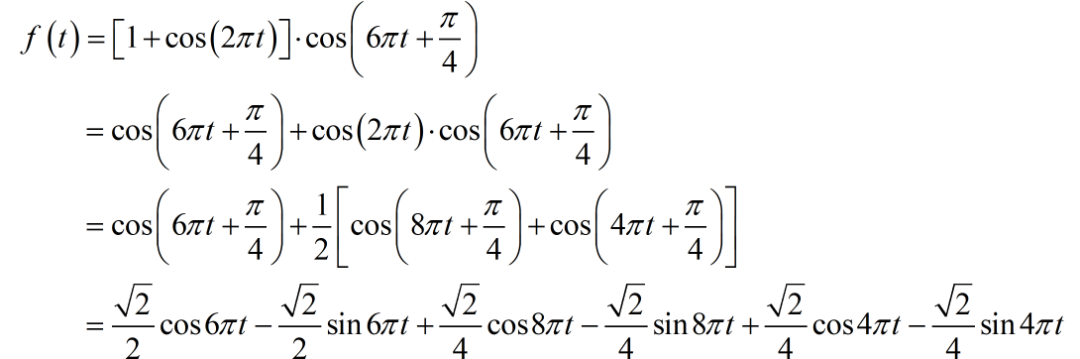
信号的基频 ,它进行傅里叶级数分解,只包含有有限项,各自的系数如下:
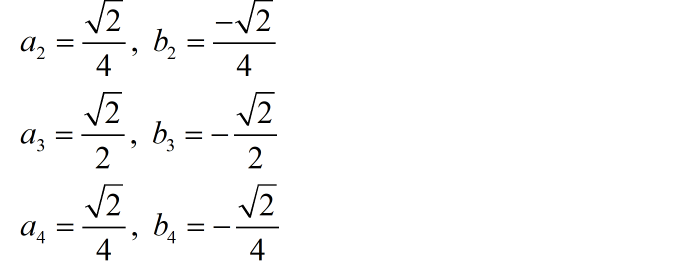

(2)
中只包含有有限项,它们各自系数如下:
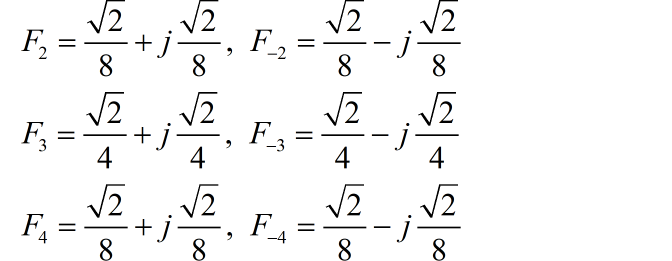
(3)
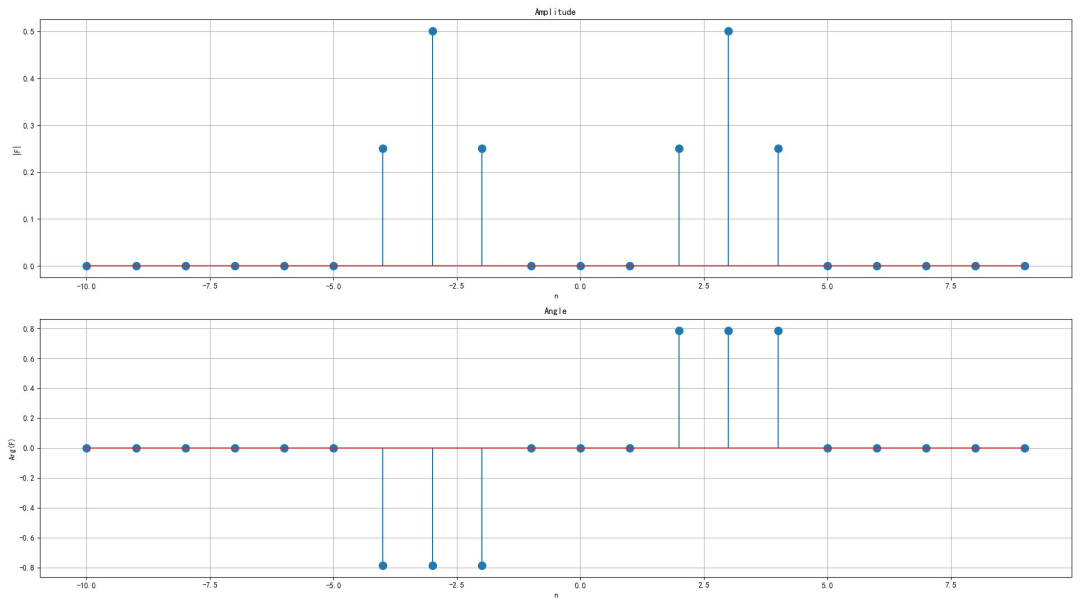
▲ 图1.1.2 信号的双边频谱(3)第三小题
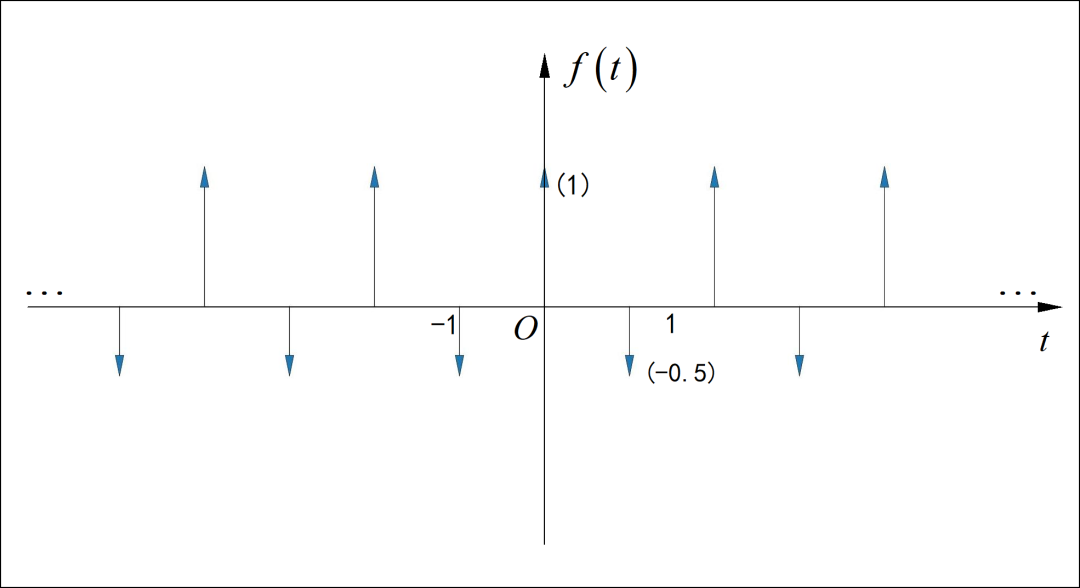
■ 解答:
(1)
信号的周期 , 。信号为偶对称函数,所以只包含有 cos 系数, ,sin项系数 都为 0。
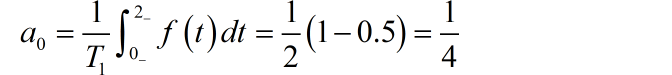
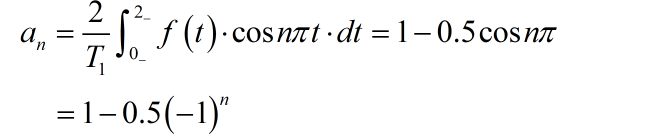

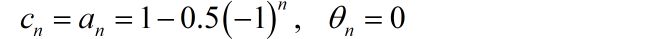
(2)

(3)
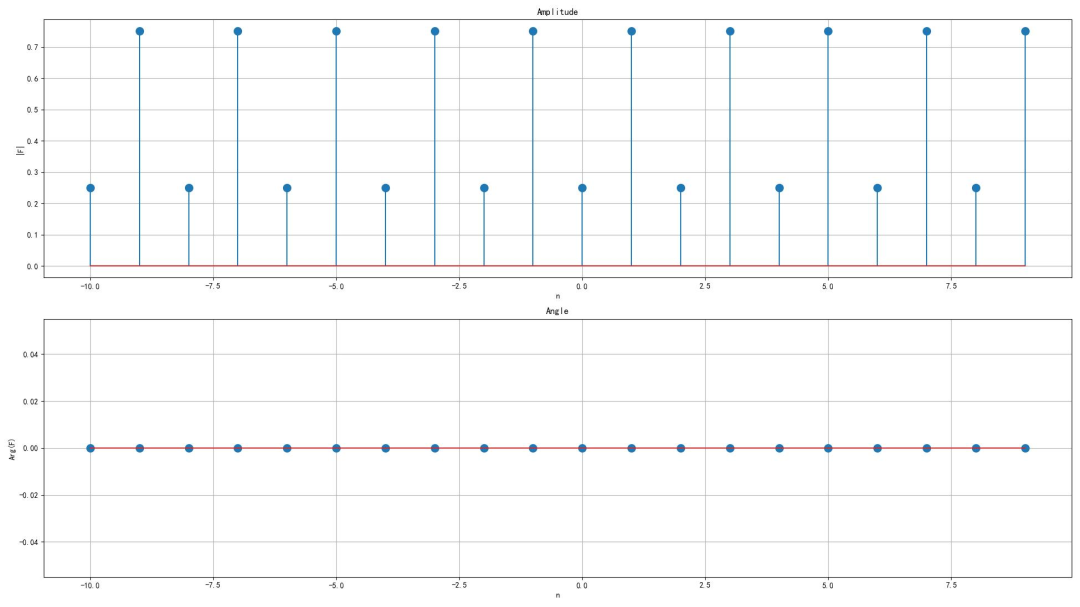
▲ 图1.1.3 信号的双边频谱(4)第四小题
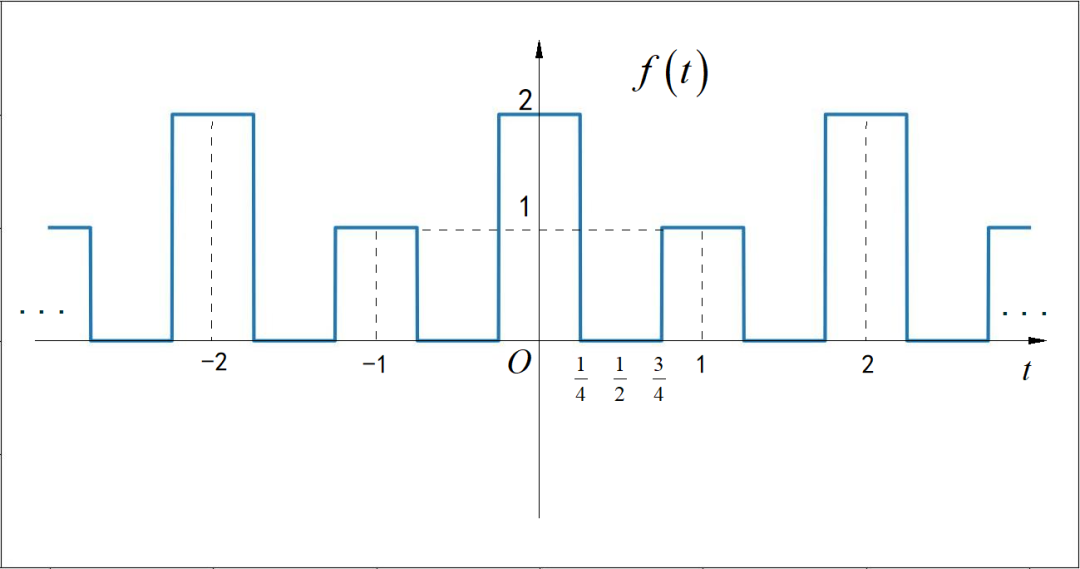
■ 解答:
(1)
信号为偶函数,其中 sin 分量 =0。

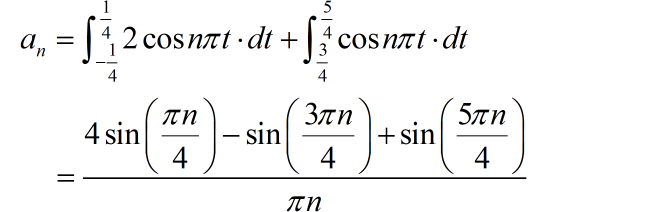
上面结果是使用了 sympy 进行了辅助计算。

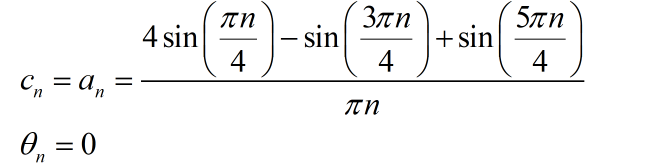
(2)
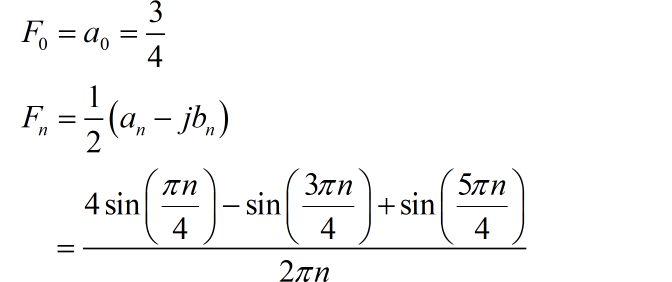
(3) 双边频谱
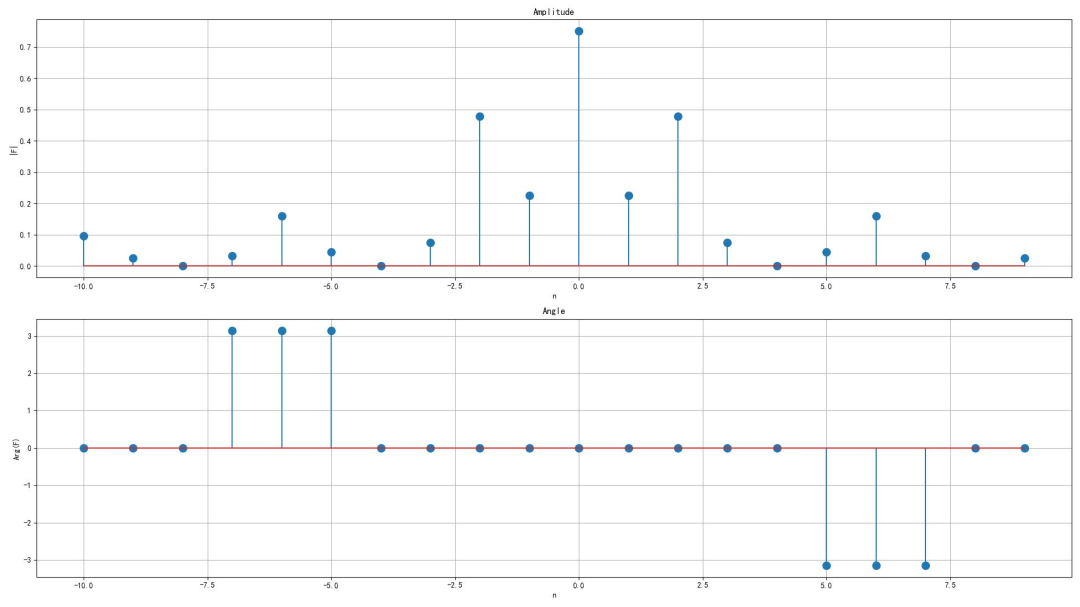
▲ 图1.1.4 信号的双边频谱(5)第五小题
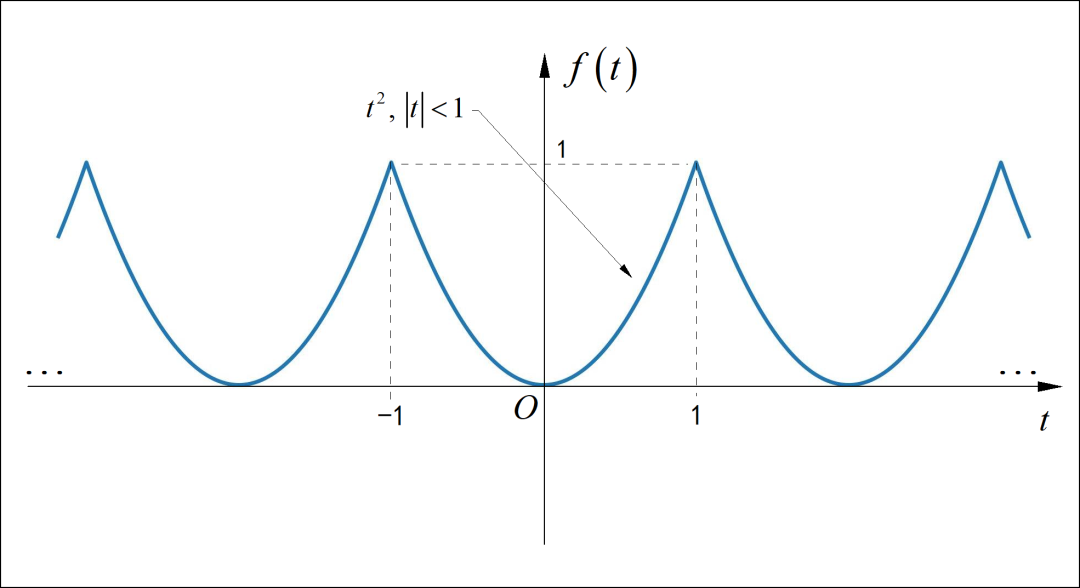
■ 解答:
(1) 信号为偶对称函数,所以 sin 分量 。
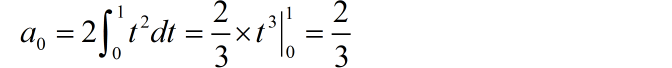
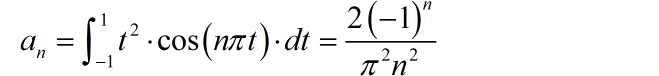
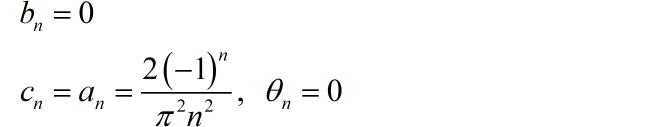
(2)
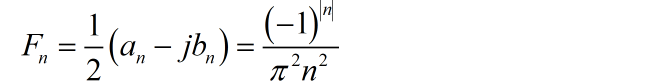
(3)
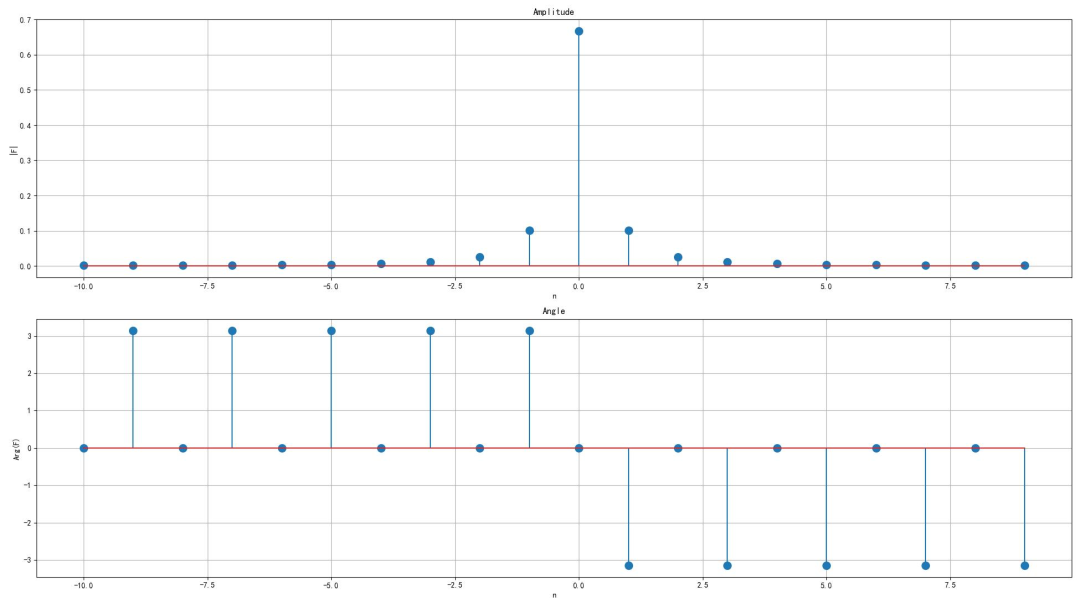
▲ 图1.1.5 信号的双边频谱
■ 解答:
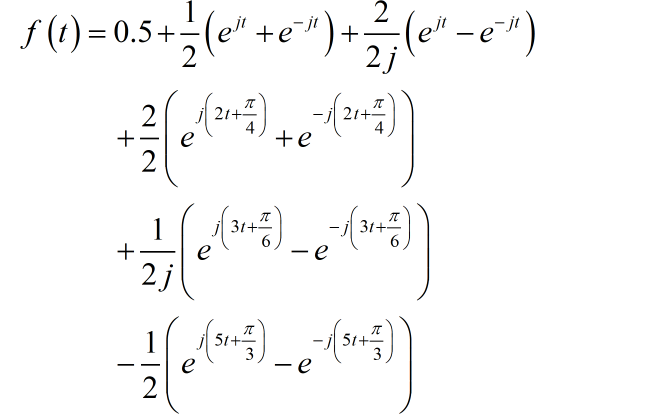

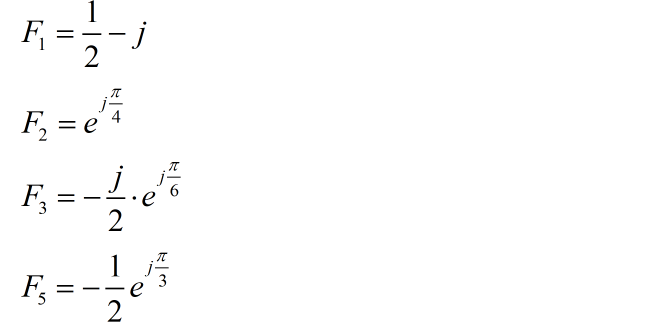
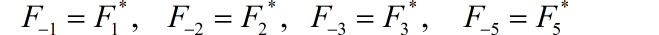
信号的双边频谱如下:
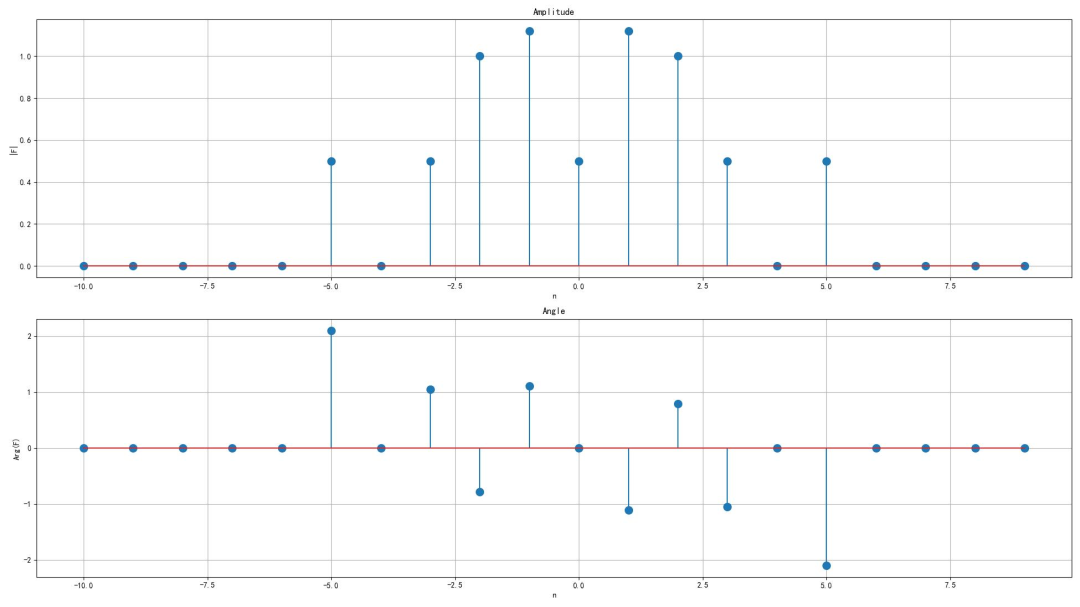
▲ 图1.1.6 信号的双边频谱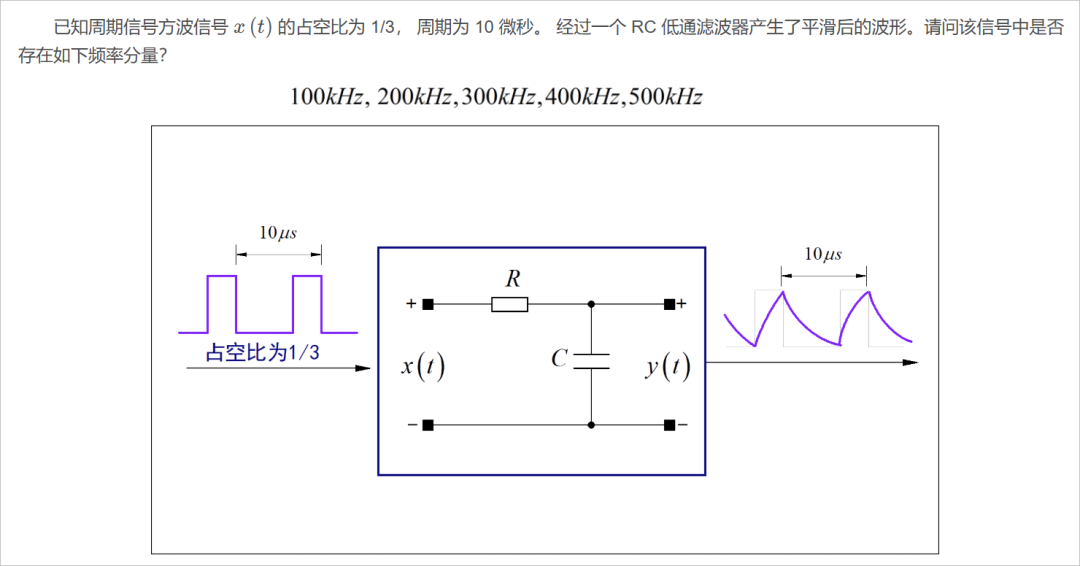
■ 解答:
信号的周期为 10微秒,对应的频谱为 100kHz。根据信号的占空比,可以知道它的谐波分量中不包含有三的倍数对应的谐波。信号经过RC低通滤波之后,信号的频谱分量不会发生变化。所以信号中不包含有 300kHz 的频率分量。
如果希望通过一个电路能够产生 300kHz 的频域分量,这个电路必须具有某种 非线性 或者 时变特性。可以使用一般的非线性放大电路 或者数字电路来实现。最简单的 一个方法,就是将上述滤波之后的信号输入到一个 比较器电路,调整比较器的阈值电压,使得它的输出对应的方波信号的占空比不再是 1/3 或者 2/3,那么信号中就会包括 300kHz 的频谱分量。
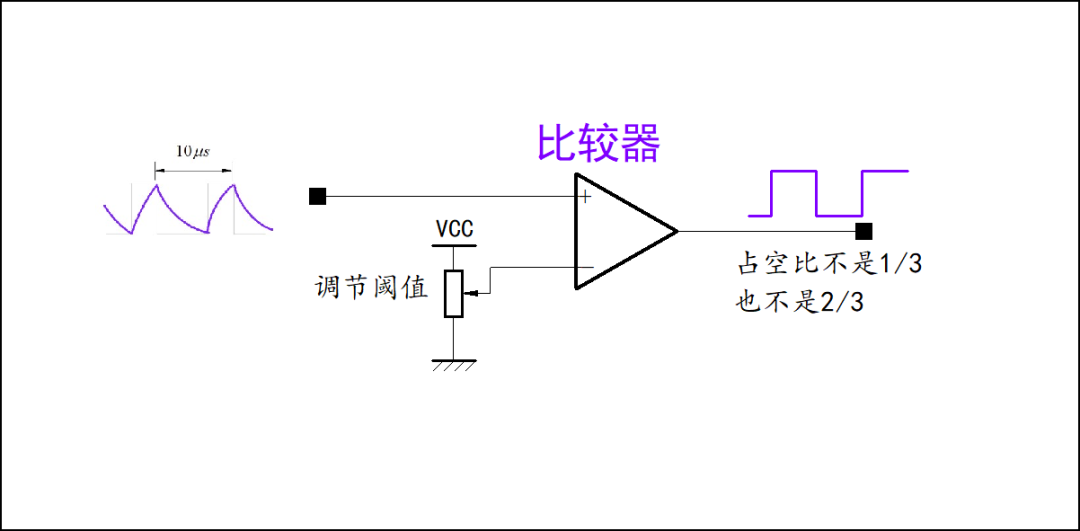
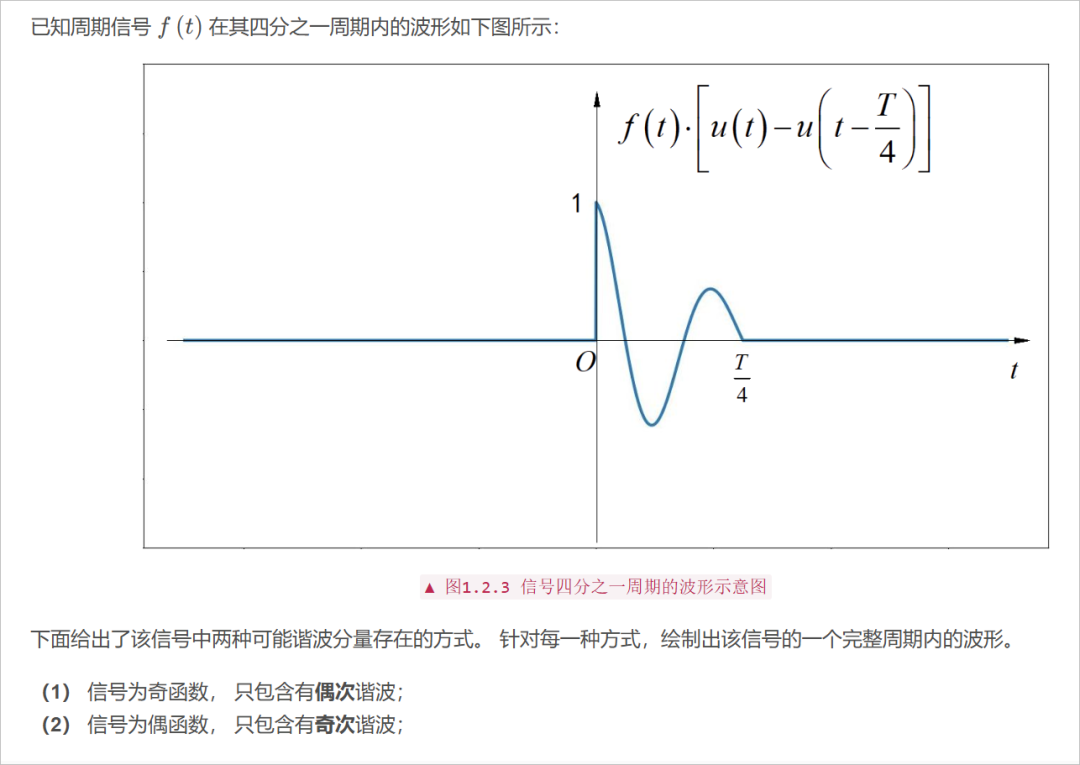
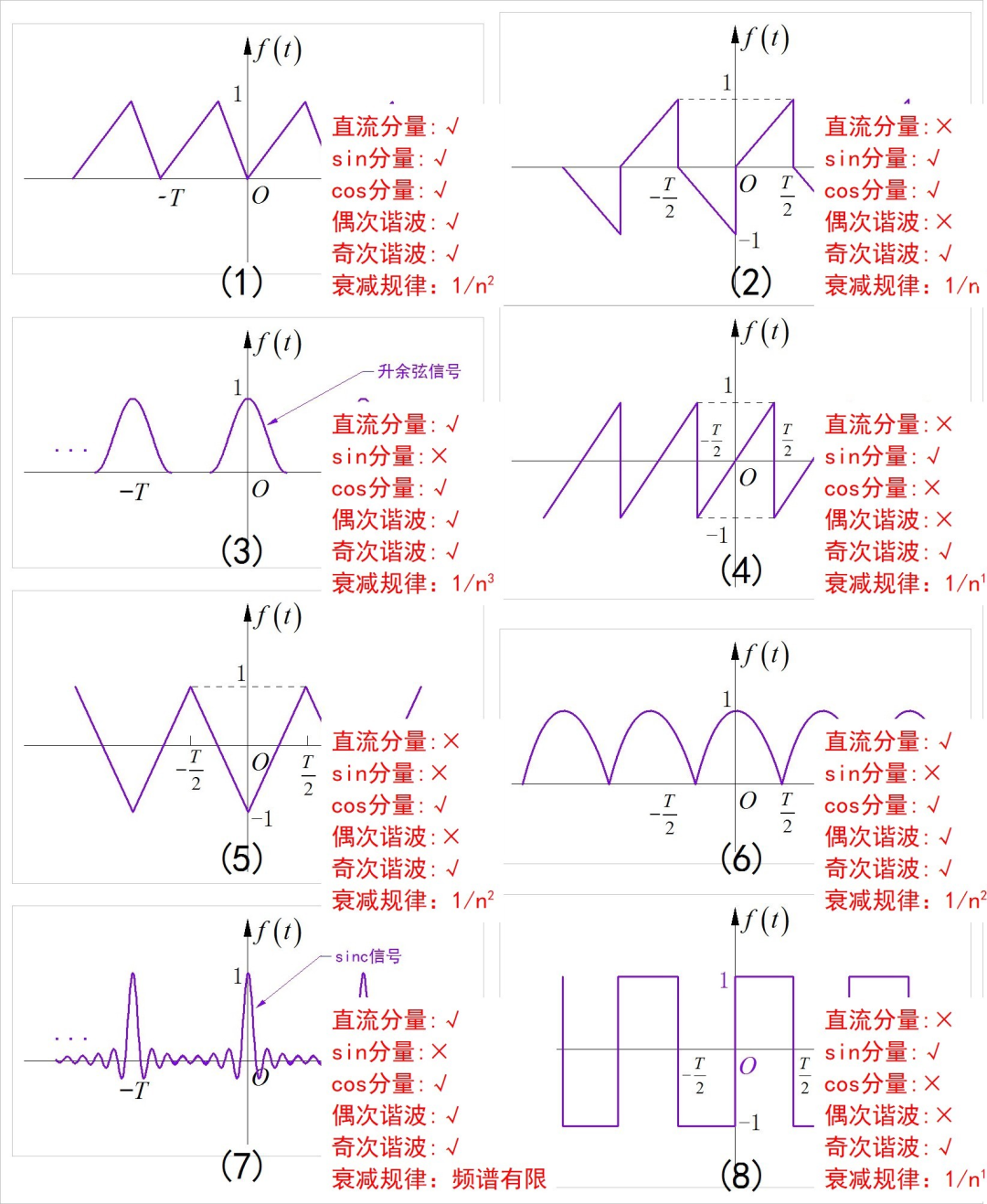
■ 解答:
(1) 信号为奇函数,只包含偶次谐波
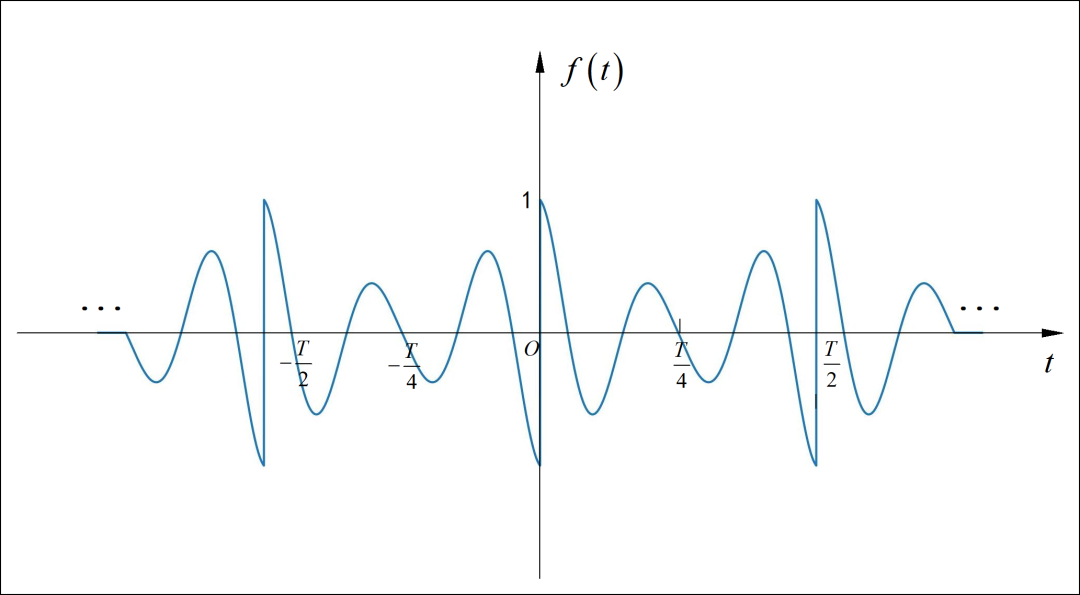
(2) 信号为偶函数,只包含奇次谐波
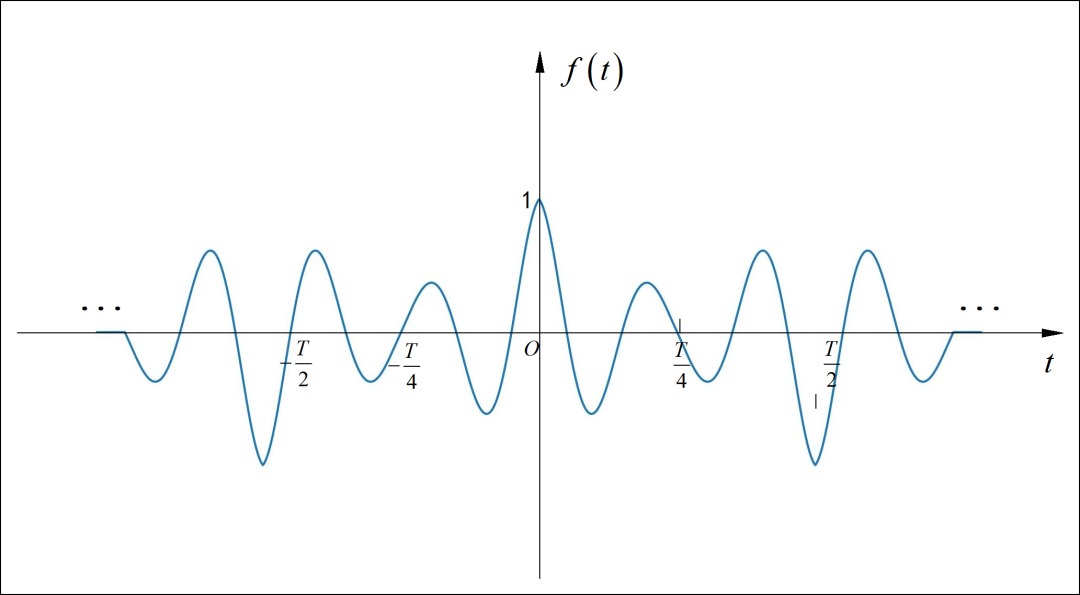
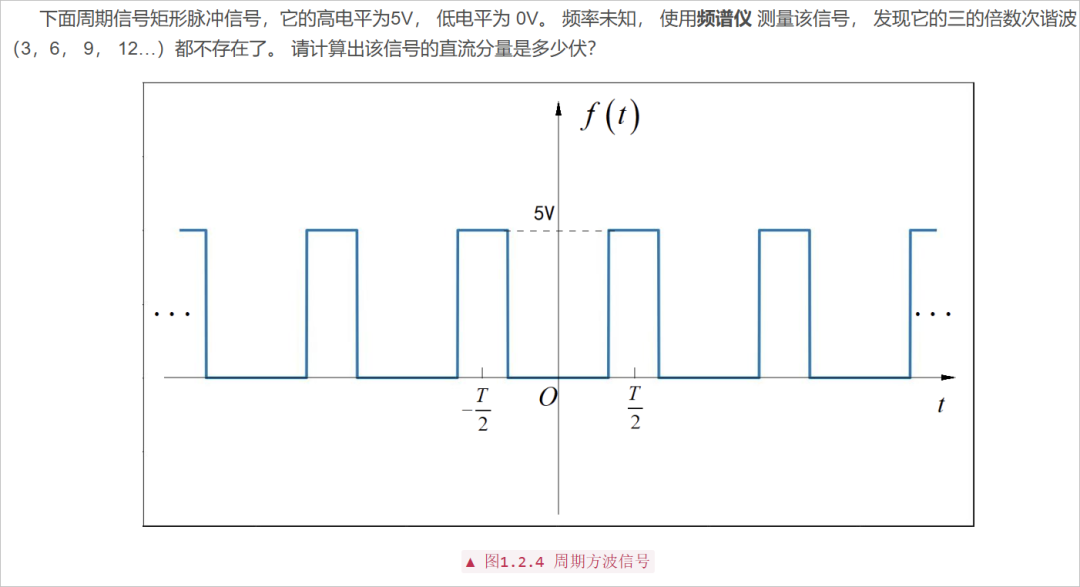
□ 解答:
对于周期矩形信号,它的傅里叶级数分解系数可以表述为:
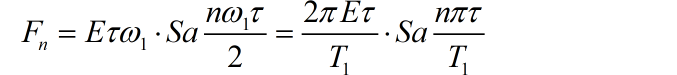
其中 分别是周期信号的 周期和高电平时间。可以看到,如果 或者 。则对应的 的取值为 0。因此,上述方波信号中,高电平在 一个周期内的比值可能为 1/3,或者 2/3。对应的直流分量就有可能为 5/3伏 或者 10/3 伏。
□ 解答:
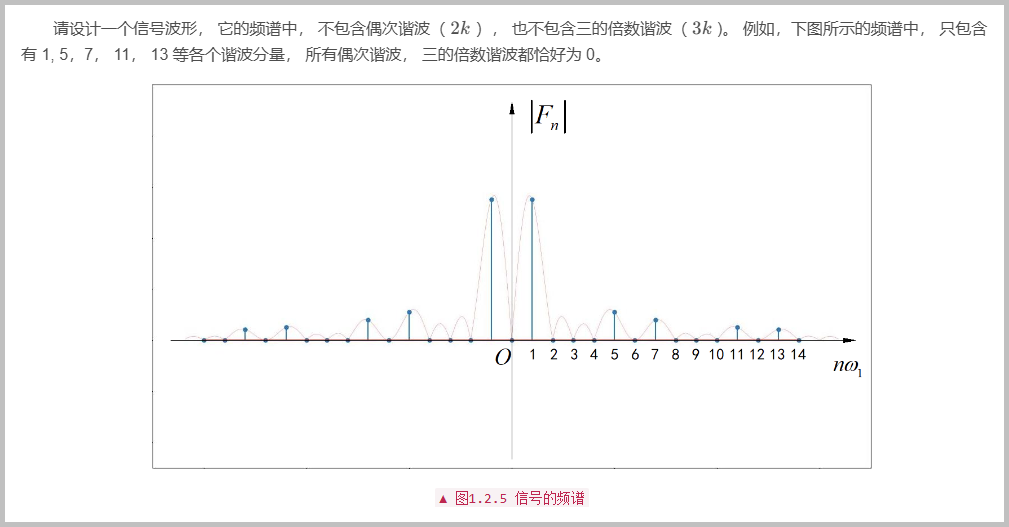
关于这个题目的分析,请参看博文: 消除信号中的谐波[4] 中的讲解。
■ 解答:

■ 解答: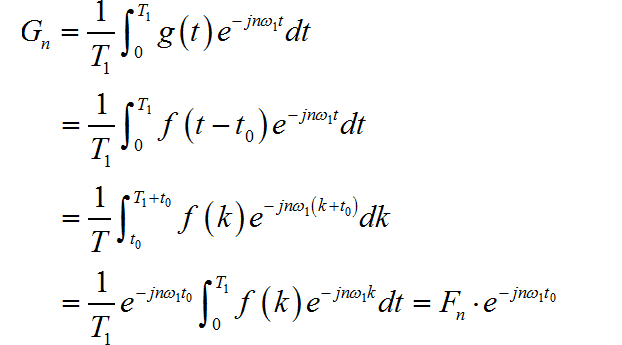
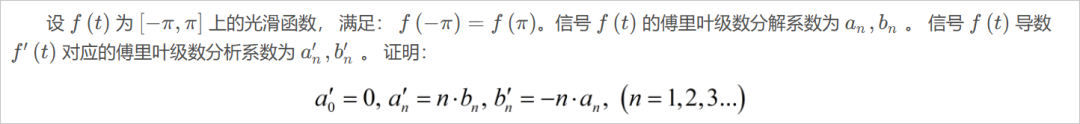
■ 解答:
根据题目可以知道周期信号的周期为 ,那么对应的傅里叶级数为:
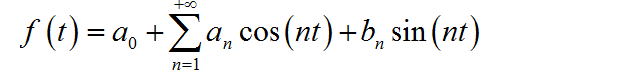
对上面等式两边进行求导:
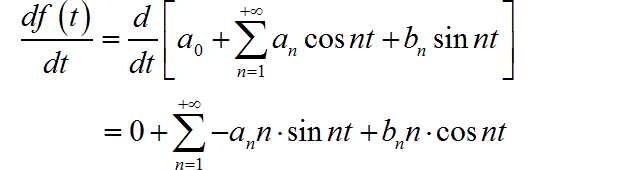
所以,对于 的傅里叶级数 与原来信号的傅里叶级数之间有如下关系:
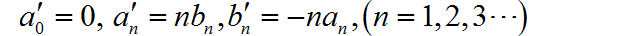

■ 解答:
根据条件 (1)(2)(3)(4)可以知道给定的函数值包含有一次谐波。根据条件(5)可以知道该谐波的功率为 1/2,所以该信号的有效值为 1/2 ,信号的峰值为 。
根据条件(6),可以知道该信号为 奇实 信号,所以信号的周期为 4,峰值为 的正弦信号。它的表达式为:

最终,信号参数为:
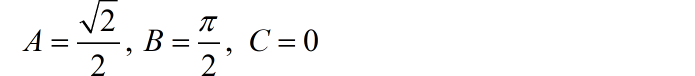
信号与系统2024(春季)作业要求以及参考答案汇总: https://zhuoqing.blog.csdn.net/article/details/136798840
[2]信号与系统2025(春季)作业要求及参考答案汇总: https://zhuoqing.blog.csdn.net/article/details/145879368?spm=1011.2415.3001.5331
[3]信号与系统分析2025(春季)作业要求:第五次作业: https://zhuoqing.blog.csdn.net/article/details/146358910?spm=1011.2415.3001.5331
[4]消除信号中的谐波: https://zhuoqing.blog.csdn.net/article/details/137173030