
下面信号中,如果包含有 ,那么它对应的傅里叶变换记作:

利用傅里叶变换的性质,求解下面信号的频谱。
(1)
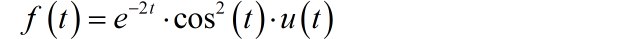
(2)
(3) 下图中有现长震荡信号的包络线为升余弦信号,震荡载波信号为 。
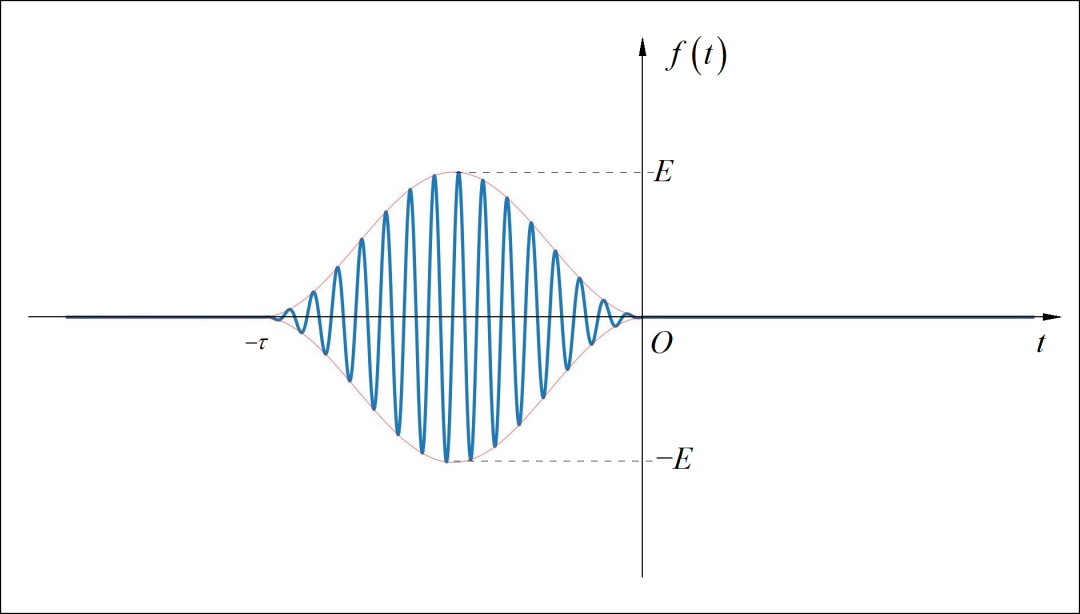
(4)
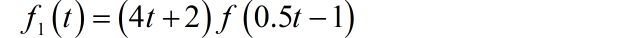
(5) 下图信号很像“升余弦”信号,但是它是两个等宽三角形信号的卷积。图中的三角形的参数已经给出,请写出卷积之后信号的频谱。
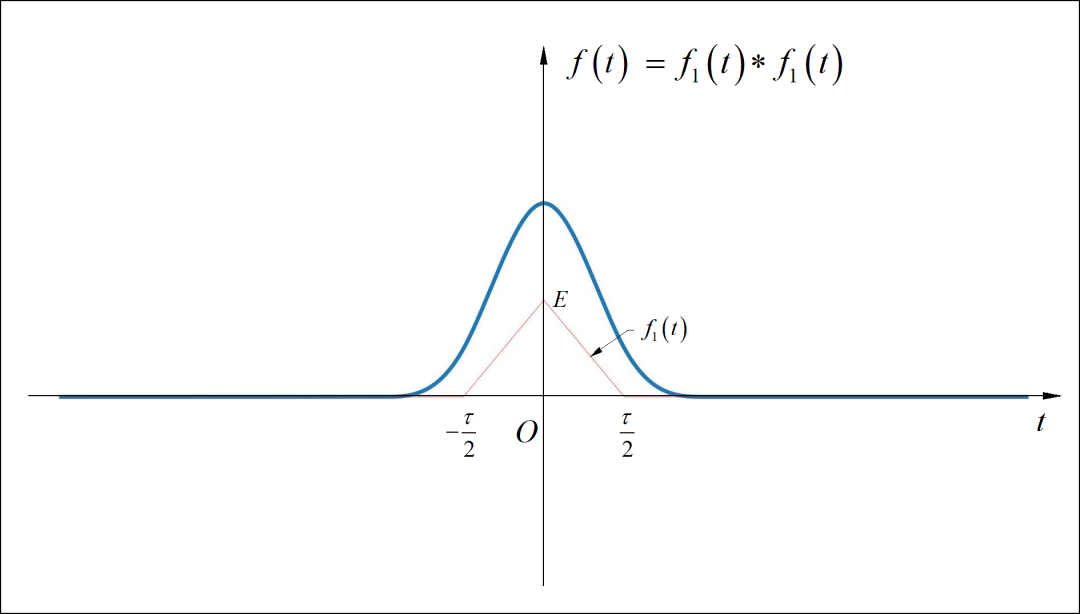
(6)
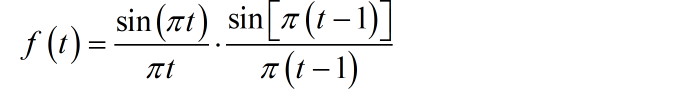
提示: 利用频域卷积定理;
(1)

(2)
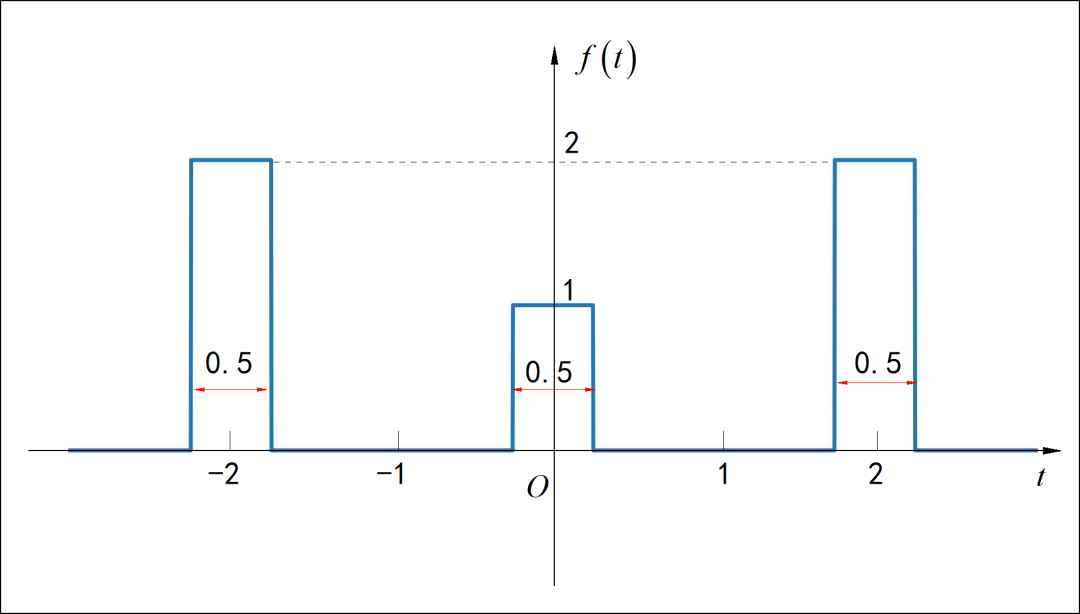
(1)
已知信号的频谱如下图所示,求信号 的表达式。
提示,利用对偶特性写出三角信号对应的时域信号,再应用频移特性求信号的表达式。
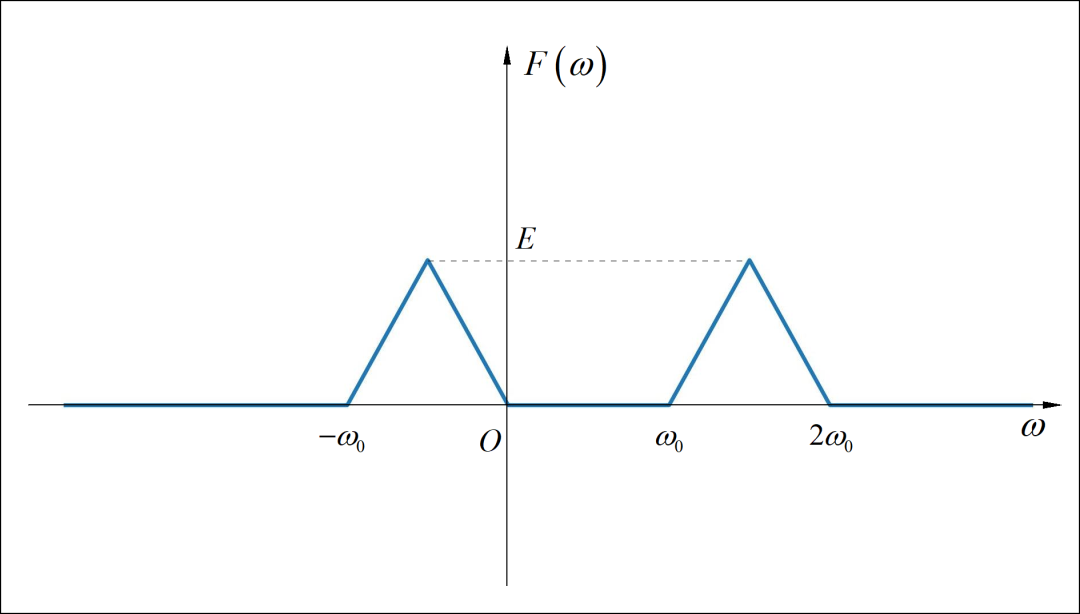
(2)

提示: 应用卷积性质。先写出 的傅里叶反变换,然后再应用卷积定理求 。
(3)

注意: 傅里叶反变换得到的信号应该满足 Diriclett 条件。
(1)
已知信号的频谱为:

求信号: 。

(2)
已知信号的频谱为:
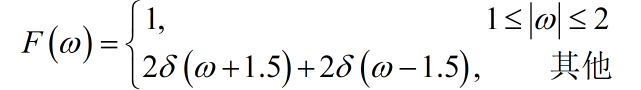
请绘制出 的频谱。
提示: 这个题目需要应用到FT 的频域卷积定义。 的频谱实际上是它自己的频谱与自己的频谱卷积。再考虑还有 的因子。
求下图所示周期号的傅里叶变化。
(1)
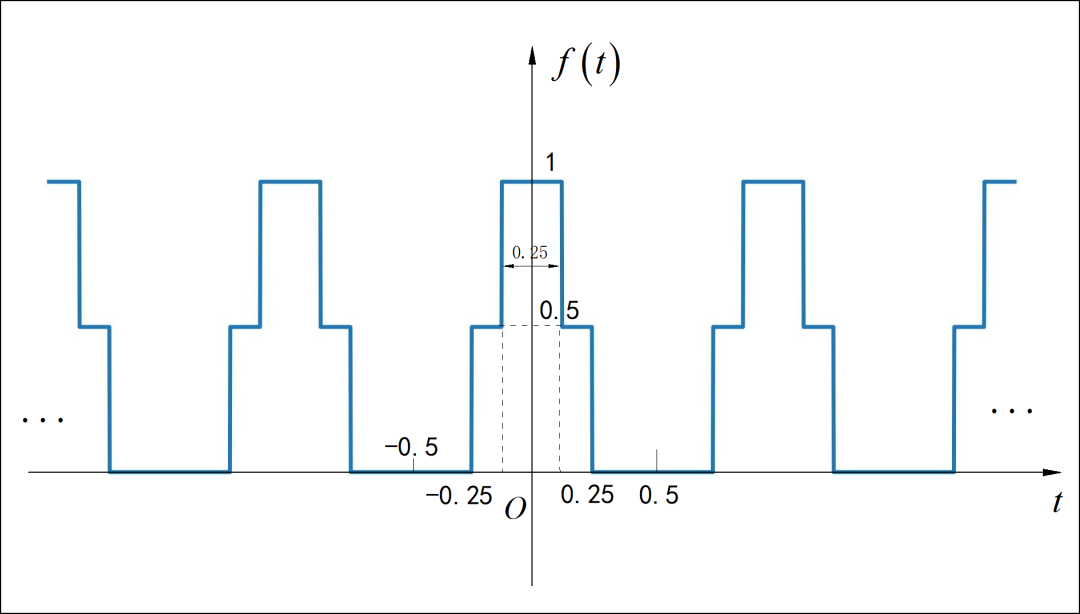
提示: 将单个周期信号的傅里叶变换进行“离散化”。
(2)
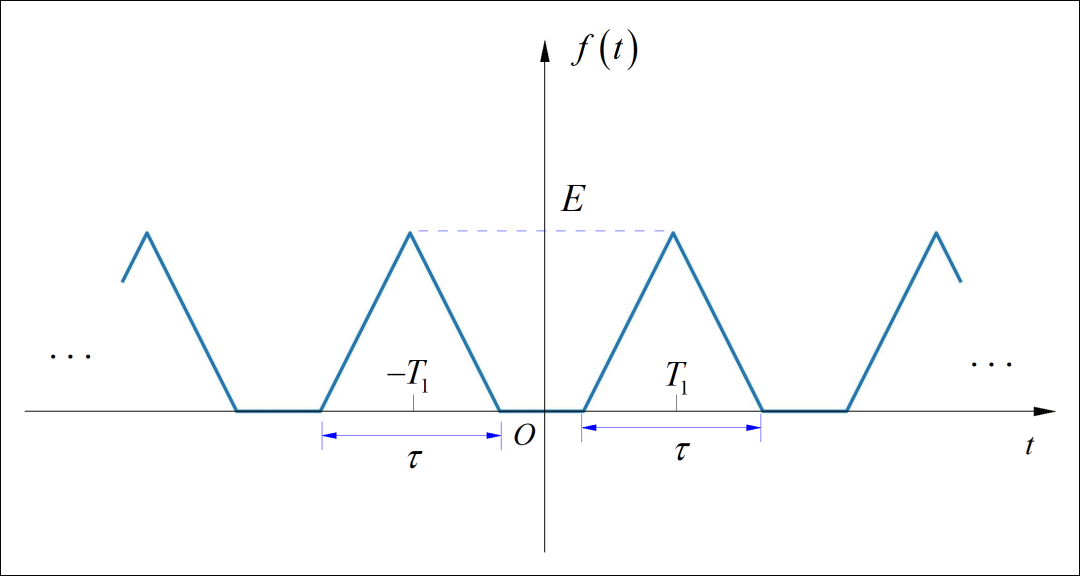
提示: 将单个周期信号的傅里叶变换进行“离散化”。
(1) 周期信号与三角波信号乘积
求下面信号的频谱。该信号是周期为 ,幅度为 ±1 的三角波信号,与宽度为 ,高度为 1 的对称三角脉冲信号相乘。
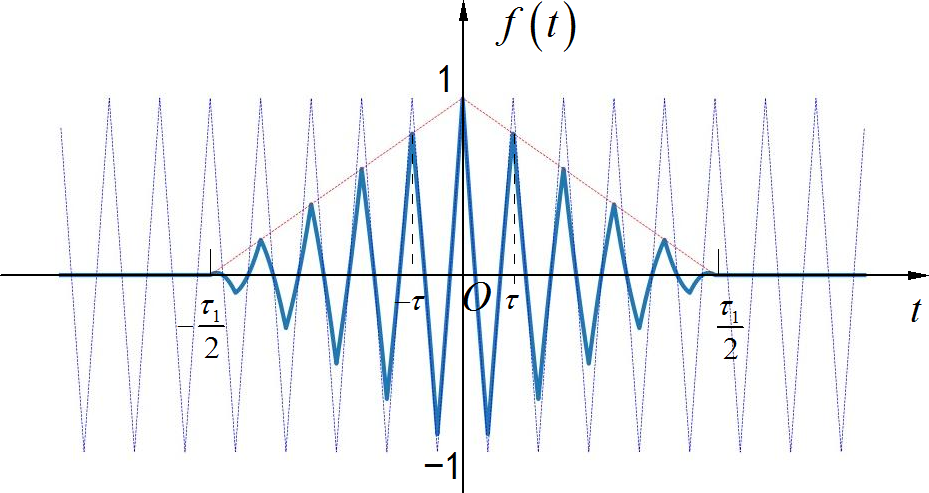
▲ 图1.2.2 调制在三角波上的三角波信号提示: 关于等腰三角形脉冲信号的频谱可以查询课件中给出的答案。使用傅里叶变换时域乘积对应频域卷积定理。
信号是由在 处不同采样数据 对应的折线构成。
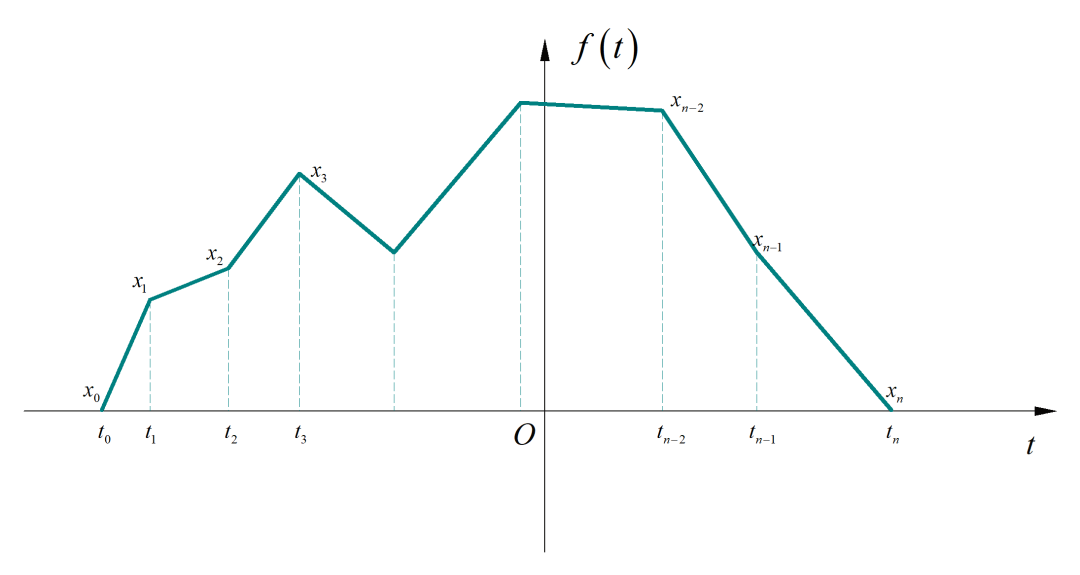
试证明该信号的频谱如下所示:

并使用 确定其中的 。
提示:使用傅里叶变换的微分定理。将折线信号微分两次,就形成在 处的冲激信号。冲激信号的强度,实际上是前后两个折线斜率的差值。利用已知的 ,可以写出每一个冲击信号的强度。下面的推导,就自行处理吧。
已知信号 的“希尔伯特变换” 的表达式为: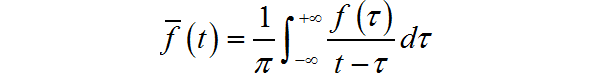
定义信号 的解析信号 为: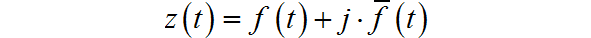
试证明:
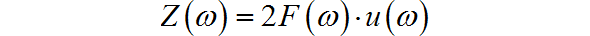
其中: 分别是 的傅里叶变换。 是关于 的单位阶跃函数。
信号的带宽 可以定义为包含信号能量 90% 的频带宽度,使用 表示,即:
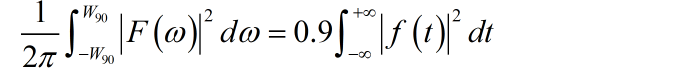
求信号 ( ) 对应的 。
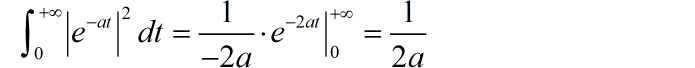
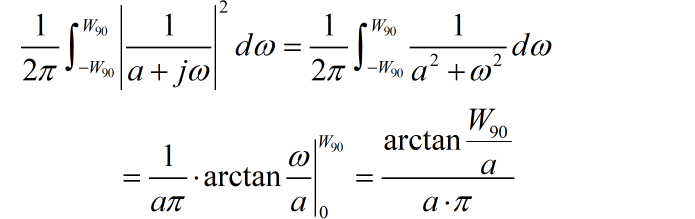
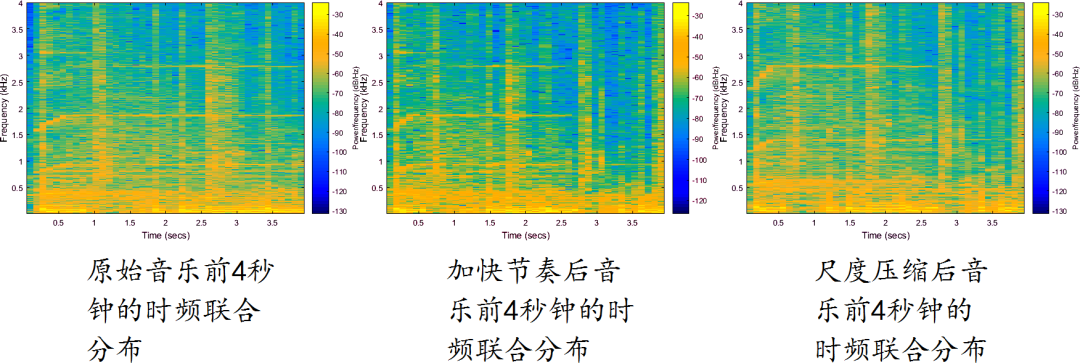
在网络学堂下载一段音乐及其经过处理后的音乐数据文件,聆听相应的音频效果。
使用MATLAB中使用spectrogram 命令观察音乐及其变换后的数据是时频联合分布,总结节奏变化一是尺度变化两种操作在听觉和信号时频联合分布之间的差别。
音乐数据文件与作业要求文档合并在一起,HMW7-DATA.ZIP文件。
信号与系统2024(春季)作业要求以及参考答案汇总: https://zhuoqing.blog.csdn.net/article/details/136798840
[2]信号与系统 2023年春季学期期末考试命题: https://zhuoqing.blog.csdn.net/article/details/131068697
[3]信号与系统期末2024年春季学期期末考试命题-模拟考试: https://zhuoqing.blog.csdn.net/article/details/139587106
[4]信号与系统期末2024年春季学期期末考试命题-正式考试试题: https://blog.csdn.net/zhuoqingjoking97298/article/details/139640739?csdn_share_tail=%7B%22type%22%3A%22blog%22%2C%22rType%22%3A%22article%22%2C%22rId%22%3A%22139640739%22%2C%22source%22%3A%22zhuoqingjoking97298%22%7D
[5]信号与系统2025(春季)作业要求及参考答案汇总: https://zhuoqing.blog.csdn.net/article/details/145879368