光学史上的那些人儿--- 马吕斯
第十九章 马吕斯光学
《马吕斯光学》
方解石前悟偏振,余弦定律映苍穹。
冰洲石裂双光影,, 波粒之争起微芒。
1 马吕斯与光的故事
1801年,马吕斯随拿破仑的远征军返回巴黎。在埃及的沙漠中,他曾无数次观察到阳光在尼罗河面反射的刺目光芒,那些光线仿佛带着某种神秘的秩序。回到巴黎后,他开始在巴黎工艺学院的实验室里反复实验,试图解开光的奥秘。
时值 1808 年,深秋的寒意侵蚀着厚厚的丝绒窗帘的边缘。闪烁的煤气灯在埃蒂安-路易·马吕斯的杂乱的巴黎书房里投下长长的、跳动的阴影。马吕斯是一位习惯严谨,在科学界声誉鹊起的人,他正沉浸在他的工作中,一些方解石晶体在昏暗的光线下闪闪发光。

马吕斯并非专职科学家,却在拿破仑远征埃及的炮火中与光学结缘。作为随军工程师,他曾用望远镜测绘尼罗河三角洲,却总被镜片中扭曲的光斑困扰。归国后,他将实验室设在巴黎天文台的阁楼,用棱镜、透镜和自制的偏光装置反复验证一个猜想:光的振动或许存在方向性。
几个星期以来,马吕斯一直在细致地研究双折射现象,即光线在穿过这些晶体结构时分裂成两束光线的奇特方式。他坚信牛顿的光微粒说,将光设想为一束微小的粒子。 他认为,可以通过仔细的观察和数学分析来解释这些奇怪的光学现象,所有这些都在牛顿既定的原则框架内。
一天下午,在工作到很晚的时候,马吕斯决定转移他的注意力。 他没有检查穿过晶体的光,而是将注意力转向反射回房间对面窗户的光。 午后迟到的阳光,透过巴黎的薄雾,在窗格上投射出朦胧的光芒。 他拿起一块方解石晶体,这是他在几周的实验中养成的一个习惯。 他打算用它来分析反射光的特性。
当他转动晶体时,一些非同寻常的东西引起了他的注意。 通过方解石观察到的反射光的强度随着每一次转动而发生剧烈的变化。 仿佛这束光获得了一种“偏向性”,一种他以前在普通光中没有观察到的奇特特性。 他花了几个小时一丝不苟地重复这个实验,仔细地改变了窗户的角度和方解石的方向。 结果始终相同。
马吕斯对此很感兴趣,于是放弃了对方解石双折射的研究,全身心地投入到这个新现象中。 他用不同的反射面——玻璃、水、抛光金属——进行了实验,发现当光线以特定的角度照射到表面时,效果最为明显。 他意识到反射光线的表现就好像它被“过滤”了一样,优先在某个方向上对齐。
马吕斯是数学精度的专家,他开始对他的观察结果进行量化。 他一丝不苟地测量了当他转动方解石晶体时通过它的光的强度,并仔细地绘制了数据。 他发现了一个一致的数学关系:强度随着晶体轴与和反射光相关的特定方向之间的角度的余弦的平方而变化。 他将此称为“偏振”,这是他创造的一个术语,用来描述光线这种新的“偏向”特性。 他制定了后来被称为马吕斯定律的公式,这是一个描述这种关系的精确方程。
他在科学院宣读论文,提出著名的马吕斯定律:偏振光的强度随偏振片角度的余弦平方变化。
1809年春,马吕斯在实验中记录了大量数据。他发现,当偏振光通过分析器时,透射光的强度与两晶体夹角的余弦平方成正比。这一规律后来被命名为马吕斯定律。然而,他的健康却因长期熬夜每况愈下,肺结核的阴影始终笼罩着他。
某日,同事毕奥来访,两人在实验室争论不休。毕奥认为光的偏振应由波动理论解释,而马吕斯尚未完全接受。尽管观点不同,他们仍合作研究折射光的偏振现象,并共同提出确定晶体光轴方向的方法。毕奥的波动说观点最终让马吕斯深受启发,他意识到自己的发现与惠更斯的波动理论或许能完美契合。
即使对马吕斯本人来说,这个发现也是革命性的。 以这种方式运作的光粒子的概念很难与牛顿的微粒说相协调。 他被迫面对越来越多的支持光波动理论的证据,这些理论是由托马斯·杨等人倡导的。
1811年,年轻的菲涅耳带着波动说的数学模型闯入光学界。他用横波理论解释了马吕斯的偏振现象,甚至推导出著名的菲涅耳公式,精确计算了反射光和折射光的振幅比。马吕斯起初对菲涅耳的数学推导感到陌生,但当他看到公式完美预测实验结果时,不禁感叹:“这正是我寻找的理论!”
两人虽年龄相差17岁,却成为挚友。菲涅耳将马吕斯的实验数据融入波动说,最终证明光是一种横波;而马吕斯则为菲涅耳的理论提供了关键的实验证据。他们的合作让光学研究从现象描述迈向了理论统一。
1812年2月,马吕斯的咳嗽愈发严重。他躺在病榻上,仍在修改关于双折射的论文。窗外的巴黎下着细雨,他想起在埃及沙漠中观察到的光,想起冰洲石折射的两道光束——它们如同科学的两条路径:实验与理论,缺一不可。
临终前,他握着毕奥的手说:“告诉菲涅耳,光的偏振……是自然的诗篇……”数小时后,这位36岁的科学家与世长辞。他的发现成为菲涅耳波动说的基石,而马吕斯定律至今仍在光学课堂上被反复提及。
他留下的不仅是定律与公式,更是一种科学精神:用数学语言诠释实验现象,以理性之光突破经验桎梏。他的偏振理论为菲涅耳的横波模型奠定基础,最终促使麦克斯韦将光纳入电磁理论框架。现代光学仪器、3D 电影、液晶显示等技术,皆源于他对光的 “方向性” 的执着追问。
在巴黎先贤祠的穹顶下,马吕斯的名字与其他科学巨匠并列。他的故事提醒世人:科学的突破往往始于偶然的观察,却需要研究者以数学为舟,在现象与理论的海洋中执着航行。
2 马吕斯的光学理论
马吕斯以发现光的反射偏振而闻名。虽然他没有像牛顿或杨氏那样发展出全面的“光学理论”,但他对偏振的研究极大地促进了对光的理解,并为后来电磁理论的发展奠定了基础。1809年,他发表了一篇关于通过反射发现光的偏振的论文,1810年发表了一篇关于晶体中光的双折射(弯曲)理论的回忆录。
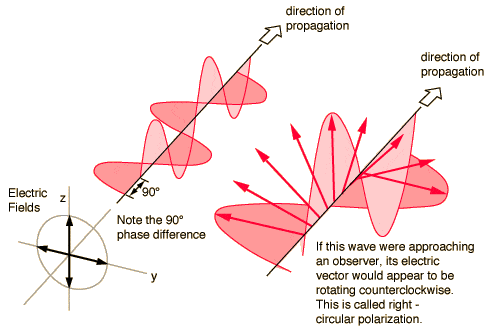
2.1 光的偏振
在研究双折射现象的过程中,马吕斯偶然通过方解石晶体观察了卢森堡宫窗户反射的阳光。令他惊讶的是,当他绕视线轴旋转晶体时,两个影像的强度会发生变化。他推测,反射光线获得了一种不对称性,类似于惠更斯观察到的方解石晶体发出的寻常光与非寻常光的特性。他很快发现,当反射发生在特定入射角时(例如水面的入射角为 52°45'),这种类比完全成立。例如,只有当反射光进入主截面(即垂直于晶体表面且平行于光轴的平面)与反射面平行的晶体时,才会发生寻常折射。马吕斯于 1808 年 12 月 12 日在法国科学院公布了这些研究结果。
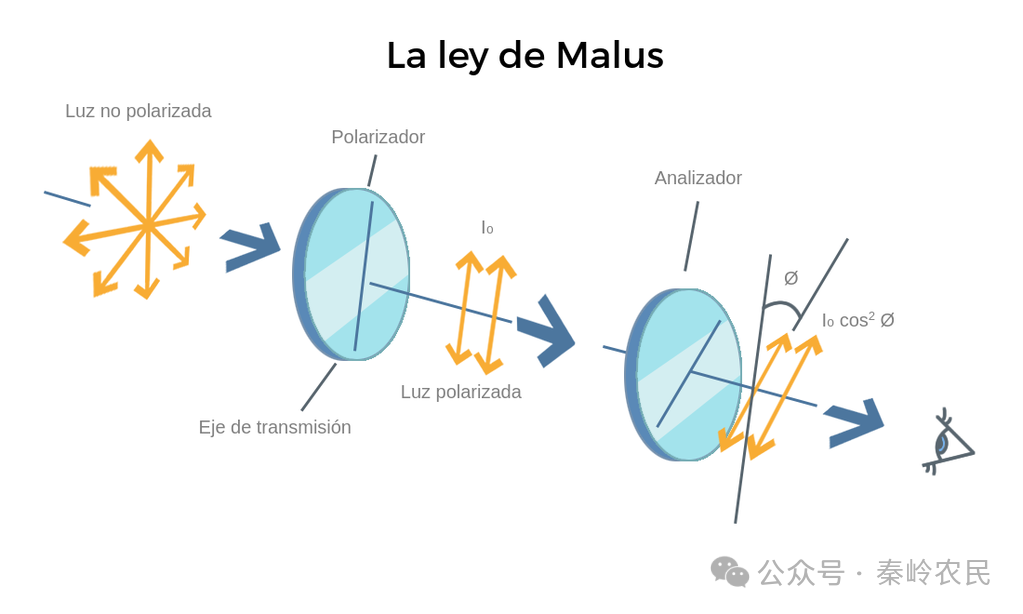
三个月后,马吕斯报告称,当两块玻璃板的反射面呈正交状态时,以偏振入射角(54°35′)反射的玻璃板所反射的光,在以相同入射角照射第二块玻璃板时将不再发生反射。马吕斯补充道,若两块玻璃板的反射面形成的夹角为θ(在其他条件相同的情况下),反射光的强度将随cos²θ变化。由于缺乏精确的光度测量手段,马吕斯可能选择这一规律(即余弦平方定律),是因为它是最简单的三角函数公式,能够正确计算出光强最小值和最大值对应的夹角。这就是马吕斯定律
I = I₀ cos²θ
I是透射光的强度,I₀ 为入射光强度,θ为入射光的偏振方向与偏振器透射轴之间的夹角。
在马吕斯看来,他后来称为“反射偏振”的这一发现决定了光的本质:
All the ordinary phenomena of optics can be explained either by Huygens’s hypothesis, which traces them to the vibrations of an ethereal fluid, or according to Newton’s opinion, which traces them to the action of bodies on the luminous molecules considered as belonging to a substance subjected to the attractive and repulsive forces that serve to explain the other phenomena of physics. The laws concerning the progress of rays in double refraction can still be explained by either hypothesis. In contrast, as the above given observations prove that the phenomena of reflection differ for the same angle of incidence—which cannot happen under Huygens’s hypothesis, the author concludes not only that light is a substance subjected to the forces that animate other bodies but also that the form and disposition of these molecules have a great influence on the phenomena.
所有普通光学现象既可以用惠更斯的假说解释(将其归因于以太流体的振动),也可以依据牛顿的观点解释(将其归因于物体对光微粒的作用 —— 这些微粒被视为受吸引与排斥力支配的物质,而这些力同样用于解释其他物理现象)。关于双折射中光线传播的定律仍可由两种假说共同解释。然而,正如上述观察结果所证明的:相同入射角下的反射现象存在差异(这在惠更斯假说下不可能发生),作者由此得出结论:光不仅是一种受支配其他物体之力作用的物质,且这些微粒的形态与排列对现象具有重大影响。
马吕斯像牛顿一样假设光微粒具有横向不对称性,并用分子轴 a、b、c 描述这一特性。他进一步假设,横向轴 b 和 c 的取向取决于物质施加的排斥力方向:
If we consider, in the translation of luminous molecules, their movement around three principal axes a, b, c, the quantity of molecules whose b or c axis becomes perpendicular to the direction of the repulsive forces is always proportional to the square of the sine of the angle that these lines need to describe in their rotation around the axis a in order to assume this direction, and, reciprocally, the quantity of molecules whose b or c axes become the closest possible to the direction of the repulsive forces, is proportional to the square of the cosine of the angle that these lines need to describe in their rotation around the axis a in order to be included in the plane which contains this axis and the direction of the forces.
若我们考虑发光微粒(luminous molecules)围绕三个主轴a、b、c的运动,则当微粒的b轴或c轴与排斥力方向垂直时,其数量始终与该角度的正弦平方成比例——该角度是这些轴围绕a轴旋转时,需达到的方向调整角度。反之,当微粒的b轴或c轴尽可能接近排斥力方向时,其数量与该角度的余弦平方成比例——该角度同样是这些轴围绕a轴旋转时,需达到的方向调整角度,且此时,轴需包含在由a轴和排斥力方向所确定的平面内。
从这一略显神秘的分子原理出发,马吕斯试图推导出一套关于任意介质对和任意入射角下的部分反射与折射的完整理论。部分反射曾是新牛顿学派光理论家的难题,他们对牛顿的假设(如“易与难的倾向”)持保留态度。
马吕斯将偏振现象视为这一现象的关键,他认为自然光是所有方向偏振光的混合。在 1810 年发表的《关于双折射的回忆录》中,系统分析了晶体(如方解石)对光的双折射现象。他发现:寻常光(o 光)和非寻常光(e 光)具有不同的偏振方向。晶体的光学性质与其微观结构(如分子排列)相关,为后续晶体光学研究奠定基础。他在1811年宣读的最后几篇论文中,记录了不同入射光偏振方向下反射光强度与透射光偏振状态的观测数据。
马吕斯的这一数学模型试图用牛顿的粒子说解释偏振现象,但其“正弦平方”与“余弦平方”的关系实际上与惠更斯-菲涅耳的波动理论(如马吕斯定律)殊途同归。尽管他坚持光的微粒本质,但通过引入“主轴”和“排斥力方向”的动态关系,间接描述了振动方向的定向性,为后续横波理论提供了重要过渡。这一尝试也体现了科学理论从粒子说到波动说的复杂演进过程。
马吕斯的发现开辟了光学研究的全新领域。关于偏振的基本实验易于复现,并且可以进一步改进。尽管马吕斯未能找到偏振角i与折射率之间的规律性关系,苏格兰实验家大卫·布儒斯特(David Brewster)却发现了定律
Tan(iB)=n
这一公式因此以他的名字命名(布儒斯特定律)。正如后文将看到的,他在折射偏振、金属反射偏振以及晶体偏振角方面的大量精确实验,成为法国光学界领袖的重要研究资源。
虽然他的生命短暂,但对光学领域做出了持久的贡献,这些贡献今天仍然相关。
马吕斯通过反射发现了偏振现象,这是理解光的本质及其与物质相互作用的关键一步。他的工作为光波的横向性质提供了强有力的证据。马吕斯定律成为光学的基本定律,用于计算偏振光的强度。他对偏振和双折射的研究为后来电磁理论的进步和偏振光显微镜和其他光学技术的发展铺平了道路。
他的名字被“马吕斯定律”和月球上的马吕斯陨石坑所纪念。
附19 马吕斯简介

埃蒂安-路易·马吕斯(Étienne-Louis Malus,1775年7月23日-1812年2月24日),法国物理学家、数学家和工程师。 他最著名的成就是发现了光的偏振现象,特别是通过反射产生的偏振,并因此而闻名于世。 马吕斯的工作对光学领域的发展做出了重要贡献。
马吕斯于1775年出生于法国巴黎的一个富有家庭。 他的父亲是一位皇家财务官员,并对数学颇有造诣,因此马吕斯从小就受到了良好的教育和数学启蒙。
他在早年表现出对数学和科学的浓厚兴趣。 1796年毕业于巴黎综合理工学院(École Polytechnique),后进入梅济耶尔军事工程学院学习,接受了严格的数学和科学训练。马吕斯毕业后成为一名军事工程师,并在法国军队中服役。
1798—1801 他参加了拿破仑的埃及远征,期间他继续进行科学研究。在繁忙的军事生涯中,马吕斯仍然坚持进行科学研究。 他对光学,特别是光的偏振现象表现出了浓厚的兴趣。
1807年,他开始研究双折射现象,支持了惠更斯的波动理论。
1809 年发现光通过玻璃反射时产生偏振,提出 “马吕斯定律”,解释了偏振光强度与角度的关系。
1810年发表关于晶体双折射的理论,推动了几何光学的发展。同年当选巴黎科学院院士。
1811年,他与让-毕奥(Jean-Baptiste Biot)独立发现折射时光的偏振现象,并提出确定晶体光轴的方法。
1812年获伦敦皇家学会奖章。
1812年2月24日因病去世,年仅36岁,
埃蒂安-路易·马吕斯是一位才华横溢的科学家,他在短暂的一生中对光学领域做出了重要贡献。 他发现的光的偏振现象和提出的马吕斯定律成为光学领域的重要基础知识。