

■ 解答:
(1) 系统的完全解
使用经典三部曲方法求解系统的完全解。
微分方程的对应的齐次方程的特征方程为:
方程有两个单根: 。因此,方程的齐次解为:

根据输入信号的形式,它是一个指数信号,并与齐次解中的两个指数信号不同,所以,对应特接的一般表达式为:
带入原方程右边,进行化简,并求特接中的待定系数:
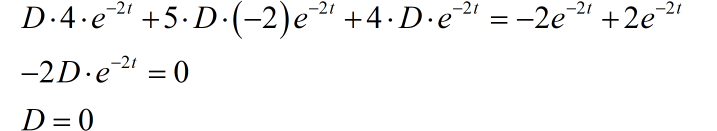
所以特解为 0。可以得到系统的完全解为:

使用奇异函数匹配方法,确定 。根据方程右边的表达式以及输入信号的形式,确定方程右边在 之间的奇异函数为:
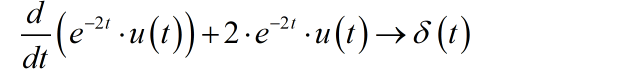
因此,方程右边最高导数项 的奇异函数以及各界导数的一般表达式为:
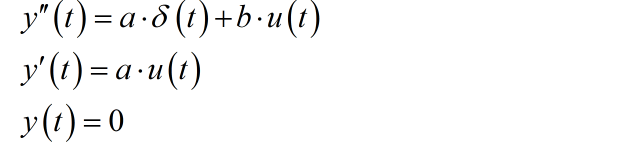
带入方程的,进行化简: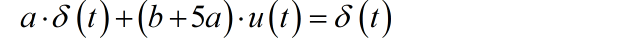
根据方程左右奇异函数同项系数平衡,可以得到 . 所以:
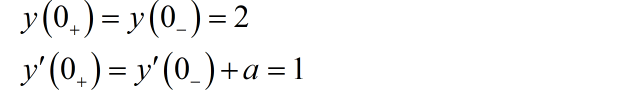
利用得到的初始条件 ,代入完全解,可以得到:
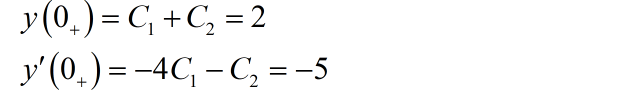
可以求得 。系统的完全解为:
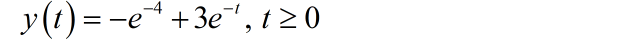
可以使用Laplace变换求系统的完全解,对应的程序如下。
(2) 完全解中的自由响应、强迫响应、瞬态响应、稳态响应如下:
根据完全解以及 ,可以求取系统的零输入响应:
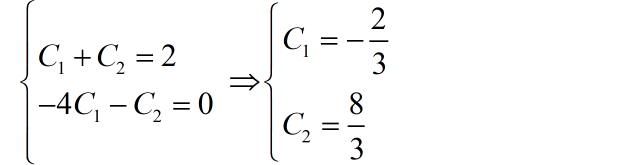
因此,系统的零输入响应为:
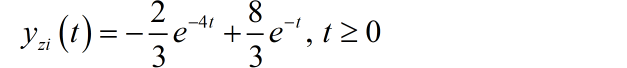
系统的零状态响应为: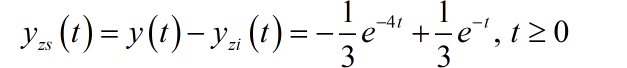
(3)
□ 求系统的单位冲激响应
下面求系统的单位冲激响应。根据前面求取完全解的过程,可以知道对于系统的完全解就是它对应的齐次解。根据奇异函数匹配方法,确定系统的初始条件 。在输入为单位冲激函数的时候,微分方程右边奇异函数最高导数项为 ,因此,方程左边各阶导数的奇异函数的一般形式为:
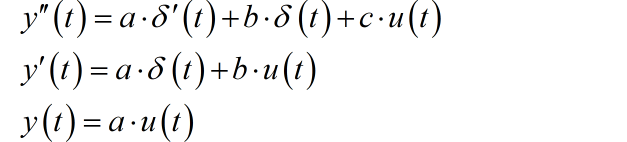
带入微分方程左边,化简之后为:
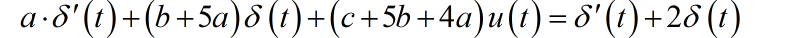
对比方程左右两边的奇异函数系数,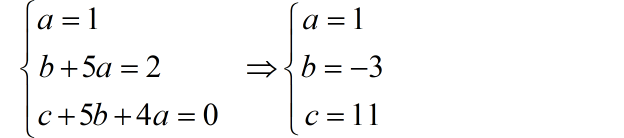
由此,可以得到系统的初始条件:
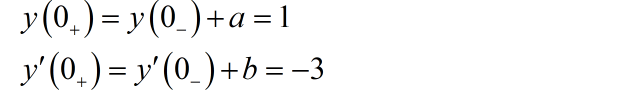
将上述初始条件,代入完全解
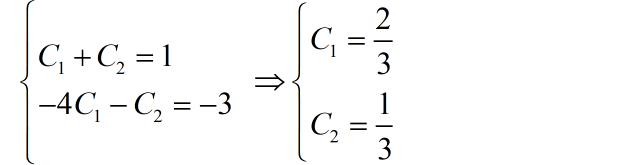
因此,系统的单位冲激响应为:
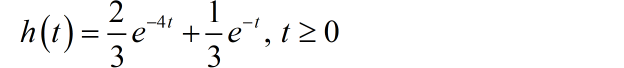
□ 求系统的单位阶跃响应
微分方程的齐次解与前面求解单位冲激响应对应的齐次解是相通的。由于输入信号为 ,所以有对应的特解常量,设为 。带入方程左右: ,可以得到对应的特解 。由此,微分方程的完全解为:
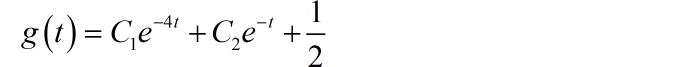
根据奇异函数匹配方法,求系统的初始条件: 。将 代入方程的右边,得到奇异函数最高导数项为 ,所以,方程左边输出信号各阶导数的奇异函数一般形式为:
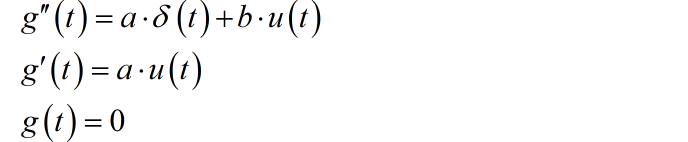
代入方程,化简可得: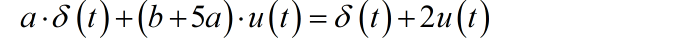
对比方程左右奇异函数系数,可得:

因此,系统的初始条件为:
代入完全解
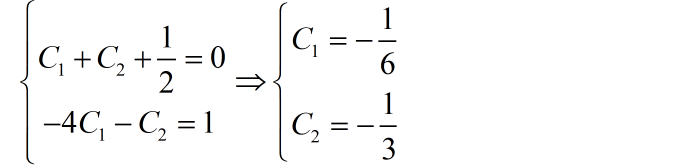
因此,系统的单位阶跃响应为
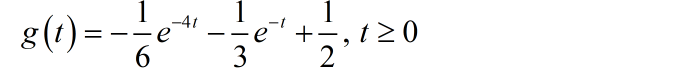
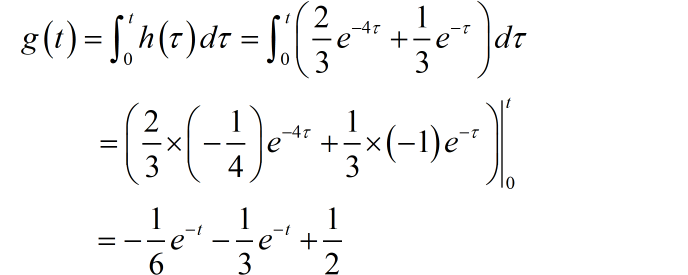

■ 解答:
(1) 使用经典的三部曲方法求差分方程的解。
根据方程的齐次方程形式,得到对应的特征方程, ,得到两个特征根: 。方程的齐次解为:
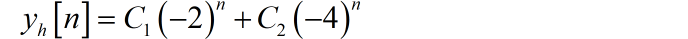
根据输入信号,可以知道方程的特解形式为: 。代入方程,求得特解系数:
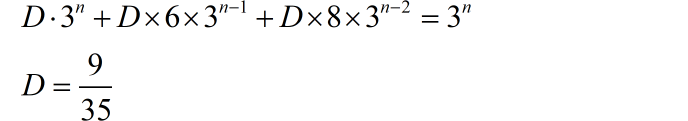
系统的完全解为:
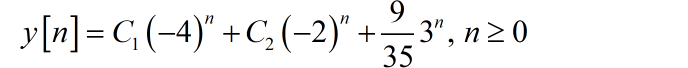
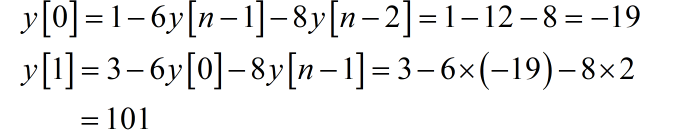
将上述初始条件代入完全解
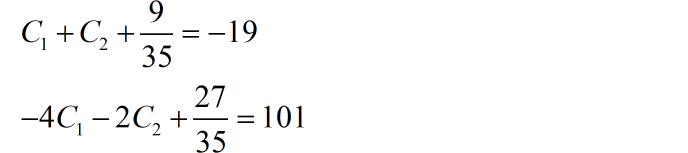
求解方程可得

系统的完全解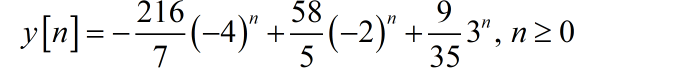
(2)
自由响应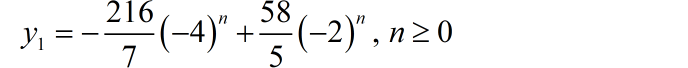
强迫响应
瞬态响应 : 系统中的各个分量都随着n增加而指数增加,所以系统没有瞬态解。
稳态响应 : 系统中各个分量都随着n增加而存在,可以认为都是稳态接。
(3)
可以根据定义分别求出系统的零输入响应,零状态响应。为了为了节省篇幅,这里就直接给出求解结果。
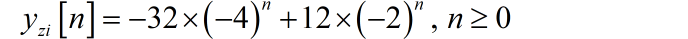
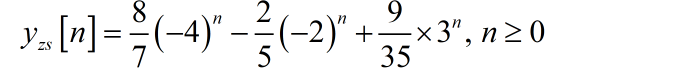

■ 解答:
求齐次解,系统的特征方程为:
对应的特征根为: 。齐次解的一般形式为
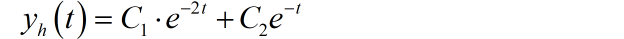
根据输入信号,可以得到对应的特解的一般形式
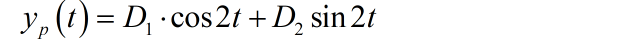
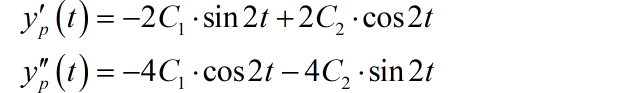
代入方程
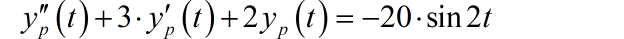
可以得到
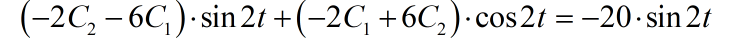
根据方程左右两边不同函数项的稀土相平衡,可以得到
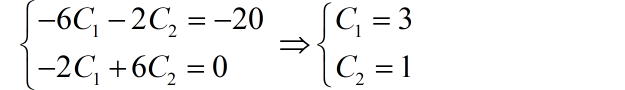
所以特解为
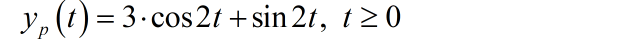
系统的完全解为:
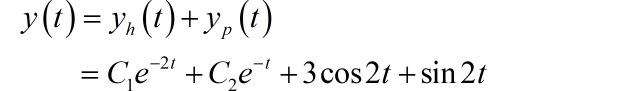
将系统的初始条件 代入完全解,求其中的待定系数,
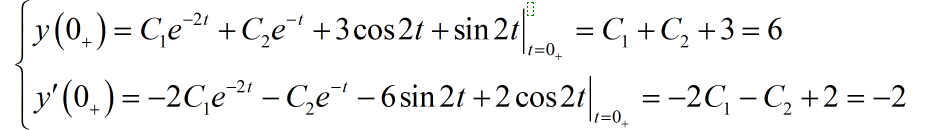
可以求解得到 。所以系统的完全解为:
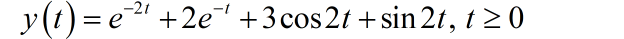

■ 解答:
参见前面第一题中的第3小问。(这个选做题实际上与前面第一小题重复了)

■ 解答:
将 代入微分方程的右边,可以得到
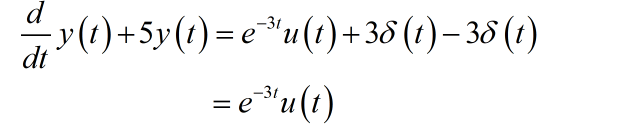
对上述微分方程进行求解。便可以得到系统的单位冲激响应 。中间求解过程省略了,给出最终的答案如下:
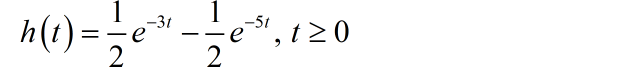
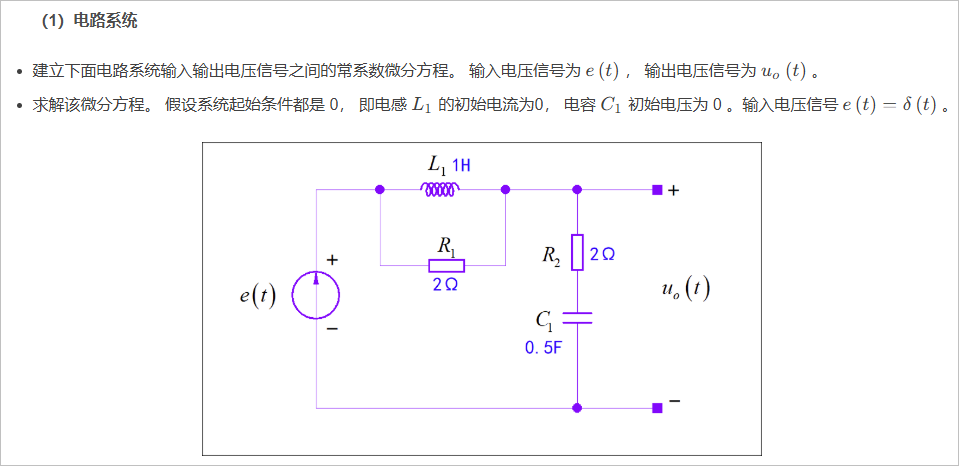
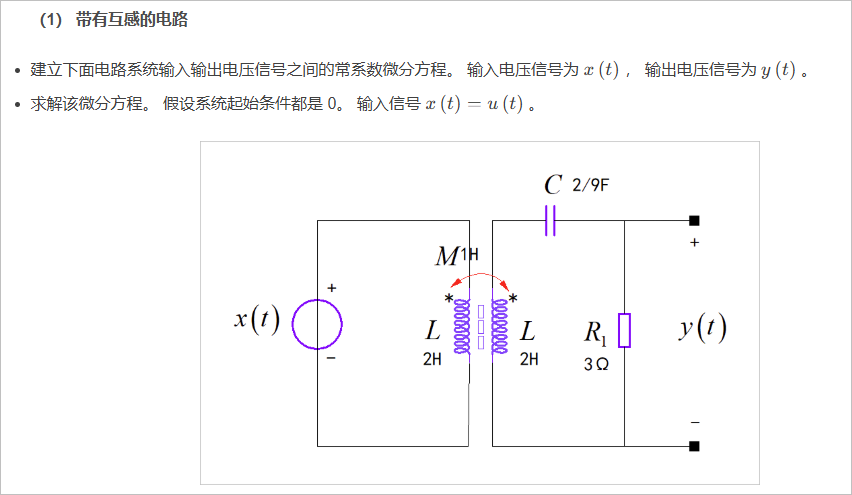
■ 解答:
电路中,R1与L1是并联,它们两端电压相等,所以有:

根据电路中的点数,可以得到
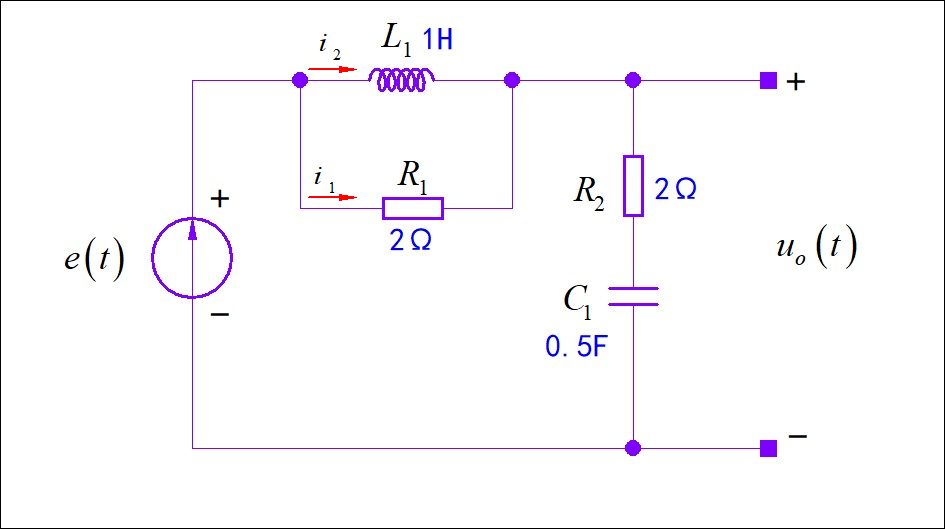
根据电路网络结构,由 KVL,VCR可以得到:
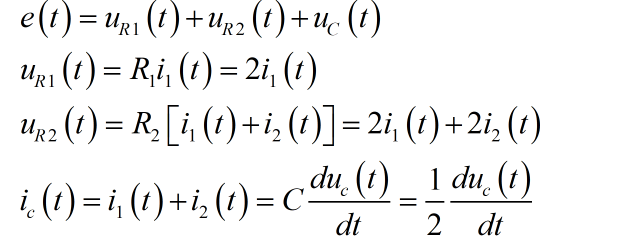
进行化简
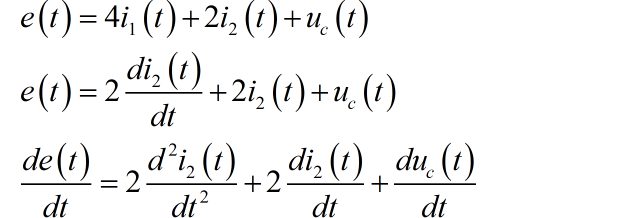
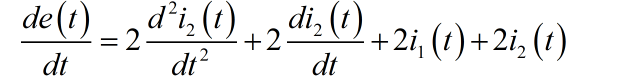
根据前面表达式,先消掉 ,得到 的微分方程
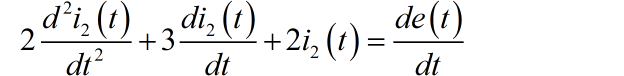
下面,再根据前面的表达式,消去

最终,根据前面的表达式,消去 ,最终整理得到 的微分方程
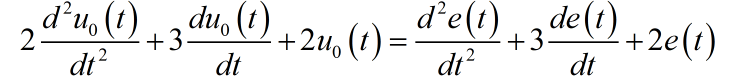
注: 可以采用算子方法或者电路的s域模型来简化微分方程的建立。详细参加一下两个博文:
建立线性动态电路的微分方程[4]
建立电路的微分方程:利用s域模型建立[5]
■ 解答:
本题来自课件 6.1.1.3.2【系统函数应用2】上的例题。
设初级回路电流为 ,次级回路的电流为 。根据 Kirchhoff定理列写回路方程:
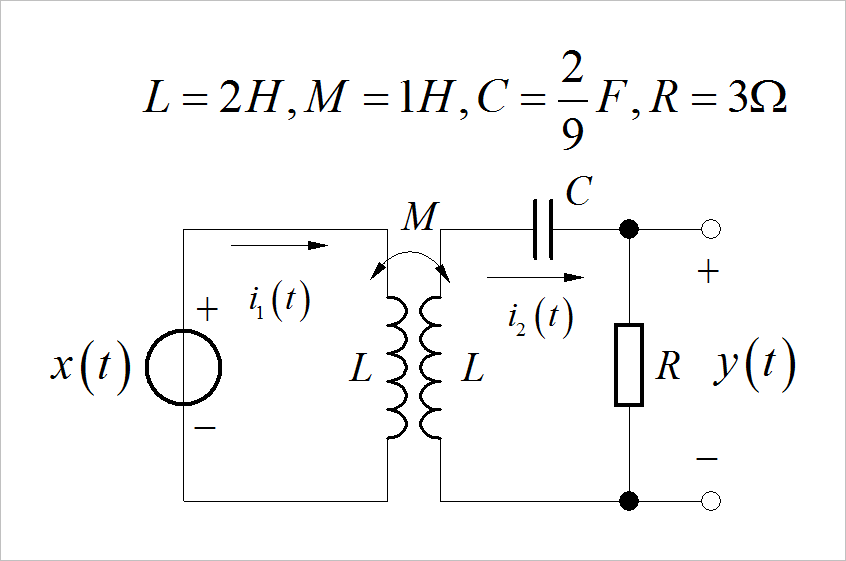
▲ 图1.2.3 设立回路电流之后的电路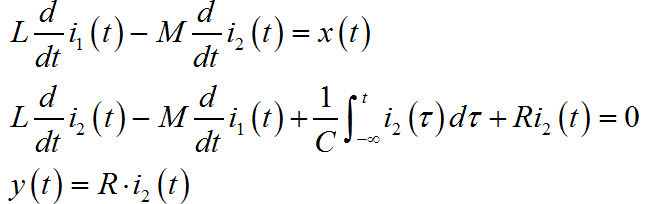
利用算子方法,将上面微分方程修改为算子方程:
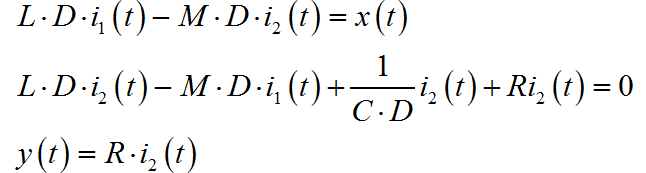
消去其中的 ,可以得到:

对应的微分方程为:
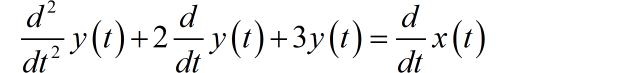
在 的情况下,通过求解微分方程,可以得到 的表达式:
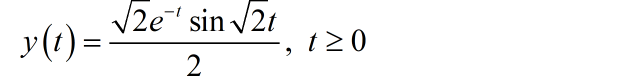
如下是输出信号的波形:
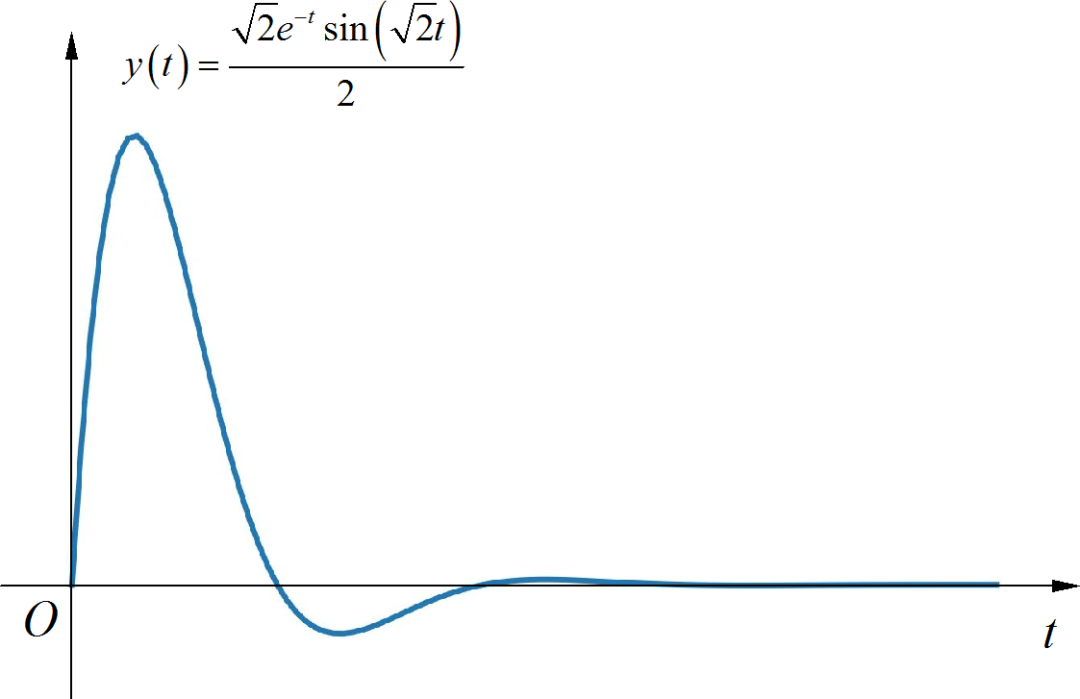
▲ 图1.2.4 输出信号的波形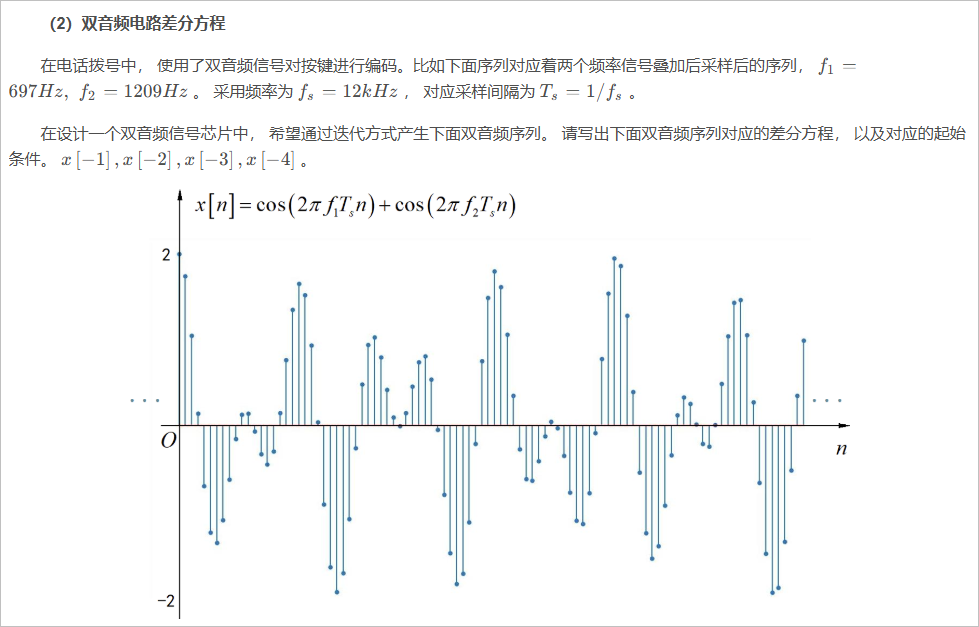
□ 解答:
本题的求解和仿真,可以参见 辅导视频 SS2024-HW3:根据波形建立差分方程[6] 。辅导视频为:
下面给出具体求解结果。序列对应的差分方程为:
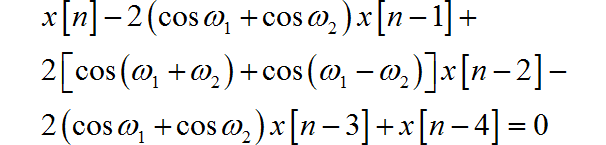
其中 。四个起始条件为:
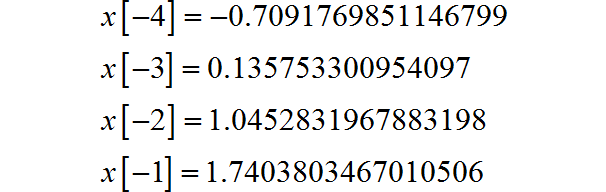
利用上述差分方程和起始条件,便可以产生题目所需要的序列波形。

■ 解答:
(1) 第一小问
根据系统在 u(t) 作用下,系统输出包含有齐次解和特解。根据系统的响应表达式,可以知道,前面两项属于齐次解,后面为特解。由此,可以得到系统差分方程对应的特征方程为:
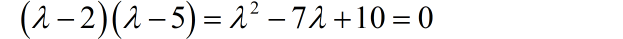
由此,可以确差分方程左边输出信号的表达式。假设差分方程的表达式为
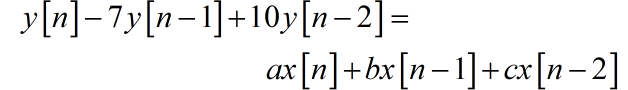
其中 a,b,c 是差分方程 右边输入信号的多项式待定系数。根据已知 ,写出对应的三个方程,可以求解出 a,b,c。
在 n=0 时,根据差分方程以及 的表达式,可以得到
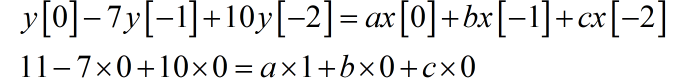
由此,可以得到 。根据同样的道理,分别根据 ,列些出对应的方程,分别求出
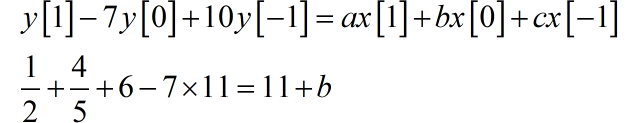
所以 b=-86.7。
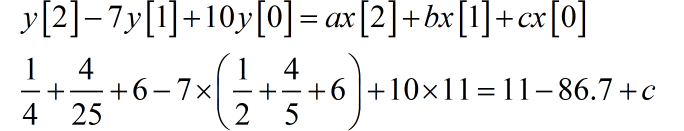
所以 c=141.01。最终可以得到描述系统的二阶差分方程为
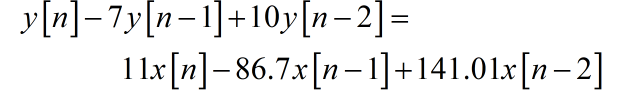
(2) 第二小文
根据系统的 LTI,所以在 作用下所得到的系统输出为
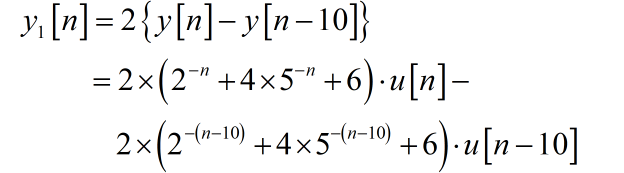

■ 解答:
(1)第一小问
将系统的输出分解成零输入响应和零状态响应。两次结果中的零输入响应是相同的:
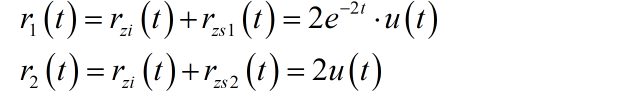
由于系统两次输入信号之间是导数关系,所以两次系统的零状态响应之间也是导数关系

因此,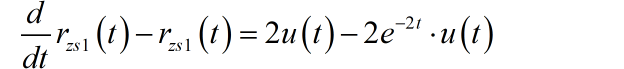
通过求解上述微分方程,可以得到系统的零状态响应
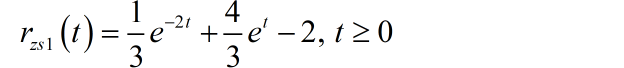
再根据 ,可以得到系统的零输入响应
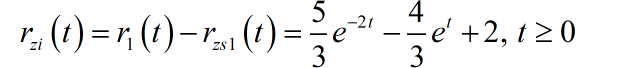
(2)第二小问
由于 ,根据 可以得到系统的单位冲激响应
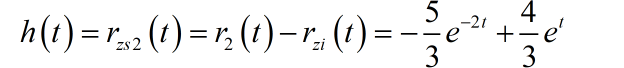
那么,在 作用下,系统的零状态响应为
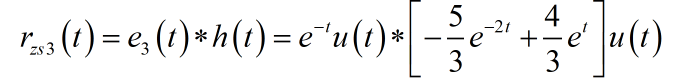
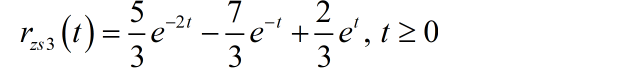
这样,在 作用下,系统的完全响应
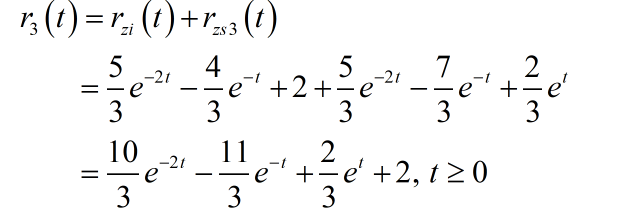

■ 解答:
(1)
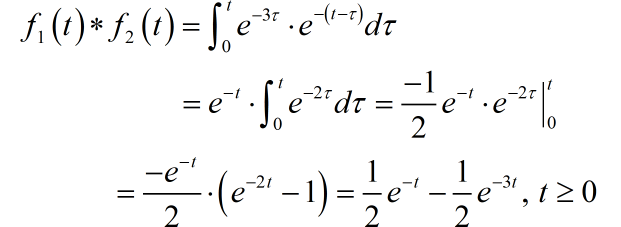
(2)
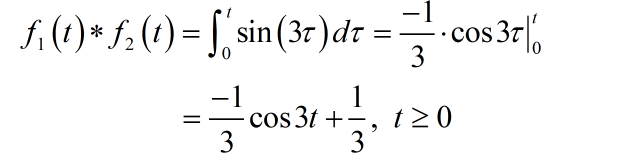
(3)
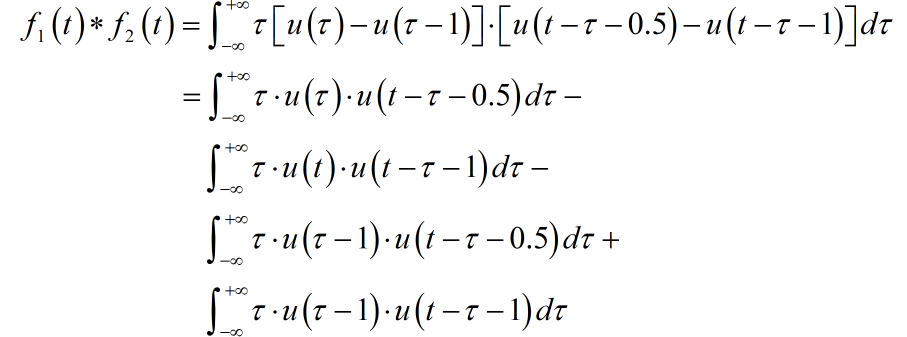
第一部分积分结果:
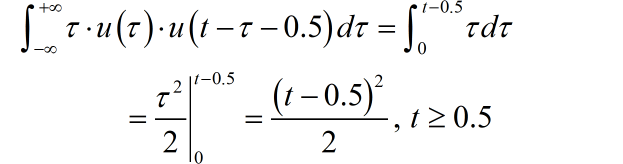
第二部分积分结果:
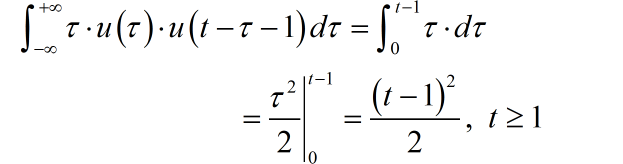
第三部分积分结果: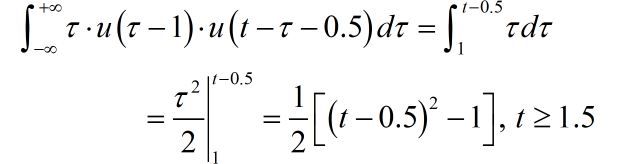
第四部分积分结果:
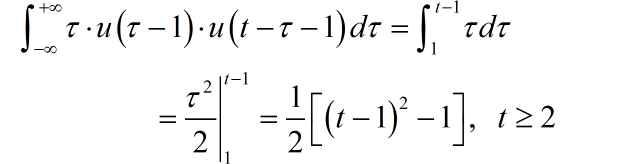
根据不同时间段,合并上面各项多项式,得到卷积结果:
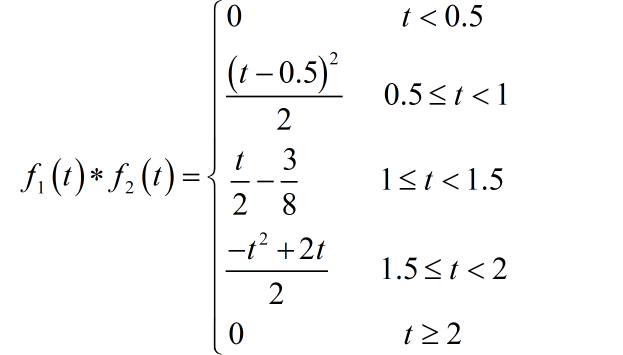
(4)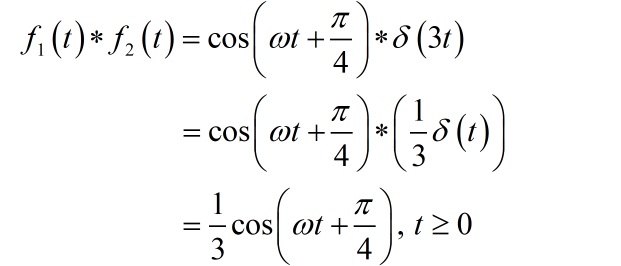
信号与系统2024(春季)作业要求以及参考答案汇总: https://zhuoqing.blog.csdn.net/article/details/136798840
[2]信号与系统2025(春季)作业要求及参考答案汇总: https://zhuoqing.blog.csdn.net/article/details/145879368?spm=1011.2415.3001.5331
[3]信号与系统分析2025(春季)作业要求:第三次作业: https://zhuoqing.blog.csdn.net/article/details/146051212?spm=1011.2415.3001.5331
[4]建立线性动态电路的微分方程: https://zhuoqing.blog.csdn.net/article/details/146140598
[5]建立电路的微分方程:利用s域模型建立: https://zhuoqing.blog.csdn.net/article/details/146138310
[6]辅导视频 SS2024-HW3:根据波形建立差分方程: https://zhuoqing.blog.csdn.net/article/details/136723965