光学史上的那些人儿--- 托马斯·杨
第十八章 托马斯·杨光学
《杨氏光学》
双缝干涉证波澜, 叠加原理破迷团。
测量波长初定量,三色融成七彩梦。
1 杨氏与光的故事
在 18 世纪末的英国米尔维顿小镇,一个名叫托马斯・杨的男孩正用自制的显微镜观察甲虫翅膀。这个自幼展现出惊人天赋的孩子,2 岁识字,4 岁背诵拉丁诗歌,14 岁已掌握十余种语言。谁也不会想到,这个看似文静的少年,日后会成为挑战牛顿权威的科学先驱,甚至被誉为 “最后一个什么都知道的人”。
1773年,伦敦郊外一个寒风刺骨的冬夜,6岁的托马斯·杨蜷缩在父亲的书房里,手指划过古希腊文的羊皮卷。这个已经自学了七国语言的神童,正用一本拉丁文版的《几何原本》打发时间。父亲是位医生兼业余科学家,书房里堆满了解剖标本、棱镜和光学仪器。小杨盯着墙上一束透过棱镜的阳光,突然发现光谱中红、黄、蓝的色带竟与他父亲调配颜料的规律惊人相似——这或许是他与光的第一次“对话”。
16 岁时,他进入大学深造,先后在伦敦、爱丁堡、哥廷根和剑桥等著名学府学习医学。在学医期间,他不仅对医学知识有着深刻的理解,还对解剖学、生理学等领域进行了深入研究,为他后来在科学研究中运用跨学科知识奠定了坚实基础。
青年时期的杨选择追随叔父的脚步学医。在伦敦圣巴塞罗缪医学院,他通过解剖牛眼发现了晶状体调节焦距的秘密 —— 这一发现使他 21 岁便成为皇家学会会员。但他的好奇心并未止步于医学。

1800 年,杨在《声与光的实验和问题》中首次提出 “光可能像声波一样是一种波动”,这一观点如投石入水,激起了科学界的涟漪。
1801 年,杨在皇家学院的演讲中展示了著名的双缝干涉实验。单色光通过两条狭缝后,在屏幕上形成明暗相间的条纹。他向听众解释:“当两束光的波峰相遇时,它们增强;当波峰与波谷相遇时,它们抵消。” 这一现象彻底动摇了牛顿统治百年的 “微粒说”,却也招致激烈反对。《爱丁堡评论》的批评文章称其理论 “充满孩子气的幻想”,但杨并未退缩,他在论文中写下:“我敬仰牛顿,但真理高于权威。”

1803年某个深夜,杨的实验室烛光摇曳。他用硬纸板刺出两道细缝,让烛光穿过后在白墙上投下影子。当预期的两道亮纹间浮现出细密明暗条纹时,他握羽毛笔的手微微颤抖——这幽灵般的干涉条纹,正是光波相消相长的铁证!
这个被后世称为“双缝实验”的装置简陋得令人发笑,却蕴含着颠覆性的力量:若光如牛顿所言是微粒,穿过双缝后应形成两条亮带;而实际出现的干涉条纹,只有波动才能解释。更惊人的是,当杨用不同颜色光源实验时,条纹间距随之改变,他由此推算出红光的波长约为0.0007毫米——人类首次丈量光的波长。

这位倔强的通才开始多线作战:白天行医维持生计,夜晚研究埃及罗塞塔石碑(他后来破译了部分象形文字),抽空还要改进光学实验。1807年,他在《自然哲学讲义》中完善波动理论,首次用“能量”概念解释光强,提出光速在介质中会减速——这些创见直到菲涅尔出现才被重新发现。杨的研究领域远不止光学。并创立了材料力学中的 “杨氏模量”。同时,他对古埃及文明的痴迷促使他破译了罗塞塔石碑上的象形文字,首次揭示了法老名字的拼写规则。
1810年,杨将目光投向更神秘的领域:人类如何感知色彩?当时普遍认为视网膜有无数颜色传感器,他却另辟蹊径:“或许只需三种。”通过让不同年龄患者观察彩色纸片,他发现人眼对红、绿、蓝三色最敏感。这个“三原色理论”不仅解释了色盲成因,更揭示了自然界的精简法则——用三种受体就能构建万千色彩,就像用七个音符谱写所有乐章。
当反对者质问“三种细胞如何证明”,杨微笑回应:“当年伽利略说地球在动时,谁见过地动?”这个超前时代的假说,要等半个世纪后马克斯韦尔用彩色摄影证实,更成为现代显示器RGB技术的源头。
尽管杨的波动理论在生前未获广泛认可,但他的实验为菲涅尔、麦克斯韦等科学家铺路。1829 年,这位 56 岁的学者在伦敦病逝,墓志铭上镌刻着:“他最先破译了数千年来无人能解的古埃及文字。” 1850年傅科测得水中光速变慢,宣告波动说胜利;一个世纪后,爱因斯坦在研究光电效应时,仍引用杨的干涉实验作为波粒二象性的佐证。
今天,当物理教师在黑板上画出那两道决定命运的狭缝,当眼科医生用三原色原理矫正视觉缺陷,当游客在大英博物馆凝视杨破译的罗塞塔石碑副本——不同时空的文明之光,仍在托马斯·杨编织的波动之网中共振。这位终生与权威和成见作战的跨界者,最终用光波在科学史上刻下了永不消逝的干涉条纹。
2 杨氏的光学理论
As this paper contains nothing which deserves the name, either of experiment or discovery, and as it is in fact destitute of every species of merit, we should have allowed it to pass among the multitude of those articles which must always find admittance into the collections of a Society, which is pledged to publish two or three volumes every year. . .
由于这篇论文既没有任何名副其实的实验或发现,事实上也毫无可取之处,我们本应任其混迹于每年必须被收入学会文集的大量文章之中……
19 世纪初英国著名律师、政治家布鲁厄姆(Brougham)在《爱丁堡评论》嘲讽的对象,是托马斯・杨于 1801 年 11 月 12 日和 19 日分两部分向伦敦皇家学会宣读的贝克利安讲座(Bakerian Lecture),该演讲内容后发表于 1802 年的《哲学汇刊》。正是在这场讲座中,杨系统阐述了光的波动理论,提出了广义干涉原理,并以公认的现代形式构建了三色视觉理论。
1802年杨,致安德鲁·达尔泽尔的信中说:
The theory of light and colours, though it did not occupy a large portion of time, I conceive to be of more importance than all that I have ever done, or ever shall do besides.
光与颜色理论,虽说我没在这上面花太多时间,但我觉得它比我以往所做的一切,以及以后要做的其他任何事都更为重要。
2.1光的波动性理论
1800 年 1 月 16 日,托马斯・杨在提交给皇家学会的论文《声与光》中,指出了牛顿体系的缺陷 —— 其中部分问题已被欧拉(1707–1783)等欧洲大陆科学家提及。这些 "细节" 不仅播下怀疑的种子,对杨而言,它们更动摇了整个微粒说的根基。这促使他提出光通过 "以太" 振动传播的波动理论,并将颜色与振动频率关联起来。两年后,他在 1801 年 11 月 12 日发表的《论光与颜色理论》演讲中更加强调这一观点,该演讲逐条对比了他与牛顿在多个概念上的分歧。杨有力地重申了波动理论正确性与自洽性的信念。
Suppose a number of equal waves of water to move upon the surface of a stagnant lake, with a certain constant velocity, and to enter a narrow channel leading out of the lake. Suppose then another similar cause to have excited another equal series of waves, which arrive at the same channel, with the same velocity, and at the same time with the first. Neither series of waves will destroy the other, but their effects will be combined: if they enter the channel in such a manner that the elevations of one series coincide with those of the other, they must together produce a series of greater joint elevations; but if the elevations of one series are so situated as to correspond to the depressions of the other, they must exactly fill up those depressions, and the surface of the water must remain smooth; at least I can discover no alternative, either from theory or from experiment. […] Now I maintain that similar effects take place whenever two portions of light are thus mixed, and this I call the general law of the interference of light.
假设一些相同的水波在静止的湖面上以一定的恒定速度移动,并进入湖的一个狭窄通道。然后假设另一个类似的原因激发了另一组相等的水波,它们以相同的速度和时间到达通道,与第一组水波相遇。一组水波不会毁掉另一组,它们的效果会叠加:如果它们进入通道的方式使得一组波浪的波峰与另一组的波峰重合,它们将共同产生更大的波峰;但如果一组波浪的波峰与另一组的波谷重合,它们会恰好填满波谷,水面将保持平静;至少从理论或实验来看,我没有发现其他可能性。……所以,现在我认为,每当两部分光线以这种方式混合时,会发生类似的效果,这就是我所说的光的干涉定律。
水波的干涉现象很容易演示。杨在 1802 年于皇家研究所的讲座中就用到了水波干涉,他使用了一种自己发明的装置,即现在所说的波纹水槽。这种水槽后来被法拉第使用,并很快成为物理学讲师的标准教具。其基本原理是将水盛在底部为玻璃的水槽中,并从底部照亮水槽,使得水波及其图样在水槽上方的白色屏幕上形成阴影,如图 1 所示。在已发表的讲座中,有一幅著名的图(见图2),展示了两组波纹的干涉。图注这样写道:“从中心 A 和 B 分别向外扩散的两组波浪,以一定方式相互交错,使得在通向 C、D、E 和 F 的直线上,它们相互抵消,水面几乎保持平静”——这就是我们所说的“破坏性干涉”——“而在中间区域则形成波纹”——即“建设性干涉”。如果将两块大小相同的石头同时投入池塘,仔细观察它们扩散开去的波纹,你就能看到这样的干涉图样。
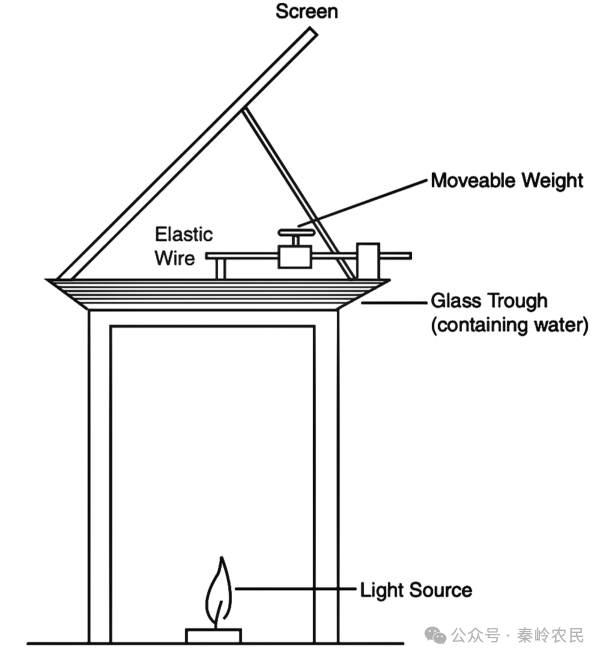
图1涟漪箱用于演示波的干涉
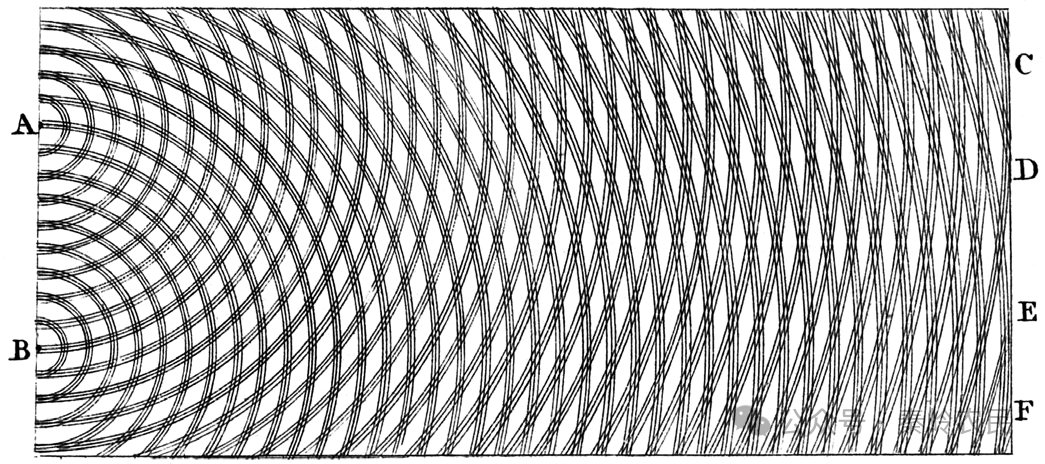
图2 两个水波的干涉,如杨的《自然哲学》所示。
当两列波的波峰相遇时,就会发生波峰干涉。当两列波完全同相位时,或者当它们相差一个、两个或任何整数个波长时,这种情况就会发生。相反,当一列波的波峰与另一列波的波谷相遇时,就会发生波谷干涉。当两列波相差半波长、一个半波长、两个半波长或任何半奇数个波长时,这种情况就会发生。如果改变波长——通过加快或减慢水的波动速度——那么波峰干涉和波谷干涉的位置自然会随之改变。
托马斯·杨意识到,光的波峰和波谷干涉会产生明暗交替的图样,而非水波的波峰波谷干涉产生的光滑与波纹区域。不同颜色的光,其明暗图样的位置会有所不同,因为颜色取决于波长,这是他的假设。实际上,牛顿的理论中并没有红色和蓝色微粒;相反,存在的是波长较长和较短的光波。托马斯·杨认为,这才是对牛顿环颜色现象的正确解释。

图3 牛顿环试验
在牛顿用透镜和玻璃板做的实验中,光线从两个表面反射:一个是空气膜顶部的透镜 - 空气界面,另一个是空气膜底部的空气 - 玻璃板界面(见图3)。托马斯·杨运用光的波动理论和干涉原理,认为牛顿环中的颜色是由于从这两个表面反射的特定颜色光线发生波峰干涉所致。在最内层的红色环中,红色因波峰干涉而增强,其他颜色则因波谷干涉而减弱,因为从空气膜底部反射的光线比从顶部反射的光线多走了整整一个红色波长的距离。第二层红色环中,这束光线比另一束多走了两个波长的距离,以此类推。由于从透镜底部到玻璃板的所有距离都可以根据透镜的曲率精确计算,托马斯·杨找到了测量红光波长的方法。他给出的红光波长是 0.0000256 英寸(650nm),这与现代公认的数值非常接近。牛顿的数据使托马斯·杨能够计算可见光谱中七种主要颜色的波长。这也是首次引入了波长的概念。
干涉效应同样能解释肥皂膜的颜色。光线从薄膜的前表面和后表面反射,当然,由相长干涉产生的色彩鲜艳的颜色取决于薄膜的精确厚度。带有细微刻痕的抛光表面 —— 杨称为 "条纹表面"—— 也会呈现干涉现象:光线从相邻刻痕反射并发生相长干涉,从而产生颜色。我们之前已经提及天然物质的虹彩现象。现代合成材料的一个例子是激光读取的光盘,当人们在日常光照下转动光盘时,其表面会呈现出随角度变化的彩虹色,这取决于光从光盘表面凹槽反射的精确角度。
论点令人惊讶地令人信服。在1802年7月1日的一次演讲中,他进一步完善了这一理论,对一些迄今尚未描述的颜色产生的情况进行了描述,并推导出了一条一般定律:
Wherever two portions of the same light arrive at the eye by different routes, either exactly of very nearly in the same direction, the light becomes most intense when the difference of the routes is any multiple of a certain length, and least intense in the intermediate state of the interfering portions; and this length is different for light of different colours.
当同一束光的两部分通过不同路径(无论完全同向还是几乎同向)抵达人眼时,若路径差为某一特定长度的整数倍,光强将达到最大值;而在干涉部分处于中间状态时,光强最弱。这一特定长度因光的颜色不同而存在差异。
2.2 杨氏双缝试验
杨 1801 年的论文提出了他的波动理论以及光的干涉原理。然而,它并未能提供那种无可辩驳的光的干涉证据,而这类证据对于说服同行科学家是必要的。他尚未拥有类似波纹水槽中交错的水波或音符之间的节拍那样的光学试验证据。他对颜色的解释虽然极为巧妙,但并非唯一的可能解释(尤其是还有牛顿的理论存在)。他需要明确地展示干涉现象;要找到一种实验,这种实验只有一种令人信服的理论解释——即波动解释。
两年后,在完成皇家学院的讲座后,杨终于找到了他一直在寻找的证据。1803 年 11 月,他在《物理光学相关实验与计算》的演讲中公布了这一成果:"在进行伴随阴影的彩色条纹实验时,我发现了一个简洁而有力的证据,能够证明我此前致力于建立的两部分光干涉的普遍规律。因此,我认为有必要向皇家学会简要陈述这些在我看来具有决定性意义的事实。" ,他直接描述了试验:
I made a small hole in a window shutter, and covered it with a piece of thick paper, which I perforated with a fine needle. For greater convenience of observation I placed a small looking-glass without the window shutter, in such a position as to reflect the sun’s light, in a direction nearly horizontal, upon the opposite wall, and to cause the cone of diverging light to pass over a table on which were several little screens of card paper. I brought into the sunbeam a slip of card, about one-thirtieth of an inch in breadth, and observed its shadow, either on the wall or on other cards held at different distances. Beside the fringes of colour on each side of the shadow, the shadow itself was divided by similar parallel fringes, of smaller dimensions, differing in number, according to the distance at which the shadow was observed, but leaving the middle of the shadow always white. Now these fringes were the joint effects of the portions of light passing on each side of the slip of card, and inflected, or rather diffracted, into the shadow. For, a little screen being placed a few inches from the card, so as to receive either edge of the shadow on its margin, all the fringes which had before been observed in the shadow on the wall, immediately disappeared, although the light inflected on the other side was allowed to retain its course, and although this light must have undergone any modification that the proximity of the other edge of the slip of card might have been capable of occasioning. […] Nor was it for want of a sufficient intensity of light that one of the two portions was incapable of producing the fringes alone; for, when they were both uninterrupted, the lines appeared, even if the intensity was reduced to one-tenth or one-twentieth.
我用一枚细针在窗板的小孔上覆盖了一张厚纸,并在其上刺出一个微小的针孔。为了更方便地观察,我在窗板外放置了一面小镜子,将其调整至可将阳光以近乎水平的方向反射到对面墙壁的位置,同时让发散的光锥穿过一张放置在桌面上的卡片屏。我将一片约1/30英寸宽的卡片放入阳光中,观察其在墙壁或不同距离处其他卡片上的阴影。除了阴影两侧的彩色条纹外,阴影本身也被类似但更细小的平行条纹所分割,这些条纹的数量会随观察距离变化,但阴影中央始终呈现白色。这些条纹是卡片两侧透过的光束共同作用的结果——它们被弯曲(或更准确地说,被衍射)进入阴影区域。若在卡片旁放置一个小屏幕,距离卡片几英寸,使其边缘恰好接收阴影的边缘,那么原本在墙壁阴影中观察到的所有条纹会立即消失,尽管另一侧衍射的光线仍可自由传播,且这束光必然经历了卡片另一边缘可能带来的任何干扰。[...] 条纹的消失并非因光线强度不足导致单侧光束无法单独形成条纹;事实上,当两侧光线均未受阻挡时,即使将光线强度减弱至原来的十分之一或二十之一,条纹依然清晰可见。
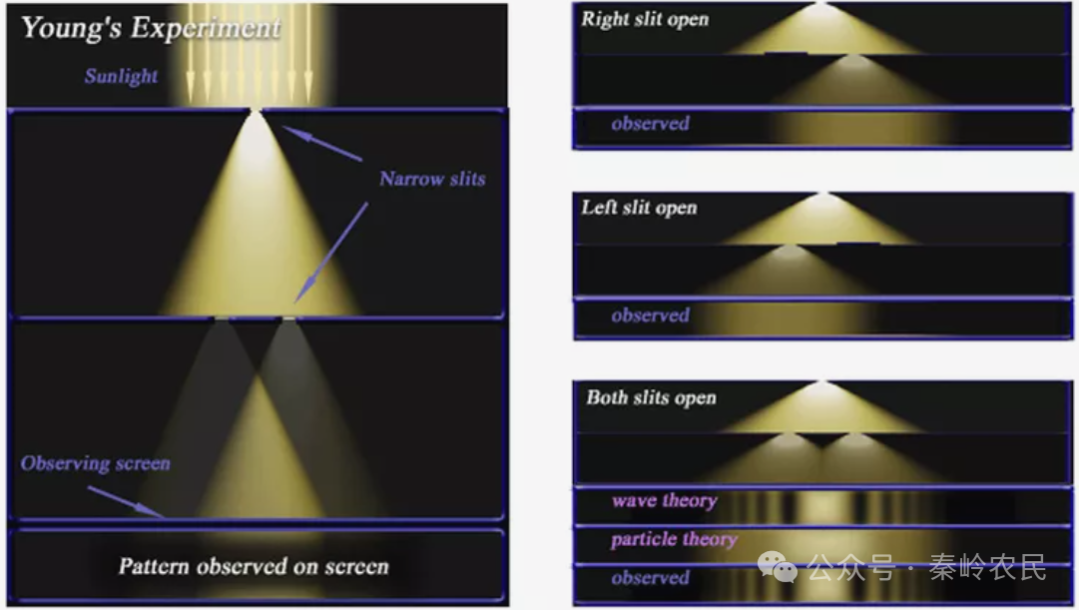
图4 杨氏双缝试验,左边为微粒解释观察屏上的光强为两束光强度之和;右边为波动解释,观察屏上为明暗的条纹。
通过卡片衍射实验,杨计算了不同颜色的光波长,并将其数值与他此前根据牛顿环推算的波长进行对比。他还将其测量的衍射条纹数据与牛顿使用刀口和针尖进行的实验结果进行了比较。实验结果强有力地证明,这些衍射现象和牛顿环的色彩均源于光的干涉,而光的本质确实是一种波。杨的传记作者亚历克斯·伍德在20世纪50年代回顾时写道:“光的波动理论的基础已被牢固奠定。”
2.3眼睛与三原色
1800年11月,杨在英国皇家学会上发表了一篇冗长而详细的论文,题为《关于眼睛的机制》1801年出版的这本书,在一个多世纪后被称为“杰出的专著”,其中包含了“杨对科学最伟大、最具原创性的贡献”。
杨使用自己设计的检测眼镜(optometer)测量了眼睛的折射与调节功能,并发现了自身的散光问题(astigmatism)。他探讨了调节机制的多种可能来源,最终确认调节是由晶状体形状的改变而非角膜形状变化或眼轴长度增加引起的。
My eye, in a state of relaxation, collects to a focus on the retina, those rays which diverge vertically from an object at the distance of ten inches from the cornea, and the rays which diverge horizontally from an object at seven inches distance. For, if I hold the plane of the optometer vertically, the images of the line appear to cross at ten inches; if horizontally, at seven. […] I have never experienced any inconvenience from this imperfection, nor did I ever discover it till I made these experiments; and I believe I can examine minute objects with as much accuracy as most of those whose eyes are differently formed.
我的眼睛在放松状态下,会将来自角膜前方10英寸处垂直发散的光线,以及7英寸处水平发散的光线聚焦于视网膜上。例如,若我将检眼镜(optometer)平面垂直放置,其成像的交叉点会出现在10英寸处;若水平放置,则出现在7英寸处。[...] 我从未因这一缺陷感到不便,也从未意识到它的存在,直到通过这些实验发现。我认为,观察微小物体的精确度,我并不亚于那些眼睛构造不同的人。
杨推断散光是由于散光患者晶状体与垂直轴呈轻微倾斜角度所致,并建议通过倾斜眼镜镜片或望远镜目镜来补偿这一缺陷。尽管这一结论部分正确,但他错误地忽略了角膜在散光中的作用;如今我们已知,角膜缺陷(角膜曲率缺乏对称性,导致不同区域的折射能力略有差异)才是散光的更常见原因,而非晶状体的错位。
杨氏颜色视觉理论,也被称为杨-赫尔姆霍茨三原色理论,是一种开创性的解释,它阐述了人类如何感知颜色。 该理论主要由杨提出,后来由赫尔曼·冯·赫尔姆霍茨完善。该理论认为,眼睛包含三种不同类型的颜色感受器(光感受器),每种感受器对不同范围的光波长最为敏感。 这些感受器大致对应于红光、绿光和蓝光。
Now, as it is almost impossible to conceive each sensitive point of the retina to contain an infinite number of particles, each capable of vibrating in perfect unison with every possible undulation, it becomes necessary to suppose the number limited, for instance, to the three principal colours, red, yellow, and blue, of which the undulations are related in magnitude nearly as the numbers 8, 7, and 6; and that each of the particles is capable of being put in motion less or more forcibly by undulations differing less or more from a perfect unison; for instance, the undulations of green light being nearly in the ratio of 6.5, will affect equally the particles in unison with yellow and blue, and produce the same effect as a light composed of those two species; and each sensitive filament of the nerve may consist of three portions, one for each principal colour.
视网膜的每个敏感点若要容纳无限多的粒子(每个粒子都能与任何可能的波动完全同步振动),这一设想几乎难以成立。因此,必须假设粒子数量有限,例如仅包含三种主要颜色——红、黄、蓝——它们的波动大小比例近似为8:7:6。每个粒子均可被与自身波动频率差异较小或较大的光波以不同强度激发;例如,绿光的波动比例接近6.5,会同样影响与黄、蓝同步的粒子,其效果等同于混合这两种颜色的光。而神经中的每个敏感纤维束可能由三部分组成,分别对应三种主色。
该理论假设人眼有三种不同类型的锥细胞(在明亮光照条件下负责颜色视觉的光感受器)。 每种类型的锥细胞对可见光谱的不同部分最敏感:
·短波锥细胞(S 锥细胞): 对蓝光最敏感。
·中波锥细胞(M 锥细胞): 对绿光最敏感。
·长波锥细胞(L 锥细胞): 对红光最敏感。
任何颜色的感知都取决于这三种锥细胞类型的相对活动水平。 当光线进入眼睛时,它会根据其光谱成分(存在的每种波长的量)以不同的程度刺激三种类型的锥细胞。
大脑通过一个包含各种神经通路的复杂网络来处理这些信号。经过处理后,这些信号会根据它们的强度和组合被解释为特定的颜色:
杨氏理论提供了一个理解不同类型色盲的框架。 当缺少一种或多种锥细胞类型或功能不正常时,就会出现色盲。
杨最初提出了三种感受器类型的想法,但没有具体说明它们对哪些颜色做出反应。赫尔姆霍茨进一步发展了该理论,提供了更详细的解释和实验证据。 他强调了大脑在解释来自三种锥细胞类型的信号中的作用。 这种改进的版本通常被称为杨-赫尔姆霍茨三原色理论。
现代研究在很大程度上证实了杨氏颜色视觉理论的基本原理。 科学家们已经确定了锥细胞中负责其光谱灵敏度的特定蛋白质(视蛋白)。
附18 托马斯·杨简介

托马斯・杨(Thomas Young,1773 年 6 月 13 日-1829 年 5 月 10 日),英国医生、物理学家,光的波动说的奠基人之一,被誉为 “世界上最后一个什么都知道的人”。他在多个领域展现出卓越才华,其成就跨越物理学、医学、语言学、考古学等,甚至涉及艺术与杂技。
1773年出生于英国萨默塞特郡米尔弗顿的一个贵格会家庭。 他从小就展现出非凡的智力天赋,并在很小的时候就开始自学。14岁时已经掌握了拉丁语、希腊语、法语、意大利语、希伯来语、迦勒底语、叙利亚语、撒玛利亚语、埃塞俄比亚语、阿拉伯语和波斯语等多种语言。
1792年,杨开始在伦敦亨特解剖学学校学习医学。
1794年,年搬到爱丁堡,并在同一年写了一篇关于眼睛聚焦方式的论文,年仅21岁的杨成为英国皇家学会会员。
1795年,他在Göttingen学习,在那里他获得了物理学博士学位。
1797年,他进入剑桥大学伊曼纽尔学院,为他进入伦敦内科医学院做准备。同年,他继承了祖父理查德·布罗克莱斯比(Richard Brocklesby)的遗产,这使他在经济上独立了。
1799年,他在伦敦维尔贝克街48号(现用一块蓝色牌匾记录)当上了医生。
1801年,他被任命为伦敦皇家研究所的教授,在那里他发表了一系列关于光学的重要演讲。两年内,他发表了91次演讲。
1803年完成杨氏双缝实验,通过干涉条纹现象证明光的波动性,奠定波动光学基础,并提出三原色理论(红、绿、蓝混合可生成所有色彩)。

1804年6月14日,杨与伊莉莎·麦克斯韦尔结婚,这位聪明的女人一生都理解并支持杨的工作。
1807 年提出 “杨氏模量”(Young's modulus),表征材料弹性性质,成为工程学重要参数。
1811年,杨成为圣乔治医院(St. George’s Hospital)的内科医生。1814年,他被任命为一个委员会的成员,该委员会的任务是考虑将天然气全面引入伦敦所涉及的危险。
尽管取得了成就,杨在生活中还是遇到了一些挫折。他对自己的医生生涯从不满意,总觉得自己达不到行医的要求。由于对他的医疗服务的需求下降,他被迫寻找其他收入来源。
1814年,杨初步破译石碑上的古埃及象形文字,提出其兼具表音与表意功能,并发表相关著作。 杨已经完全翻译了罗塞塔石碑上的“象形文字”(用现代术语来说是通俗的)文本(他有一个86个通俗词的列表),然后研究了象形文字,但没有认识到罗塞塔石碑上的通俗文字和象形文字是希腊文的意译,而不是简单的翻译。1823年,他出版了《象形文字文学和埃及古物的最新发现》。杨的一些结论出现在他为1818年版的《大英百科全书》撰写的著名文章《埃及》中。

在他去世前几年,他对人寿保险产生了兴趣,并于1827年被选为法国科学院的八个外国同事之一。在他的后半生,他把闲暇时间用于破译埃及象形文字的工作,在他去世的时候,他正在编写一本象形文字词典。
1829年5月10日,托马斯·杨在伦敦死于主动脉阻塞。终年56岁,葬于威斯敏斯特教堂。墓碑铭文赞其“几乎在人类所有求知领域都有卓越表现”。