吉布斯现象：你说的，我怎么不相信呢？

一、Gibbs现象

  近期正在给班上的同学讲解傅里叶级数分解的概念，其中包括傅里叶级数分解的收敛性的讨论，吉布斯现象是展示傅里叶级数分解按照误差能量收敛的模式进行收敛，而非一致收敛的典型案例。在第五次作业中，布置了一个实验作业。同学们通过编程，观察矩形脉冲信号傅里叶级数分解的波形收敛的情况，认识到傅里叶级数分解在信号不连续地方，有限项级数合成信号出现的过冲现象，这个现象也被称为吉布斯现象。

二、仿真惹的祸

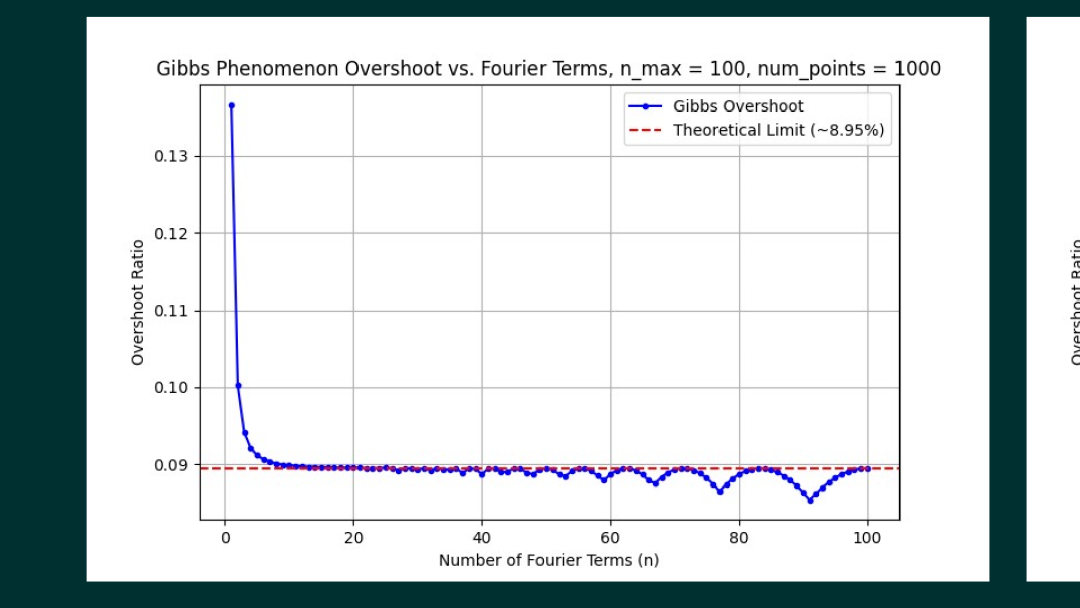
  不出意外，意外出现了。课间，自31班的张章同学给我展示了他在实验中观察的现象。他将傅里叶级数分解合成波形的过冲峰值，按照合成级数项的增加绘制出变化的曲线，可以看到，在合成级数项数从1增加到20 的时候，过冲幅度降低，并且很快达到9%左右，可是随着级数增加，过冲的幅度便出现了波动。可以看到在前100项级数中这个波动已经比较明显。

接下来，他有绘制了 前500项级数过冲峰值的变化情况，这种波动随着级数的增加，变化更加明显，特别是在340级左右，过冲峰值已经降低到3%左右。绘制了前1000项合成波形过冲情况，当级数超过500之后，过冲峰值大小基本上单调下降了。绘制了前5000项的级数波形过冲情况。在超过1000项之后，过冲就没有再超过3%。对此，他怀疑，是否教科书上给出的 Gibbs现象的描述不准确。也就是在信号间断点处，有限项级数波形对应的过冲峰值不是趋于一个常数。

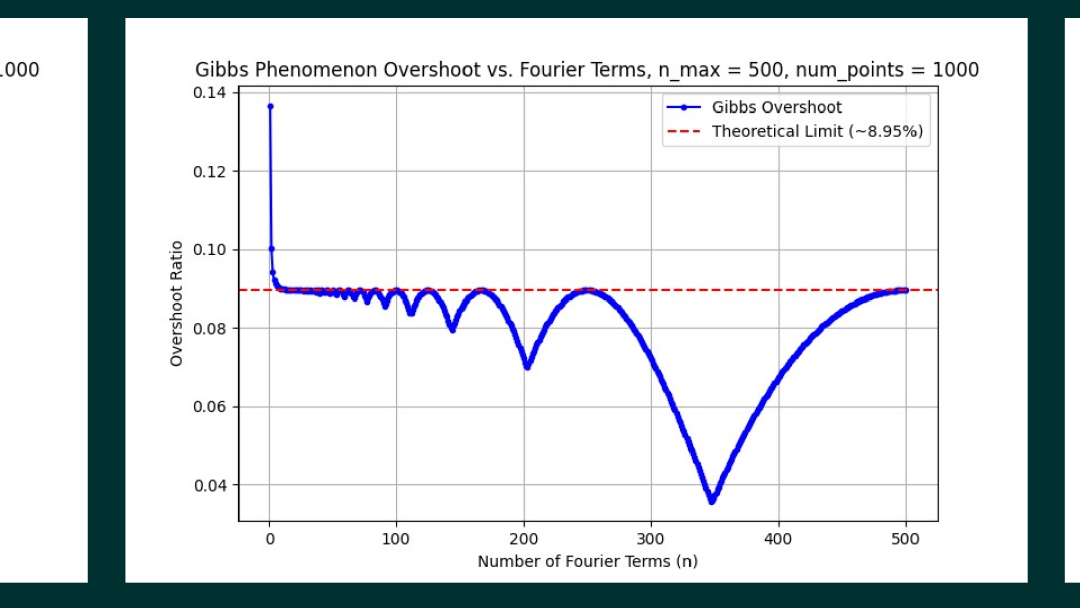
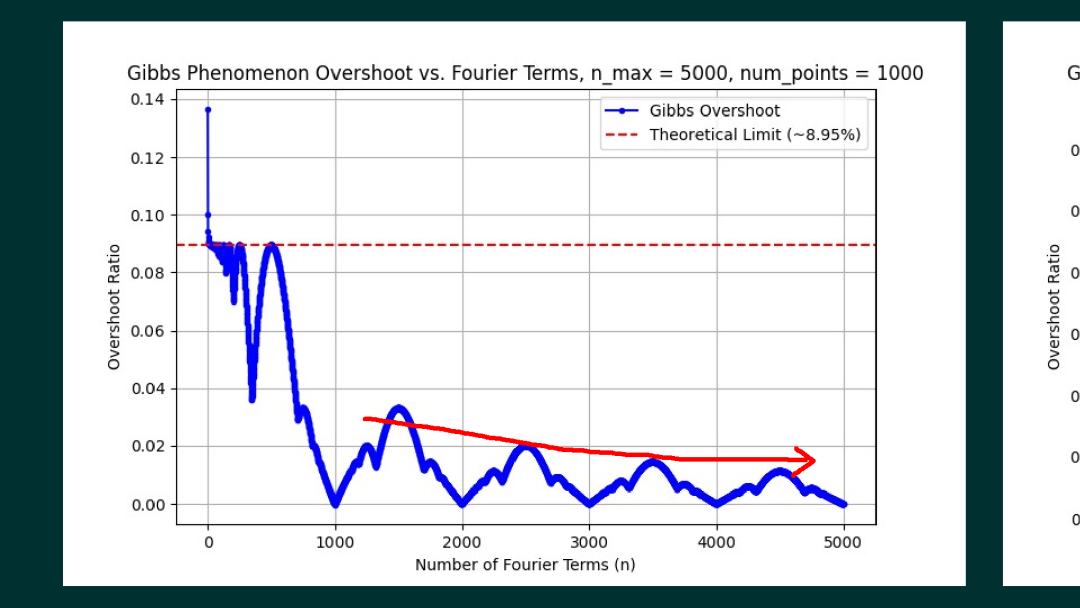
  经过和他的讨论，他理解了数值仿真所得到的信号波形，实际上是对波形的采样。如果采集间隔不足够小，有可能得不到波形的峰值。所以，只要增加波形采样的频率，就可以增加采样到峰值的准确性。现在，他将信号波形的采样，从一个周期中的1000个点，提高到5000个点，同样绘制出前面1000项傅里叶级数波形过冲的幅度，对应的变化就更小了。

不过，后面还是会出现周期性的波动。一不做，二不休，这一次，他将采样数据点数增加到了100k，此时可以看到，在前面1000项傅里叶级数信号过冲基本上都妥妥的等于 9% 。这一下，就彻底放心了。由此可见，仿真只是我们观察和理解客观规律的一个窗口。如果仿真参数设置不当，也会带来一些困惑。

※ 总  结 ※

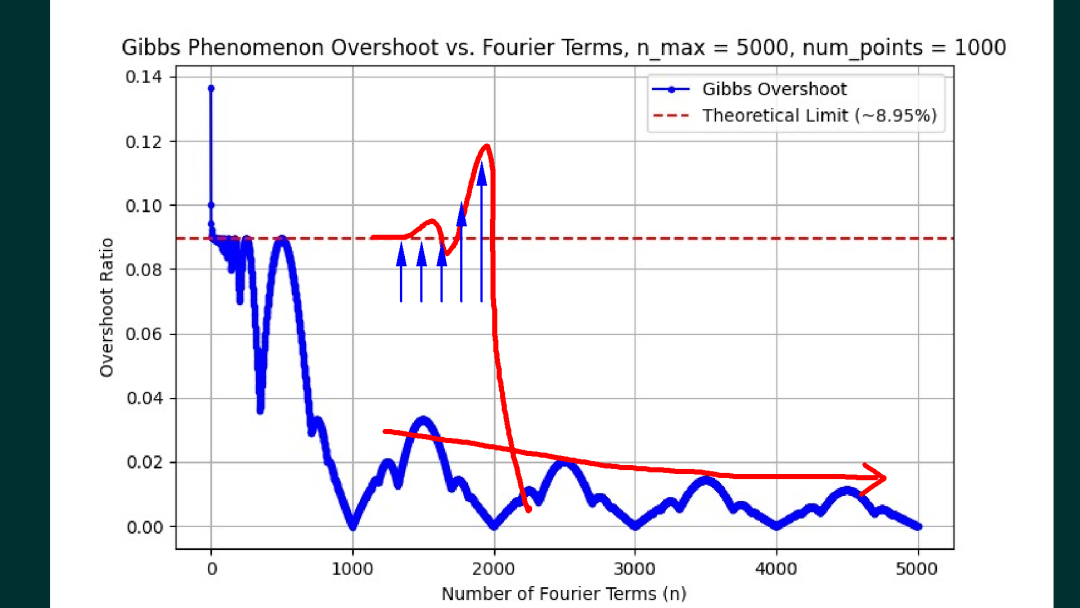
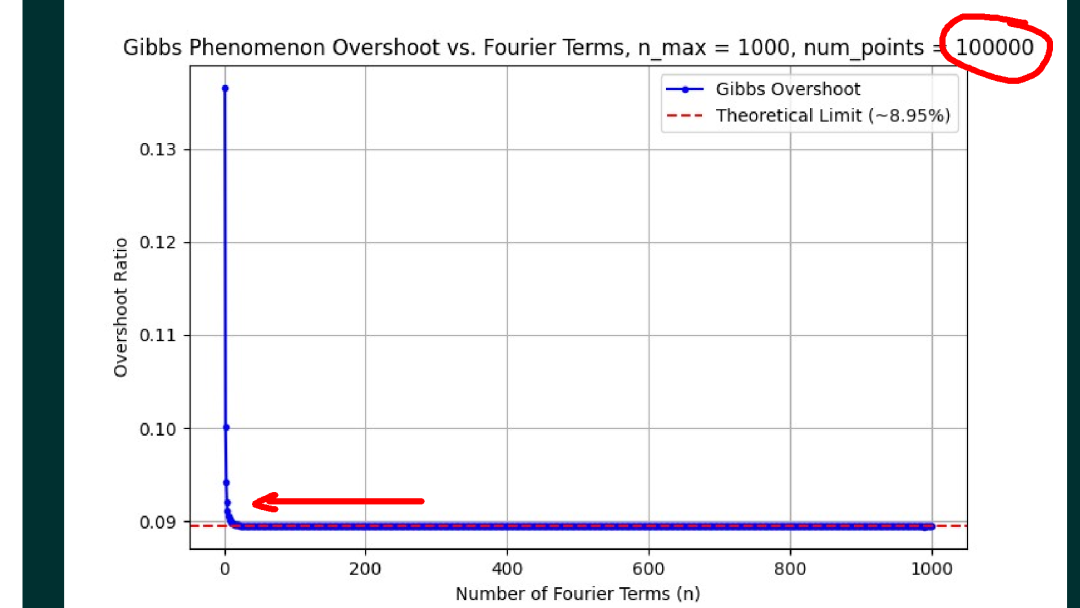
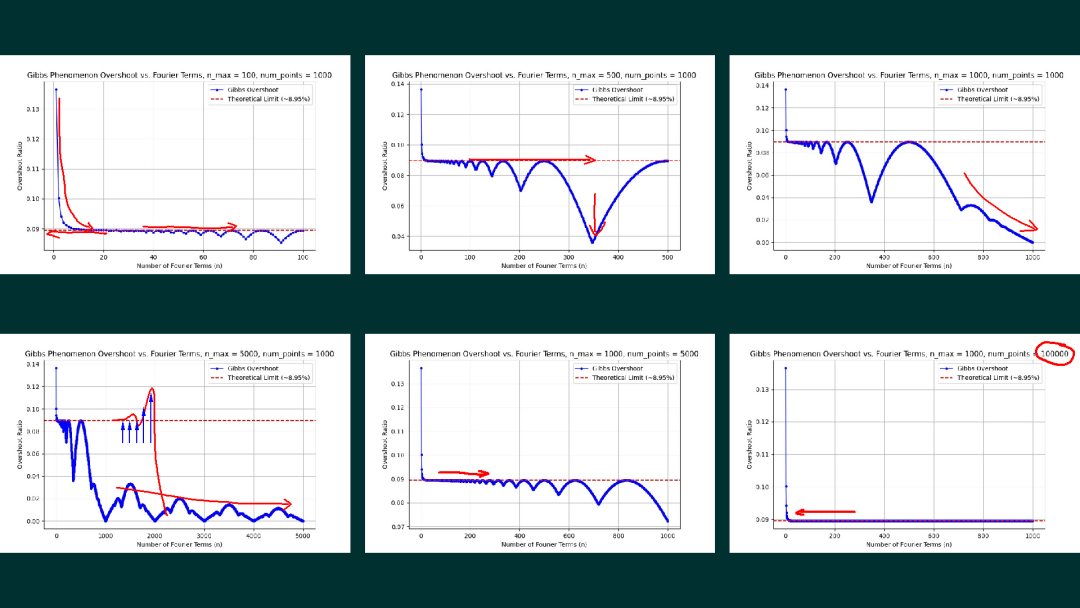
  本文介绍了同学们在Gibbs现象观察实验过程中碰到的现象，讨论了不同的信号采样频率对Gibbs过冲数值的影响。如果将信号的采样频率设置非常高，可以看到，周期信号傅里叶级数有限项合成信号在间断点处的过冲就趋向于 9% 左右。在这里也感谢张章同学对于他的实验结果的分享。