光学史上的那些人儿--- 高斯
第十七章 高斯光学
《高斯光学》
数学探光近轴明,公式推演照乾坤。
透镜排布精微妙,矩阵传输光路明。
1 高斯与光的故事
刺骨的普鲁士寒风呼啸着,年轻的卡尔·弗里德里希·高斯正弓着身子坐在书桌前,烛光在他写满密密麻麻计算的纸页上摇曳。现在是 1801 年,他今晚不是在与小行星或非欧几何作斗争。他正在与一个更加直接,也更加令人沮丧的问题搏斗:透镜。
他心爱的望远镜,是他用自己的双手辛辛苦苦制作出来的,也饱受常见的困扰。图像模糊,色彩失真,他一直在努力将遥远的星星清晰地聚焦。当时,那些以技艺著称的杰出光学师,仍然严重依赖于反复试验。研磨和抛光,凝视和眯眼,希望能偶然发现完美的曲面。这是一个缓慢、昂贵且常常令人失望的过程。
然而,高斯相信一定有更好的方法。他坚信,光线在透镜中的行为可以用数学上的精确性来描述,可以用一套规则来预测和控制它的路径。他对炼金术或猜测不感兴趣;他寻求的是冰冷、坚硬的数字逻辑。
他从最基础的开始:光线在球面上的折射。既定的方程式繁琐而复杂,充满了正弦和正切,即使是简单的计算也成了一场噩梦。他需要一种简化方法,一种能够穿透复杂性并揭示底层结构的方法。
然后,灵感来了。如果他专注于近轴光线呢?那些沿着光轴传播,并且以小角度行进的光线。突然之间,三角函数可以用角度本身来近似表示。一团糟的方程式开始瓦解,揭示了物体距离、图像距离和透镜曲率之间干净而优雅的关系。
他称之为他的“一阶”理论,一种透镜行为的基本蓝图。它并不完美;它没有考虑到困扰现实世界透镜的畸变(像差),但这是一个突破。现在,他可以相对容易地预测透镜的焦距,了解图像是如何放大的,并以几个世纪以来光学师们都无法企及的清晰度来设计简单的系统。
但高斯并不满足于仅仅一个透镜。他设想了复杂的系统,组合在一起的透镜可以相互校正对方的缺陷,从而创造出更清晰、更明亮的图像。挑战在于找到一种分析这些系统的方法,而又不会陷入无休止的计算之中。
他开始尝试一种新的方法,将每个光学元件表示为一个矩阵,这是一个紧凑的数字数组,用来描述它如何改变光线的高度和角度。这是一个抽象的概念,与研磨玻璃的物理现实脱节,但它隐藏着一种强大的力量。通过将这些矩阵相乘,他可以计算出整个透镜系统的总体效果,以惊人的效率追踪光线的路径。
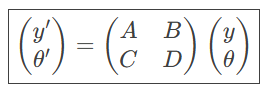
矩阵方法是一个启示。现在,他可以在纸上模拟复杂的望远镜和显微镜,以前所未有的精度预测它们的行为。他可以调整设计,调整透镜之间的间距,并优化系统的性能,而无需触摸一片玻璃。
他用计算填满了笔记本,推导出自由空间、透镜、反射镜,甚至不同材料之间弯曲界面的传递矩阵。他的工作艰苦而细致,但他坚持不懈,因为他深信数学掌握着打开光线秘密的钥匙。
然而,他的发现基本上没有发表。高斯以谨慎著称,他宁愿在与世人分享之前完善他的理论。他使用他的方法来设计和改进他自己的仪器,在他僻静的书房里悄悄地革新着光学领域。
关于高斯非凡能力的消息开始流传开来,由低语的传言和少数有幸瞥见他的仪器的人们传开。他被视为一种科学魔法师,能够以一种令人无法解释的清晰度来变出图像。

直到几十年后,在他去世后,他的完整的光学笔记才最终出版,揭示了他全部的才华。他的高斯光学,凭借其近轴近似和其优雅的矩阵方法,成为了现代透镜设计的基础。光学工程师接受了他的技术,用它们来创造从高功率望远镜到微型相机镜头的一切。
虽然他的理论并没有提供所有的答案——像差问题还需要进一步探索——但它提供了一个框架,一个整个现代光学领域赖以建立的基础。高斯,这位在烛光下工作的安静的数学家,改变了我们看待世界的方式,使星星更加清晰地聚焦,并揭示了微观领域的隐藏之美。他证明了即使是最复杂的物理现象也可以通过数学的力量来理解和控制,从而永远改变了科学和技术的进程。
2 高斯的光学理论
卡尔・弗里德里希・高斯(Carl Friedrich Gauss)在光学领域的研究主要体现在几何光学的数学化和光学仪器设计理论上,其工作深刻影响了光学系统设计的方法论,并为现代光学工程奠定了数学基础。
2.1高斯光学(近轴光学)
高斯提出 "共轴光学系统" 模型:所有折射 / 反射面以光轴为对称轴,光线在近轴区域(与光轴夹角 θ 趋近于零)满足sinθ≈θ、cosθ≈1的线性条件。这一近似将非线性的斯涅耳定律转化为线性方程组,为后续数学建模奠定基础。
高斯光学基于以下四个理论的设想:
1)近轴近似(小角度近似),它假设所有光线都靠近光轴(透镜系统的对称轴)传播,并与之形成小角度。这使我们可以对三角函数进行以下近似:
sin(θ) ≈ θ (其中 θ 以弧度为单位);
tan(θ) ≈ θ;
cos(θ) ≈ 1;
这极大地简化了控制折射和反射的方程式。角度越小,近似越准确。
2)均匀且各向同性的介质,高斯光学假定光线传播的介质(例如空气、玻璃)是均匀的(整个介质都具有统一的特性)并且是各向同性的(特性在所有方向上都相同)。这简化了折射率的计算。
3)清晰的介质界面: 该理论假设不同介质之间的界面是清晰定义的且平滑的。
4)光学器件的尺寸远远大于光的波长,光的衍射效应不起作用。主要考虑光的几何特性。
这种光线从一个空间变换到另一个空间的情况,在数学上可以归结成“共线变换”或“共线成像”的问题,这种共轴理想光学系统理论是由高斯建立起来的,因此人们也把理想光学系统理论称为高斯光学。
高斯证明,就傍轴光线而言,透镜口用基点来代替,光学系统的成像位置和大小可根据这些基点的位置计算出来。具体计算时,使相关角度和光线高度趋近于零,从而将三角公式线性化,推导出一阶公式。因此,高斯光学也被称为“一阶光学”。高斯光学的理论和公式对于光学设计和像差分析具有实用价值。在傍轴区域内,一阶公式是相当精确的。一个经过像差校正的光学系统的性质与一阶公式所描术的性质几乎一致。基于高斯光学理论计算的像可以用来衡量实际光学系统和理想光学系统之间的偏差。
高斯光学(近轴光学)的计算公式是斯涅尔折射定律与几何学的结合,其中近轴近似(小角近似)的关键应用。
根据斯涅尔公式
n₁sin(θ₁) = n₂sin(θ₂) (1)
其中: n₁ 和 n₂ 是两种介质的折射率。 θ₁ 是入射角(入射光线和表面法线之间的角度)。 θ₂ 是折射角(折射光线和表面法线之间的角度)。
近轴近似假设所有角度都很小,因此我们可以近似为 sin(θ) ≈ θ。 将此近似值应用于斯涅尔定律,我们得到
n₁θ₁ ≈ n₂θ₂ (2)
这种线性化的斯涅尔定律更容易处理。
考虑一个由空气(n = 1)包围的、折射率为 ‘n’ 的薄透镜。令 R₁ 和 R₂ 为两个透镜表面的曲率半径。 将斯涅尔定律(以其近轴形式)应用于第一个表面,然后再应用于第二个表面。通过仔细的几何推理,并使用近轴近似,您可以将物距 (s)、像距 (s’)、曲率半径 (R₁ 和 R₂) 和折射率 (n) 联系起来。该过程涉及相当多的代数运算,但最终会得出薄透镜方程:
1/s + 1/s’ = (n - 1) (1/R₁ - 1/R₂) (3)
项 (n - 1) (1/R₁ - 1/R₂) 定义为 1/f,其中 ‘f’ 是透镜的焦距。 因此,薄透镜方程也可以写为:
1/s + 1/s’ = 1/f (4)
透镜制造商公式本质上是薄透镜方程的重新排列形式,用折射率 (n) 和曲率半径 (R₁ 和 R₂) 表示焦距 (f):
1/f = (n - 1) (1/R₁ - 1/R₂) (5)
使用相似三角形和近轴近似,可以将物体高度 (h)、图像高度 (h’)、物距 (s) 和像距 (s’) 联系起来。 这引出了放大率方程:
M = h’/h = -s’/s (6)
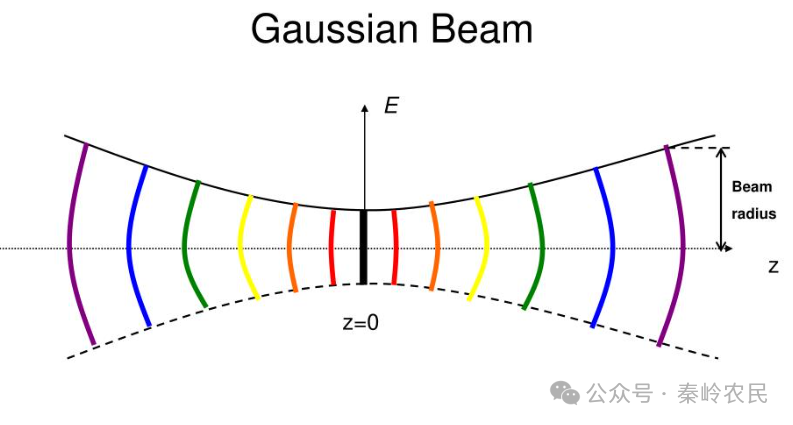
这一理论不仅奠定了几何光学的基础,还为现代激光技术(如高斯光束)、光学工程及计算机图形学提供了理论支撑,展现了高斯将抽象数学应用于现实问题的非凡能力。
2.2高斯矩阵光学
高斯矩阵光学是几何光学中一种基于光线传输矩阵(ABCD矩阵)的分析方法,用于描述光线在光学系统中的传播规律,尤其适用于近轴区(光线与光轴夹角极小)和高斯光束的传输分析。
光线矢量:描述光线在某一截面的状态,定义为列向量:
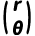
其中:r:光线到光轴的距离(垂轴方向的位置),θ:光线与光轴的夹角(以弧度为单位,近轴近似sinθ≈θ。
ABCD矩阵:描述光线通过光学系统后的状态变化,形式为:
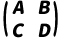
A,B,C,D 为系统参数,取决于光学元件属性的系数。矩阵的行列式AD−BC=1(若系统中所有折射率相同),确保矩阵可逆。
光线经过系统后的新状态为:
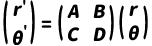
1) 基本光学元件的传输矩阵
自由空间,传播距离为 d,光线变化:
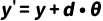
传输矩阵为
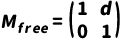
介质为空气,光线角度 𝜃变,位置 𝑟′=𝑟+𝑑𝜃 。
介质为折射率为𝑛透明材料
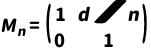
薄透镜(焦距f),光线变化:
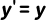
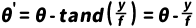
传输矩阵:
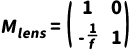
球面反射镜(曲率半径R), 反射后角度变化:𝜃′=𝜃+2𝑟/𝑅。
凹面镜( R > 0)
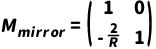
折射界面(两侧折射率分别为 𝑛1,𝑛2 ),角度按斯涅尔定律改变:𝜃′=(𝑛1/𝑛2)𝜃
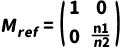
2)复合光学系统的矩阵级联
对于由多个元件组成的系统,总传输矩阵为各元件矩阵的逆序乘积。例如,例如对于一个单透镜系统,光线依次通过自由空间𝑑1、透镜、自由空间 𝑑2的系统矩阵为:
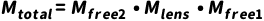
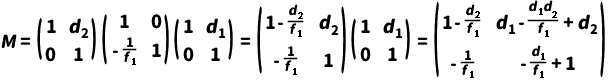
理想光学成像条件(( B = 0)
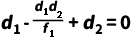
得到
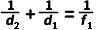
通过高斯矩阵光学,可以方便地计算和分析复杂光学系统的成像特性,如焦距、像差等。这对于望远镜、显微镜等光学仪器的设计和优化具有重要意义。
附17 高斯简介
约翰·卡尔·弗里德里希·高斯(Johann Carl Friedrich Gauss)(1777年4月30日—1855年2月23日)是德国著名的数学家、物理学家、天文学家,被誉为“数学王子”。
他出生于布伦瑞克的一个贫寒家庭,父亲是园丁和工头,母亲是石匠的女儿,未接受过正规教育。高斯自幼展现出非凡的数学天赋,三岁时便能纠正父亲账目中的错误,九岁时便能快速计算1到100的总和,10 岁时已能快速计算等差数列求和。
14岁时,高斯的天赋被不伦瑞克大公卡尔·威廉·费尔南多发现,获得资助进入卡罗琳学院(Carolinum学院,现布伦瑞克工业大学)学习。
1795年进入哥廷根大学。19 岁时成功用尺规作出正十七边形,解决了两千年来的几何难题,轰动学界。
1799年获博士学位。他的博士论文证明了代数学基本定理。
1801年,他计算出了谷神星的轨道,轰动了整个天文学界。
1807 年起担任哥廷根大学教授兼天文台台长,培养了黎曼、戴德金等著名数学家。
1855年2月23日在哥廷根逝世,享年77岁。
高斯在多个领域取得了杰出成就。在数学方面,他提出了二项式定理的一般形式,发展了数学分析理论,并在数论、代数、统计学等领域做出了重要贡献。他的著作《算术研究》奠定了现代数论的基础。高斯提出了正态分布,也称为高斯分布,这是概率论和统计学中最重要的分布之一,广泛应用于自然科学和社会科学中。在物理学领域,他发明了日光反射仪和磁强计,并与韦伯合作绘制了世界第一张地球磁场图。
高斯还致力于天文学研究,担任哥廷根大学教授和天文台台长期间,他在天文学观测和理论方面做出了重要贡献。他的研究成果和科学方法对后世产生了深远影响,成为科学史上的重要人物