光学史上的那些人耳---斯涅耳
第s十一章 斯涅耳光学
《斯涅耳光学》
光行折射费心神, 角度测量细入神。
正弦比例终发现, 定律垂名照后人。
1 斯涅耳与光的故事

刺骨的荷兰风裹挟着大海咸湿的气息,呼啸着掠过沙丘。维勒布罗德·斯涅耳(Willebrord van Royen Snell),裹在厚厚的呢大衣里,全然不顾这寒冷。他的目光紧盯着代耳夫特运河沐浴在阳光下的水面,那是一条闪烁的反射光带。他曾无数次地站在这里,在他父亲房子的边缘,着迷于光与影的嬉戏。
他有一种奇特的痴迷:想弄明白光在穿过不同物质时,究竟如何运动。人人都知道光会弯曲——一个孩子把棍子浸入水中就能看到这一点——但它究竟是如何弯曲的呢?是什么决定了那个角度,入射光线与改变后的路径之间那微妙的舞动?
斯涅耳是受过训练的数学家,他认为答案在于精确的测量。他带着一个黄铜量角器,精心制作的玻璃和水棱镜,以及一种不知疲倦的好奇心,开始了实验。他建造了一个小小的、昏暗的房间,墙壁涂成黑色以吸收杂散的光线。百叶窗上的一个狭窄缝隙让一道阳光刺破了黑暗。

他小心翼翼地将棱镜放置在光束的路径上。入射光线,也就是接触玻璃之前的光线,很容易确定。但折射光线,即通过玻璃后光的改变路径,才是关键。
他花费了几天,甚至几周的时间,一丝不苟地测量这些角度。他会调整棱镜,记录入射角,然后费力地测量相应的折射角。他重复着这个过程,改变着入射光线的角度。他的羽毛笔在羊皮纸上不停地划动,上面密密麻麻地写满了数字,这些数字都经过了他精心的计算和分析。
这些数字起初似乎在跳着一种混乱的吉格舞,没有任何可以辨别的规律。挫败感油然而生。太阳,他在这场舞蹈中的搭档,每天都在降低高度,而荷兰的冬天是无情的。但斯涅耳坚持了下来,他内心确信秩序就隐藏在看似随机的现象之中。
然后在某个阴沉的下午,有了一个突破。他注意到了一些事情,一种微妙但持久的关系。他重新计算了那些数字,那些他早已知道的数字。他拿起他的圆规,在一张新的羊皮纸上,费力地画了一个圆。他画出了入射光线和折射光线,在那里以前只有数字的地方,创造了几何形状。然后他小心地构造了每个角度的正弦。
就在那里。
对于任何给定的两种透明材料——空气和玻璃,空气和水——入射角和折射角的正弦比率保持不变!阳光,曾经是混乱的一团,现在唱出了一首秩序和可预测性的数学歌曲。
他写下了这个优雅的方程:n₁*sin(θ₁) = n₂ * sin(θ₂),一个简单而深刻的真理。他理解到折射率,n,是每种材料的特性,代表着它减慢光速的程度。他知道,这个方程不仅仅是一个数学上的好奇心。它是通往光本质的一扇窗户,是打开隐藏在世界闪烁表面秘密的钥匙。
尽管独自探索,斯涅耳仍然欣喜若狂。他发现了一些基本的东西,一些美丽的东西。他跑出房间,寒冷的空气让他精神焕发。他看向代耳夫特运河,阳光现在似乎以一种新的、有意义的方式跳动着。他看到太阳在水面上的倒影,光的弯曲,不再是随意发生的,而是数学规律优雅的相互作用。
他知道他的工作,即使不被他人看到,总有一天会照亮世界。他的定律,源于耐心和精确,将引导着镜片制造商、天文学家以及任何敢于更仔细地观察光线奥秘的人的手。当他站在那里,风吹过他的头发时,维勒布罗德·斯涅耳明白,即使在浩瀚而有时混乱的宇宙中,只要你知道该往哪里看,秩序和美丽总是会占据上风。
2斯涅耳光学理论
斯涅耳对光学的贡献主要集中在他发现并阐明了折射定律,也就是现在闻名遐迩的斯涅耳定律。他并没有像牛顿或惠更斯那样构建一套全面的“光学理论”,但他的定律是任何光学理论中一个基本要素。因此,理解“斯涅耳光学理论”意味着理解围绕斯涅耳定律的含义和背景。
光的折射定律依然是斯涅耳对科学最重要的贡献,尽管这些定律直到他去世近70年后才发表。托勒密开创了折射的研究,并描述了一条定律来解释折射的程度,但是结果并不总是与他的定律一致。继托勒密之后,阿拉伯科学家阿耳哈曾也研究了折射,但他无法预测光线进入折射率较大的介质时会弯曲多远。
斯涅耳通过观察光在水、玻璃等介质中的偏折现象,结合大量实验数据,发现入射角与折射角的正弦之比为常数。
当一束光线进入玻璃块时会发生弯曲,且弯曲角度取决于光线的入射角。以直线进入玻璃的光不会弯曲,但以一定角度入射时,光线会按与入射角成比例的程度发生弯曲。1621年,斯涅耳发现了入射角与折射角之间存在一个特征比例。斯涅耳定律表明,每种物质都有一个特定的弯曲比例,即“折射率”。折射角越大,物质的折射率就越高。
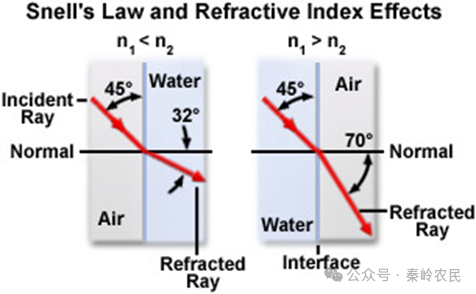
斯涅耳定律可以描述为:
n1 • sin(q1) = n2 • sin(q2)
在该公式中,n 分别代表材料1和材料2的折射率,q 则是光线在这些材料中相对于法线的传播角度。从这个方程可以得出几个重要结论:当n₁大于n₂时,折射角总是小于入射角;反之,当n₂大于n₁时,折射角则总是大于入射角。此外,当两种材料的折射率相等(n₁ = n₂)时,光线将不会发生折射,而是直接穿过材料。
斯涅耳的贡献主要集中在折射这个具体现象上。他没有提供一个更广泛的理论来解释光本身的性质(例如,它是波还是粒子)。 即使它不是一个完整的理论,斯涅耳定律也是光学后续发展的关键基石。它提供了折射的可靠且准确的数学描述,科学家们可以用它来发展更复杂的理论和技术。
“斯涅耳光学理论”并不是一个宏伟的、包罗万象的理论。然而,该定律是现代光学的基石,为理解和操纵光在不同材料中传播提供了必要的数学框架。它的简单性和准确性使其成为几个世纪以来科学家和工程师们持久而宝贵的工具。

附11: 斯涅耳简介
威理博·斯涅耳(Willebrord Snell Van Roijen,1580-1626)是荷兰的数学家和物理学家,曾在莱顿大学担任数学教授。他在光学领域的主要贡献是发现了光的折射定律,即斯涅耳定律。该定律描述了光从一种介质进入另一种介质时,入射角和折射角之间的关系,为几何光学的发展奠定了理论基础。
斯涅耳于1580年6月13日出生于荷兰的莱顿,他的父亲鲁道夫·斯涅耳(Rudolph Snell)是莱顿大学的数学教授。斯涅耳自幼受到良好的教育,主要由他的父亲教授拉丁语、希腊语和哲学。他没有接受过其他正规教育,但在进入大学前已经具备了相当的知识水平。
在1600年,斯涅耳开始在欧洲各地旅行,与多位欧洲数学家和天文学家交流,包括阿德里安·范·鲁门(Adriaan van Roomen)和第谷·布拉赫(Tycho Brahe)。他在布拉格与第谷合作,协助进行天文观测,这段经历对他后来的研究产生了深远影响。
1613年,斯涅耳继承了他父亲在莱顿大学的数学教授职位。他在此期间发表了多部著作,包括《Eratosthenes Batavus》(1617年),其中描述了他测量地球的方法。他还改进了计算π值的古典多边形法,并在光学领域进行了深入研究,发现了光的折射定律。尽管这一发现直到他去世近70年后才由克里斯蒂安·惠更斯(Christiaan Huygens)在1703年发表,但它对现代几何光学的发展产生了重要影响。
1624年,他出版了《提菲斯·巴塔乌斯》(Tiphys Batavus),一部关于航海理论的著作。他在数学方面的工作使他能够提出一种改进的方法,用多边形计算圆周率的近似值。这种方法使用96边多边形,计算出的圆周率值精确到7位,这是对经典方法的显著改进,经典方法只能得到2位。
斯涅耳在1626年10月30日因病去世,享年46岁。他的研究方法和科学态度对后世科学家产生了深远影响,成为科学进步的重要推动力。