什么是双狄拉克模型?
双狄拉克模型是一种快速估算低误码率 TJ(BER) 下的总抖动的工具。抖动信号的确定性和随机子分量在模型范围内分离,以产生两个量,即均方根随机抖动 (RJ) 和峰峰值确定性抖动的模型相关形式 DJ(δδ)。然后根据 RJ 和 DJ(δδ) 估算系统的总抖动。
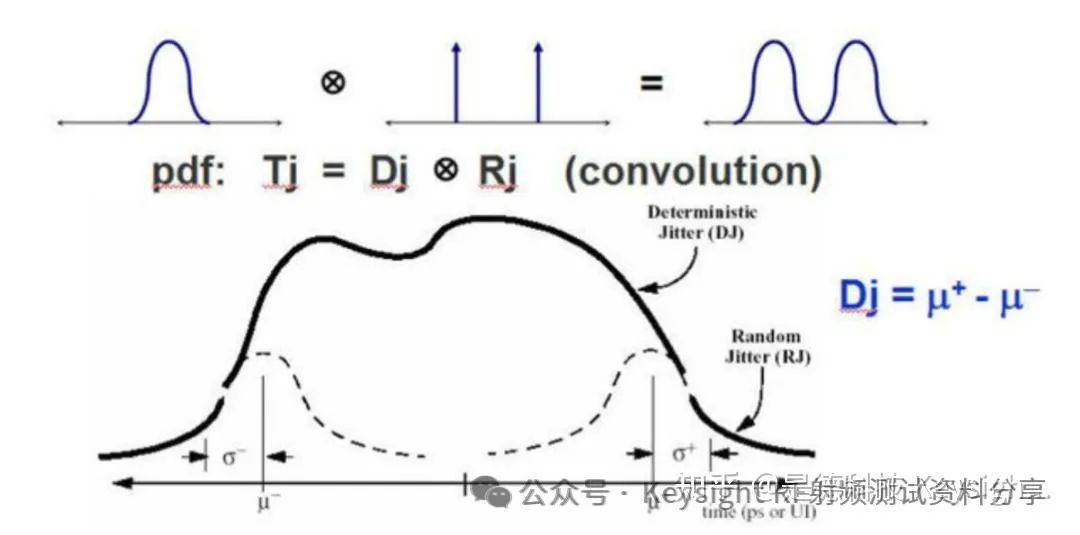
双狄拉克模型因其在快速估计以误码率 TJ(BER) 定义的总抖动方面的实用性以及提供将来自不同网络元素的 TJ(BER) 组合起来的机制而得到普遍接受。它依赖于以下的五个假设。
双狄拉克模型假设
低 BER 下的 TJ(BER) 测量只能在误码率测试仪 (BERT) 上进行,并且需要传输大约 10/BER 位 1 所需的时间(例如,测量 TJ(10–12) 大约需要 70 分钟)。
前两个假设是抖动是由随机和确定性过程的组合引起的,这些过程的分布可以分离,并且 RJ 遵循高斯分布,这是行业范围内的标准假设;它们是双狄拉克模型如何从相对较低的统计数据测量中估计 TJ(BER) 的关键。
抖动的分量通过卷积组合在一起。我们可以认为抖动分布(例如眼图交叉点的直方图)有三个区域:在交叉点处,分布以 DJ 为主;在距离交叉点较远的时间延迟处,分布越来越以 RJ 为主,直到远离交叉点,在渐近极限中,尾部遵循高斯 RJ 分布。分布的渐近尾部通常会导致 BER < 10–8 级别的错误。确定尾部行为(因此,TJ(BER))的理想方法是对 RJ 和 DJ 进行反卷积。但如果事先不知道 DJ 分布,就没有实际的方法来对分布进行反卷积。
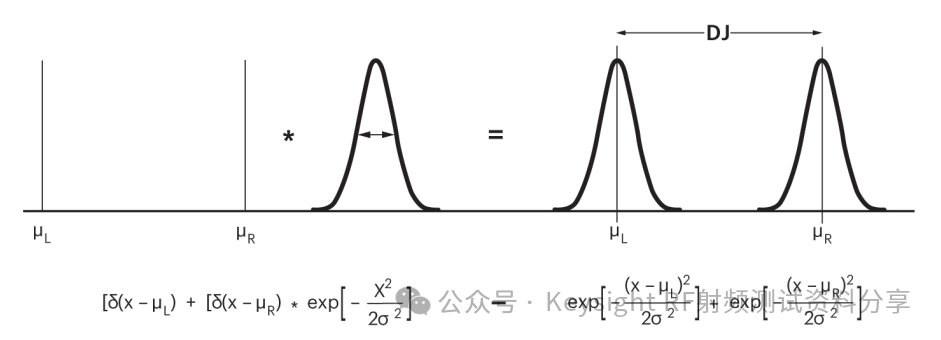
图 2. 两个相隔 DJ 的 delta 函数之和与宽度为 σ 的高斯 RJ 分布的卷积。双狄拉克近似的基本假设是,任何抖动分布都可以通过这种方式建模。
图 2 中的双狄拉克模型提供了最简单的分布:交叉点被分成两个狄拉克-delta函数,分别位于 μL 和 μR,即 DJ 主导区域,然后是人为突然过渡到 RJ 主导尾部。有很多方法可以实现双狄拉克模型,在所有这些方法中,估计 TJ(BER) 都是描述抖动分布尾部的问题,两个宽度为 σ 的高斯尾部相隔一个固定量 DJ(δδ) ≡ |μL – μR|:
双狄拉克模型是对抖动分布外边缘的高斯近似,由 DJ(δδ) 位移。
从概念上讲,认为 DJ 闭合眼图一个固定量 DJ(δδ),而高斯 RJ 尾部闭合眼图的量取决于感兴趣的误码率。一旦测量了 σ 和 DJ(δδ),就可以使用以下公式估计任何 BER 下的眼图闭合情况:
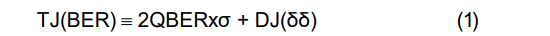
其中 QBER 是根据互补误差函数计算得出的,如表1 所示。由于 σ 乘以 2 QBER,因此 TJ(BER) 的精度首先取决于 RJ 测量的精度 σ,其次取决于 DJ(δδ) 测量的精度。

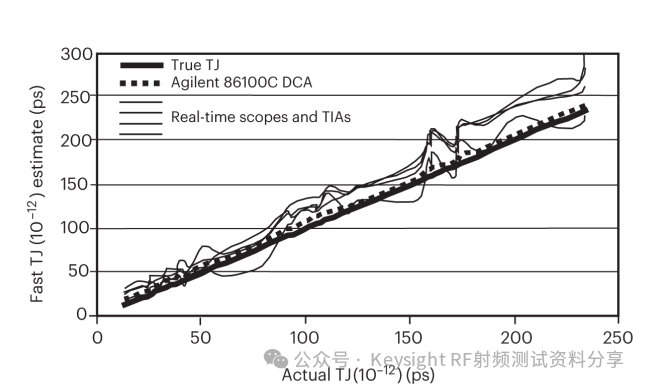
图 3. 不同抖动分析技术在估计各种随机、周期和数据相关抖动组合的 TJ(10–12) 时的比较。粗实线表示实际 TJ(10–12),其他线表示不同测试集的结果。DCA-J(粗虚线)给出最准确的结果。
DJ(δδ) 是一个模型相关量,必须在假设 DJ 遵循由两个狄拉克-delta 函数形成的分布的情况下得出,如图 21 所示。通常,

虽然 DJ(δδ) 总是可以测量的,但 DJ(p-p) 只能在特殊情况下测量。例如,当 DJ 仅由数据相关抖动 (DDJ) 组成时,可以通过比较重复数据模式的平均转换时间来测量。当 DJ(δδ) 被误认为是 DJ(p-p) 的估计值时,不等式 (2) 可能会造成混淆;例如,DJ(δδ) 可能小于 DJ 的一个子分量,但 DJ(p-p) 不能小于它的一个子分量。
不等式 (2) 是双狄拉克模型的结果,但不会降低该模型的实用性。相反,DJ(δδ) 满足标准机构感兴趣的量的两个必要要求:
DJ(δδ) 定义明确且可观测,DJ(δδ) 也可以在各种不同类型的测试设备上测量。另一方面,真正的峰峰值 DJ DJ(p-p) 只能在特殊情况下测量,对估计 TJ(BER) 毫无用处,对诊断问题也没有任何帮助。
当经过深思熟虑的标准提到 DJ 时,它们所指的就是 DJ(δδ),无论是明确还是隐含的。
一旦获得了给定网络元素的 DJ(δδ) 和 σ 值,就可以使用以下规则估计元素组合的值:

简单的规则,即方程 (1) 和 (3),为标准委员会提供了一种在系统组件之间划分 BER 预算的简单方法。请注意,在方程 (3) 中,σTotal 等于平方和,但 DJ(δδ)Total 是 DJ(δδ)i 和的近似值,区别在下面内容中进行了解释。
我们从第 2 节开始,使用一些定义误码率和 TJ(BER) 的背景材料。
第 3 节对双狄拉克模型进行了精确描述,包括 Q 尺度表示,以及该模型如何提供一种简单的技术来组合不同网络元素的 TJ(BER) 来估计系统的 TJ(BER),即方程 (3)。
在第 4 节中,我们讨论了该模型的不同实现,找出了常见的缺陷,并展示了特定系统中 DJ(δδ) 和 DJ(p-p) 之间的关系,以及在简单的双狄拉克实现中 σ 和 TJ(BER) 的估计准确度。在第 5 节中,我们最后讨论了行业标准假设的准确性,并进行了简要总结。
根据比特误码率BER定义的总抖动
不相关的抖动分布通过卷积组合。业界普遍认为,随机抖动 (RJ) 遵循高斯分布,与所有 DJ源无关。概率密度函数或抖动分布可以通过制作眼图交叉点的直方图(图 4a)来测量。抖动分布 J(x)(图 4b)可以描述为 RJ(x)_DJ(x),其中 DJ(x) 的函数形式通常不为人所知,甚至无法观察到,但 RJ(x) 由高斯分布给出,其宽度为 σ,x 是时间延迟或眼图的水平轴。
如果我们将抖动分布写为
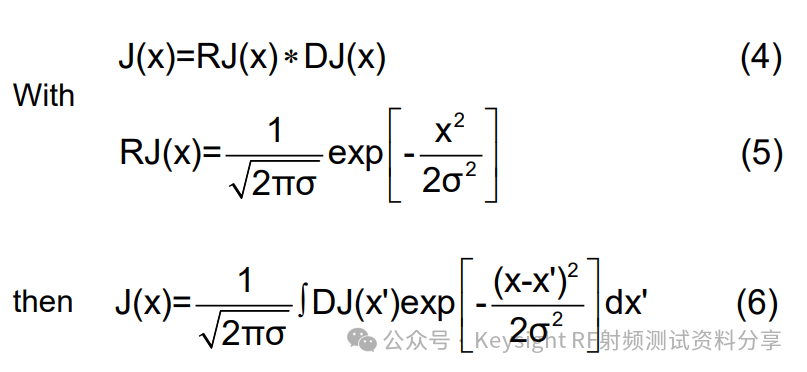
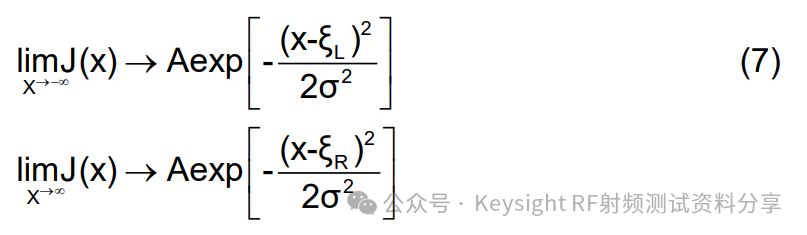
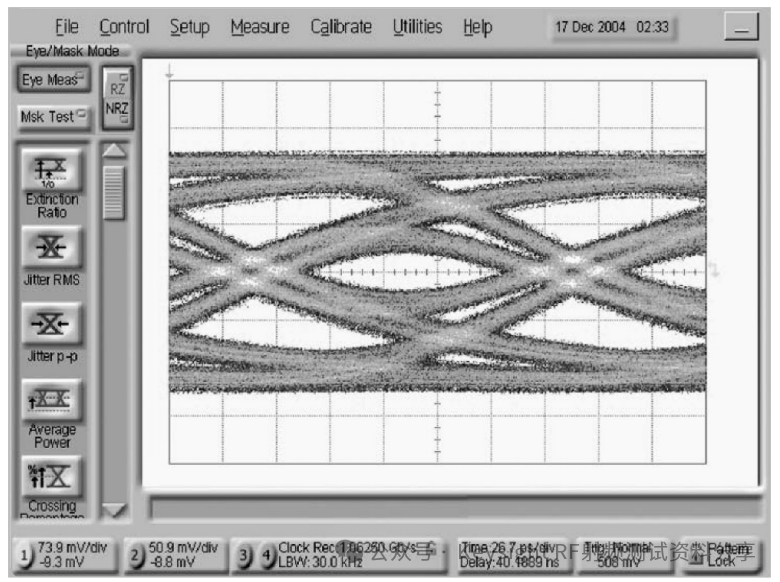
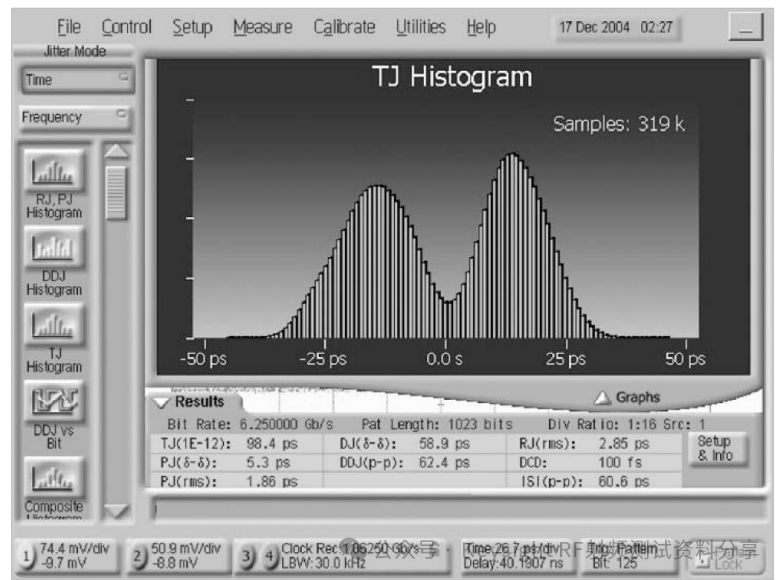
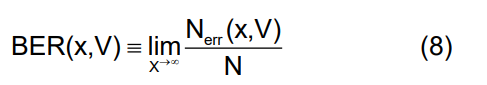
其中 (x, V) 是采样点的位置,而 Nerr(x, V) 是从总共 N 个传输位中检测到的错误数。例如,如果在采样时间延迟 x 时观察到的电位(或者,对于差分信号,差分线路上两个电位的差)大于 V,则在逻辑“0”位上检测到错误。在本文档中,我们假设所有错误都由时间误差(即抖动)单独导致,这意味着我们可以测量 BER 对时间延迟 x 的依赖性,而不必担心幅度噪声。
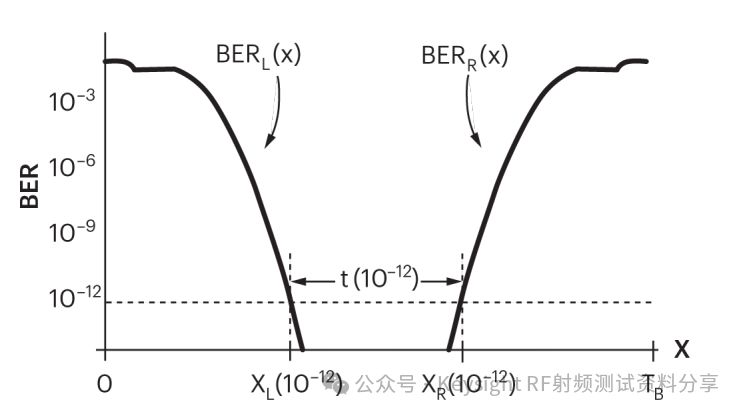
图 5. 浴盆图或 BERTscan;误码率作为采样点延迟 x 的函数。
BER 对 x 的依赖性是 TJ(BER) 定义的核心。通过扫描眼图上采样点的时间延迟位置,可以在误码率测试仪上测量浴缸图 BER(x),如图 5 所示。BER(x) 也可以从抖动分布 J(x) 中得出。由于 BER(x) 由跨采样点时间位置 x 波动的逻辑转换概率给出,如果我们考虑图 4a 的左边缘,则跨点 x 波动的转换概率由下式给出
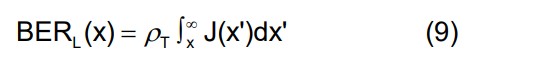
其中 ρr 是逻辑转换数与总位数的比率,即转换密度。
同样,在眼图右侧,靠近 x = TB,
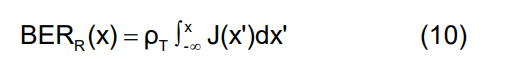
以便

给定 BER 下的眼图张开度 t(BER) 由给定 BER 下的左 BER 曲线和右 BER 曲线的分离给出。例如,在图 4 中,BER = 10–12 下的眼图张开度由 xL 和 xR 之差给出 - 即 BER = 10–12 的点。正式地,如果我们反转 BER(x) 以得到 x(BER),那么
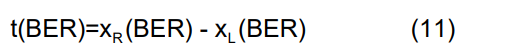
TJ(BER) 定义为在给定 BER 下由于抖动而导致的眼图闭合量;也就是说,TJ(BER) 是比特周期与眼图张开之间的差值:
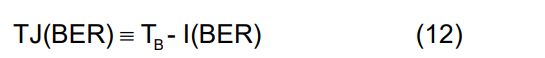
双狄拉克模型的实际应用
双狄拉克近似背后的基本假设是,任何确定性抖动分布都可以通过两个相隔 DJ 的 delta 函数来近似。在这种特殊情况下,DJ(δδ) = DJ(p-p)。紧随双狄拉克的抖动分布可能是纯占空比失真 (DCD) 或方波相位调制的结果,但在实际应用中,它要复杂得多。
单独的抖动分量通过卷积组合在一起——将一个分布折叠到另一个分布上的数学过程,等式 (6)——了解卷积过程非常重要。为了说明 RJ 和 DJ 如何卷积,可以将平滑的高斯 RJ 视为施加在有界 DJ 分布上的涂抹函数。
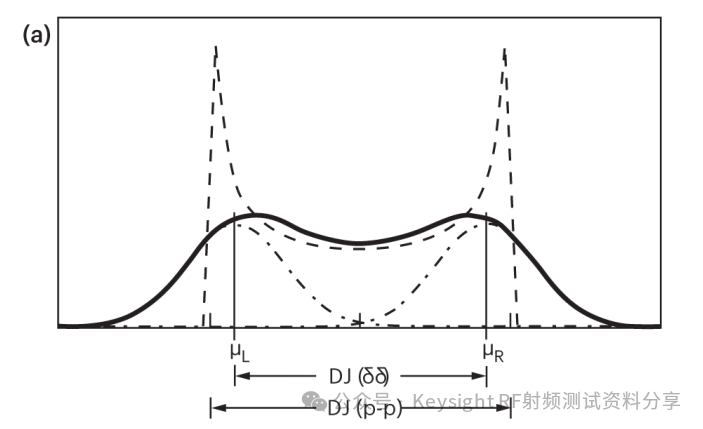
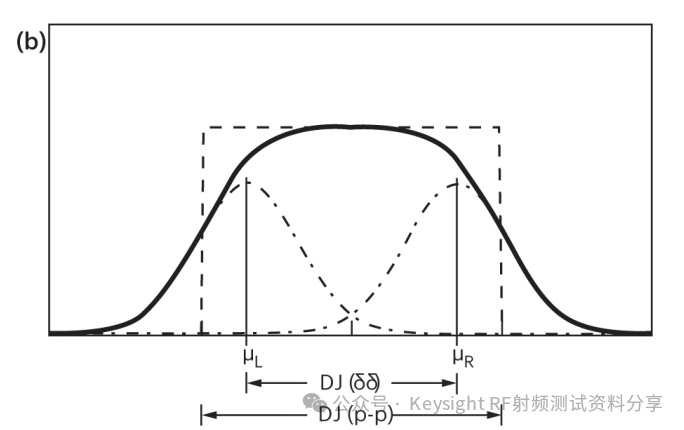
图 6. 双狄拉克模型在两种理想情况下的应用。在 (a) 中,虚线 DJ 分布由单一频率的正弦抖动引起,在 (b) 中,虚线有界、恒定(方波)DJ 分布可能由三角波相位调制引起。在这些示例中,σ = 0.15xDJ(p-p),实线是卷积抖动分布,虚线点线是双狄拉克近似。垂直线表示双狄拉克模型设置高斯均值 μR 和 μL 的位置
在图 6a 中,虚线 DJ 分布由单个频率的正弦抖动给出,在图 6b 中,由平坦的有界 DJ 分布给出。DJ 分布与高斯卷积产生平滑的实线。卷积的效果是平滑 DJ 分布的尖锐边缘,并且 J(x) 获得其高斯尾部。请注意卷积的平滑效果如何将尖锐的 DJ 边缘向内带走。
图 6 中的垂直线设置在 μR 和 μL 处,表明不等式 DJ(δδ) = |μR – μL | < DJ(p-p)。两个高斯曲线(点划线)给出了实线的双狄拉克近似。双狄拉克分布的中心部分与实际分布不匹配并不重要;重要的特征是高斯尾部与真实抖动分布的尾部匹配,如公式 (7) 所示,因此可以使用公式 (9) 至 (12) 估算 TJ(BER)。
需要更多信息,您可點擊:抖动分析:双狄拉克模型

本文提供了双狄拉克模型的完整描述、它在技术标准中的使用方式以及它在不同类型的测试设备上的应用方式的摘要。详细描述了 Q 尺度公式,用于提供模型特征的简单视觉描述,并展示模型的不同实现如何导致不同的结果。有关抖动分析的介绍,请参阅参考资料。
双狄拉克模型是一种快速估算低误码率 TJ(BER) 下的总抖动的工具。
抖动信号的确定性和随机子分量在模型范围内分离,以产生两个量,即均方根随机抖动 (RJ) 和峰间确定性抖动 DJ(δδ) 的模型相关形式。然后根据 RJ 和 DJ(δδ) 估算系统的总抖动。
本文提供了双狄拉克模型的完整描述、它在技术标准中的使用方式以及它在不同类型的测试设备上的应用摘要。详细描述了 Q 尺度公式,用于提供模型特征的简单视觉描述,并展示模型的不同实现如何导致不同的结果。
双狄拉克模型:
• 提供一种快速估算低 BER 下的 TJ(BER) 的有效方法。
• 建立在 RJ 遵循高斯分布的假设之上,该分布可以用单个参数 σ 来描述
• 定义可观测的 DJ(δδ),该 DJ(δδ) 可以通过多种不同的方式测量,但不应与真正的峰峰值 DJ DJ(p-p) 混淆。通常,DJ(δδ) < DJ(p-p)。
• 提供一种透明的方法来结合不同网络元素的 σ 和 DJ(δδ) 来估算系统的 TJ(BER)。
• 提供可观测的、定义明确的量以用于技术标准。
• 可以以不同的方式应用,这些方式具有不同的系统不确定性,可能导致不同的错误,从而使结果的比较变得困难。
• 最准确地实现方法是通过 Keysight 86100C DCA-J 中引入的技术,该技术结合了与测试模式相关的抖动硬件分离和与定时噪声 σ 的直接测量不相关的抖动。