【光电智造】一文读懂显微镜的分辨率与衍射极限

之前我在文章中谈论过图片以及显示器的分辨率，这种分辨率往往与像素有关，为：横向像素数量*纵向像素数量。

然而，对于显微镜，‘分辨率’是指另一个概念：

视野中两个能被区分的实体点之间的最小距离。

小白可能会问，既然是两个分开的小点，只要放大倍数足够大不就可以区分吗？

实际上，对于光学显微镜，成像分辨率往往卡在200nm左右，这也是光学显微镜研究者常说的衍射极限。

为什么会有这个衍射极限？接下来我将一步步说明。我尽力通俗易懂，让小白也能很快明白。

1. 圆孔夫琅禾费衍射图样与艾里斑

我们不用管夫琅禾费是谁，只需要知道，我们高中就学过光具有波粒二象性。既然光具有波的性质，那就会有衍射。从圆孔出来的光不是平行光，而是像水波一样会有干涉和衍射。

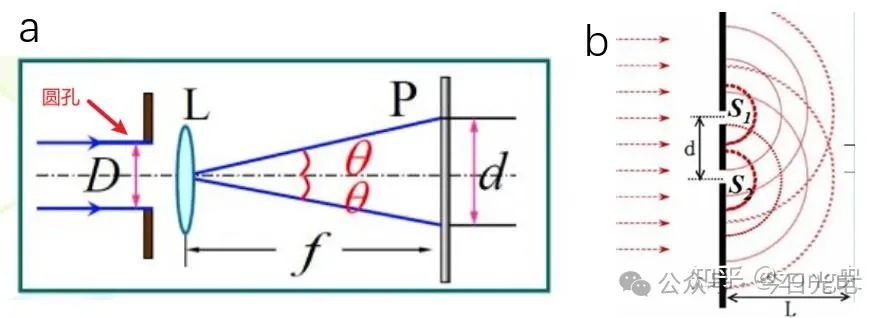
因而，对于点光源，经过圆孔和透镜聚焦成像之后会是这个样子：

显然，从结果上看，并不是一个无限小的点，而是由中心斑点和一个个圆环组成。

什么是艾里斑？

艾里斑：点光源通过理想透镜成像时，由于夫琅禾费圆孔衍射而在焦点处形成的光斑。中央是明亮的圆斑，周围有一组较弱的明暗相间的同心环状条纹，把其中以第一暗环为界限的中央亮斑称作艾里斑。

2. 艾里斑如何影响分辨率？---瑞利判据

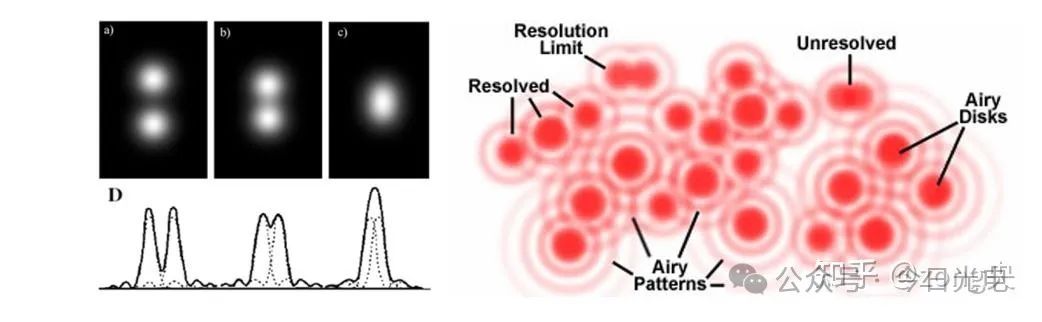
观察上述图像，显然，当两个艾里斑离得过近时，我们很难分清是一个、两个、还是多个斑点在一起。

什么情况下可以区分？

瑞利判据：当一个圆斑像的中心刚好落在另一圆斑像的边缘（即艾里斑边缘）上时，被认为刚刚能被分辨。

所以，能区分开的两个艾里斑，中心点距离会大于艾里斑的半径。

艾里斑的半径怎么计算？

下面我给出了公式。具体的数学推导省略。（虽然我也想装逼，但是这里真不会）

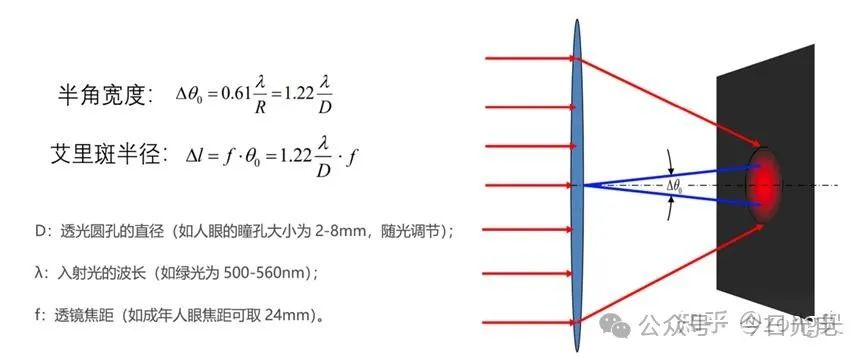
到此，我们知道了在艾里斑的基础上，相距多远时才能够区分。与圆孔直径、入射光波长、透镜焦距有关。

3. 光学显微镜的分辨率极限

还记得上面显微镜分辨率的定义吗？ 结合瑞利判据，对于显微镜而言，分辨率极限就是艾里斑的半径。

显微镜的分辨率公式，可由艾里斑半径公式推导而来（推导过程省略），如下：

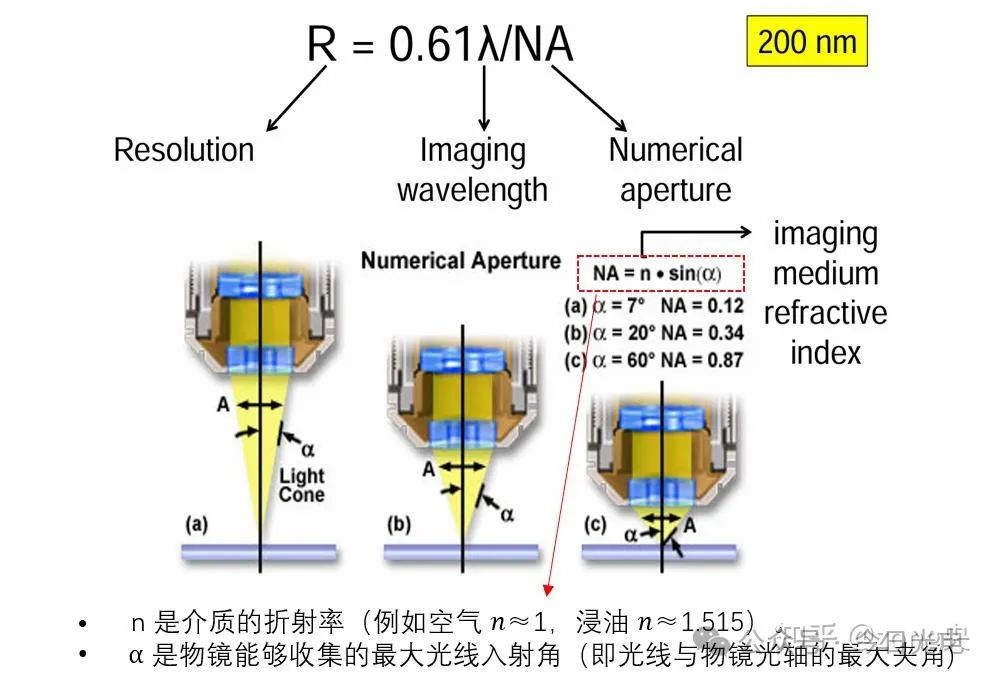
可以看到，和上面艾里斑半径公式的计算方式非常相似，只是引入了NA（数值孔径，Numerical aperture）的概念。

NA=n*sinα n和α的定义在图片已作出解释。

在实际成像中，如普通荧光显微镜，λ大小往往是固定的，而sinα最大也只能取到1，n最大也只能是1.7左右。

假设波长λ约为550纳米的绿光（GFP荧光），NA取1.7，代入公式，R的计算结果约为197nm。

改变参数后也仍在200nm左右, 这就是衍射极限数值的由来。

(其实还有一种计算显微镜的分辨率的方法是利用阿贝衍射公式：d= λ/2NA，虽然计算角度不同，但结果差别不大，在此不作细究)

当然上述分辨率极限说的只是普通的光学显微镜，电镜显微镜分辨率计算原理相似，主要是靠波长λ小。

那光学显微镜就永远卡在200nm分辨率了吗？

当然不。事实上，经过相关生物物理学家的进一步探索，已经出现了多种打破衍射极限的光学显微镜，即超分辨光学显微镜，如SIM，PALM, STORM, STED, MINFLUX等。我之后再一步步解释其原理。