单位增益带宽(UGB）-为什么一倍放大如此重要？

很多的运放都会单独的写什么单位增益稳定，我就在想为什么？平时放大都可能上百倍。为什么现在如此重要？

其实在很多应用中，运放常常工作在单位增益模式下（例如缓冲器、跟随器、增益为1的缓冲放大器等），在这些情况下，单位增益带宽提供了运放能够处理信号的最大频率范围。

很多运放，增益带宽积（Gain-Bandwidth Product, GBW）是一个固定值。因此，增益越高，带宽越小，反之亦然。单位增益带宽就是这种折衷关系中的一个“极限点”，它给出了增益为1时的最大可用带宽。

表示在增益为1时，系统能够稳定放大的最大频率范围。

因为不可能出现增益0.5倍这种情况。其实说的是极限频率。

1. A 是运算放大器的增益。
2. f 是增益为 A 时，系统的带宽。

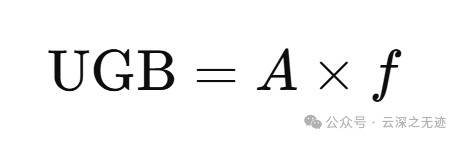
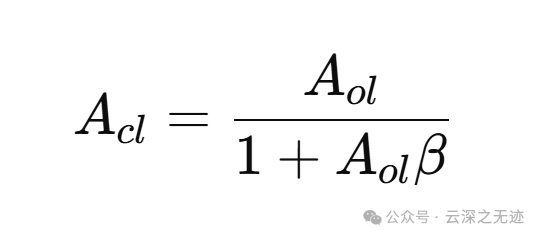
就是这样的一个公式，分类讨论一下就好了

当β=1 时：

1. 当反馈系数 β=1 时，运放的闭环增益达到单位增益（Acl=1）。这种情况下，运放的稳定性最差，因为此时系统没有额外的负反馈来降低增益带宽积（GBW），导致相位裕度（PM）较低，系统容易发生振荡。

2. 单位增益反馈会使得系统的增益带宽积限制到一个较小的值，因此系统的稳定性差，更容易受到噪声或高频信号的干扰。

当β<1 时：

1. 当闭环增益大于1时，β 会小于1（因为闭环增益与反馈系数 β 成反比），反馈变弱。此时，反馈对系统的控制作用减弱，系统的增益也会降低。

2. 增益带宽积（GBW）通常是固定的，因此，当闭环增益增大时，GBW会减小。随着GBW减小，系统的带宽变窄，相位裕度（PM）增大，从而增强了系统的稳定性。

这里出现了相位裕度，下篇文章说。不过总结一下上面：

1. 当闭环增益大于1时，由于增益变小，系统能够提供的带宽会增大，增益带宽积（GBW）相对降低。

2. 在闭环增益大于1时，虽然系统的带宽增大，但由于增益的降低，系统的稳定性提高，因为更低的增益通常会导致较高的相位裕度（PM），从而减少了振荡的风险。

可以看我下面的相位裕度的文章。

先记住相位裕度越大，系统越稳定，越不容易发生振荡。

增益较大时，相位裕度较小：当增益较大时，系统的反馈作用较强，但这可能导致相位裕度较小。相位裕度较小的系统容易发生振荡，尤其在高频时。也就是电容这种东西要少。

增益较小时，相位裕度较大：当闭环增益较小（即β\betaβ较小），系统的反馈作用减弱，相位裕度增大，系统变得更加稳定。

最后总结一下：

单位增益反馈 (
\beta = 1β=1)：系统的稳定性最差，因为增益和带宽受限，且相位裕度较低。此时，系统容易发生振荡。

闭环增益大于1时，β<1：系统的反馈变弱，增益带宽积（GBW）减小，带宽增大，带宽增大，导致相位裕度（PM）增大，系统的稳定性增强。

高增益情况下，反馈强度较大，导致相位裕度较小，因此系统稳定性较差。