手把手教系列之快速傅立叶算法

欢迎加入技术交流QQ群（2000人）：电力电子技术与新能源 1105621549

电力电子技术与新能源论坛

www.21micro-grid.com

小编推荐值得一看的书单电力电子技术与新能源推荐书单

• 合肥工业大学-张兴-高等电力电子技术-风力发电

• 最经典MOS管电路工作原理及详解没有之一

• SiC Power Module Packaging Design High Electrical and Therma

• [视频]逆变器Inverters, How do they work

• 光伏并网逆变器及其关键技术研究—张兴

  
  

• 功率逆变器Power Inverters Explained

• [刘进军]Modular Multilevel Converter for Medium-Voltage Motor Drive

• [视频]三相并网逆变器DQ控制

• [视频]阮新波_LCL并网逆变器电容电流全前馈抑制电网谐波

• 第五节 浙大反激电源设计指南

直接谈FFT，可能没这方面基础的同学，不太能明白，先看看它的相近较容易理解的几个概念吧。

啥是傅立叶级数？

在数学中，傅里叶级数（Fourier series）是把类似波的函数表示成简单正弦波的方式。更正式地说法是，它能将任何周期性函数或周期信号分解成一个（可能由无穷个元素组成的）简单振荡函数的集合，即正弦函数和余弦函数（或者，等价地使用复指数），从数学的定义来看，是这样地：

设x(t)是一周期信号,其周期为T。若x(t)在一个周期的能量是有限的，有即

则，可以将x(t)展开为傅立叶级数。怎么展开呢？计算如下：

公式中的k表示第k次谐波，这是个什么概念呢？不容易理解，看下对于一个方波的前4次谐波合成动图就比较好理解了。这里的合成的概念是时域上的叠加的概念，图片来源wikipedia

啥是傅里叶变换？

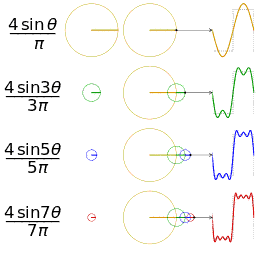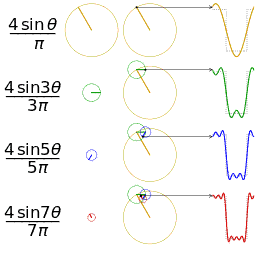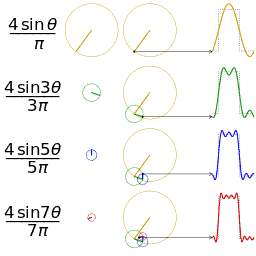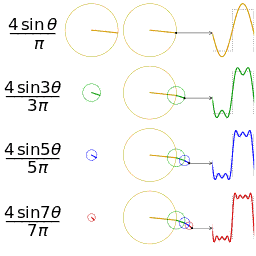
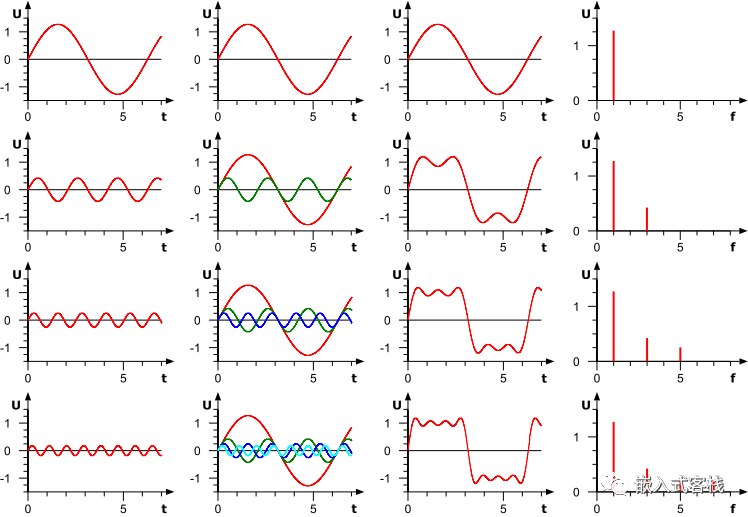
在数学中，傅里叶变换(Fourier transform FT )是一种数学变换，它将一个函数(通常是一个时间的函数，或一个信号)分解成它的组成频率，例如用组成音符的音量和频率表示一个音乐和弦。傅里叶变换指的是频域表示和将频域表示与时间函数相关联的数学运算。其本质是一种线性积分变换，用于信号在时域（或空域）和频域之间的变换，在物理学和工程学中有许多应用。因其基本思想首先由法国学者约瑟夫·傅里叶系统地提出，所以以其名字来命名以示纪念。实际上傅里叶变换就像化学分析，确定物质的基本成分；信号来自自然界，也可对其进行分析，确定其基本频率成分。其数学定义为：

对于连续时间信号x(t)，若x(t)在时间维度上可积分，（实际上并不一定是时间t维度，这里可以是任意维度，只需在对应维度空间可积分即可），即：

那么，x(t)的傅立叶变换存在，且其计算式为：

其反变换为：

上面这两个公式是啥意思呢？在度量空间可积可以理解成其在度量空间能量有限，也即对其自变量积分（相当于求面积)是一个确定值，那么这样的函数或者信号就可以进行傅立叶变换展开，展开得到的 就变成是频域的函数了，如果对频率 将函数值绘制出曲线就是我们所说的频谱图，而其反变换就比较好理解了，如果我们知道一个信号或者函数谱密度函数 ，就可以对应还原出其时域的函数，也能绘制出时域的波形图。

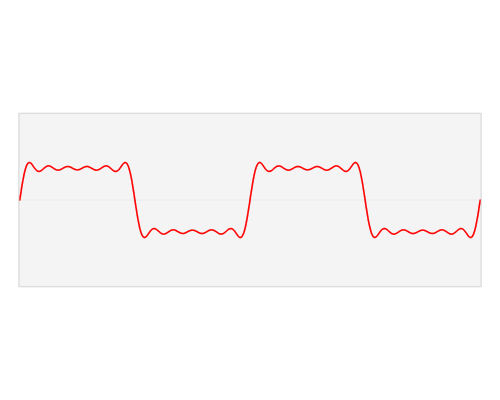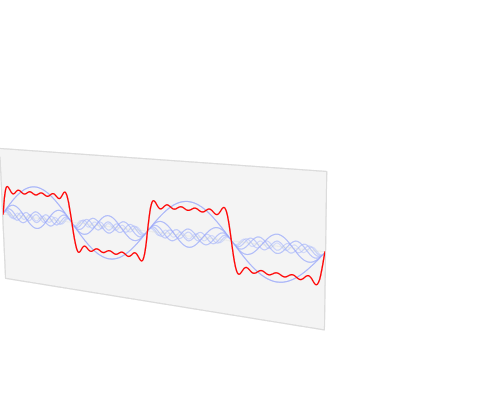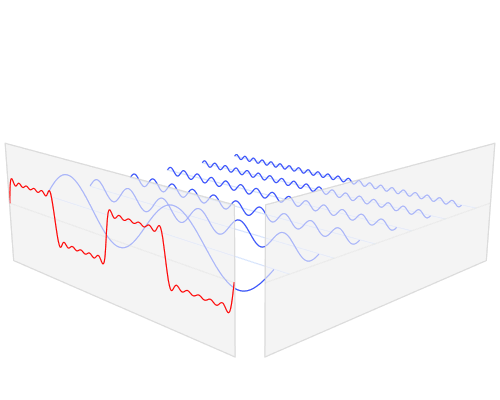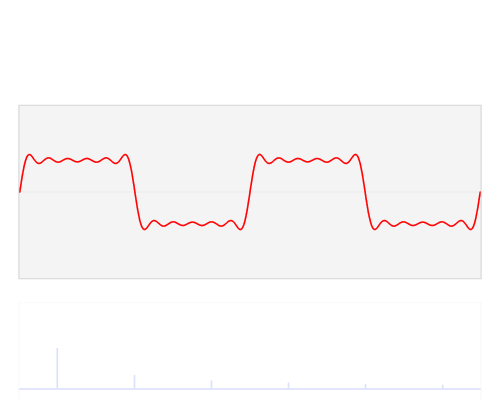
当然，本文限定讨论时域信号是因为我们电子系统中的应用最为普遍的就是一个时域信号，当然推而广之，其他的多维度信号也能利用上面定义进行推广，同样在多维空间信号也非常有应用价值，比如2维图像处理等等。

上面两个概念是一个东东么？

• 傅立叶级数对应的是周期信号，而傅立叶变换则对应的是一个时间连续可积信号（不一定是周期信号）
• 傅立叶级数要求信号在一个周期内能量有限，而后者则要求在整个区间能量有限
• 傅立叶级数的对应 是离散的，而傅立叶变换则对应 是连续的。

故而，两者的物理含义不同，且其量纲也是不同的， 代表周期信号的第k次谐波幅度的大小，而 则是频谱密度的概念。所以答案是这两者从本质上不是一个概念，傅立叶级数是周期信号的另一种时域的表达方式,也就是正交级数,它是不同的频率的波形的时域叠加。而傅立叶变换则是完全的频域分析，傅里叶级数适用于对周期性现象做数学上的分析，傅里叶变换可以看作傅里叶级数的极限形式，也可以看作是对周期现象进行数学上的分析，同时也适用于非周期性现象的分析。傅里叶级数适用于对周期性现象做数学上的分析，傅里叶变换可以看作傅里叶级数的极限形式，也可以看作是对周期现象进行数学上的分析，同时也适用于非周期性现象的分析。

啥是离散傅立叶变换？

离散傅里叶变换（Discrete Fourier Transform，缩写为DFT），是傅里叶变换在时域和频域上都呈离散的形式，将信号的时域采样变换为其DTFT的频域采样。

在形式上，变换两端（时域和频域上）的序列是有限长的，而实际上这两组序列都应当被认为是离散周期信号的主值序列。即使对有限长的离散信号作DFT，也应当将其看作其周期延拓的变换。在实际应用中通常采用快速傅里叶变换计算DFT。

对于N点序列 ,它的离散傅立叶变换为(DFT)为：

其中k=0,1,....,N-1,上面的式子展开一下：

啥是快速傅立叶变换？

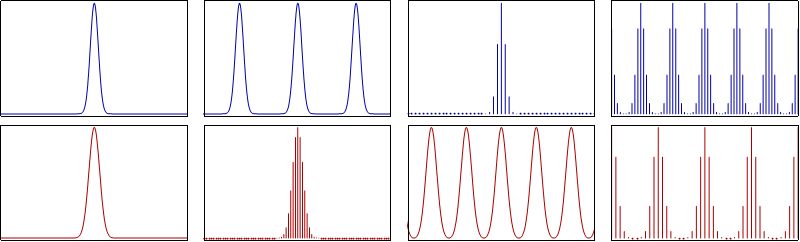
快速傅立叶变换（Fast Fourier Transform：FFT）是一种计算数字信号序列的离散傅立叶变换（Discrete Fourier Transform：DFT）或其逆变换（IDFT）的算法。傅里叶分析将信号从其原始域(通常是时间或空间)转换为频域的表示，反之亦然。DFT是通过将一系列值分解成不同频率的分量来获得的。这个操作在很多领域中都很有用，但是直接从定义中计算它通常太慢而不实际。FFT通过将DFT矩阵分解成稀疏(大部分为零)因子的乘积来快速计算这种转换。所以其本质是实现离散傅立叶变换的一种优化算法，将时间复杂度从 降低为 ,其中N为待计算序列的长度。当N非常大时，这种优化在时间维度上提升是非常显著的。尤其在嵌入式应用领域，由于受限于采用的芯片算力往往不强，所以FFT算法较之于DFT的效果是非常有应用价值的。

1994年，Gilbert Strang将FFT描述为“我们一生中最重要的数值算法”，并被IEEE杂志《计算科学与工程》列入20世纪十大算法之一，它深远的影响了我们世界与日常生活。说这个算法改变了世界也不为过。在我们日常生活中很多设备里面都有它的影子，比如手机、比如photoshop，比如数字音响等等。

快速傅立叶算法的最核心思想就是计算机科学里面常见的分治思想，即把一个复杂的问题，分解为一个小的类似问题进行求解。

FFT基本上可分为两类，时间抽取法和频率抽取法，而一般的时间抽取法和频率抽取法只能处理长度N=2M的情况，另外还有组合数基四FFT来处理一般长度的FFT。所谓抽取，就是把长序列分为短序列的过程，可在时域也可在频域进行。最常用的时域抽选方法是按奇偶将长序列不断地变为短序列，结果使输入序列为倒序，输出序列为顺序排列，这就是Coolly—Tukey算法。

假定待变换离散时间序列信号长度为 ，将x(n)按照奇偶分组：

上式可变换为：

令

其中，k取0，1，...，N/2-1

从而，

由于A(k),B(k)都是 点的DFT，X(k)为N点的DFT。那么这一分治思想还可以进一步做下去，这里就不赘述了。

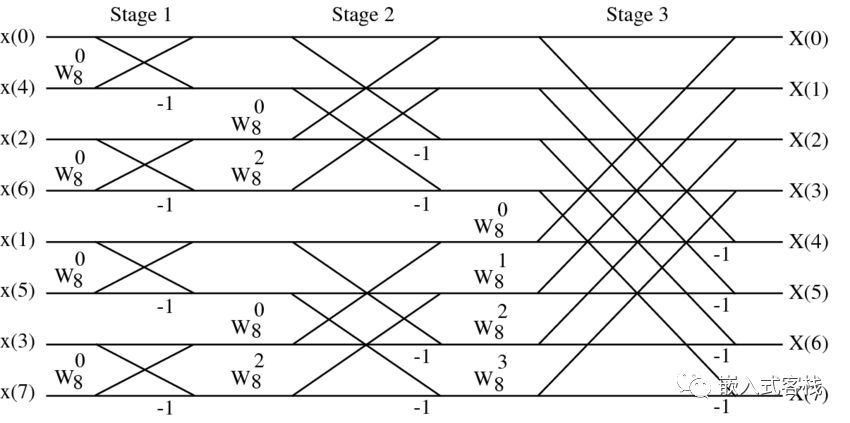
下图就是一个时间抽取的基2FFT算法的示意图：

对于频率抽取基2的示意图其原理类似，这里放个图：

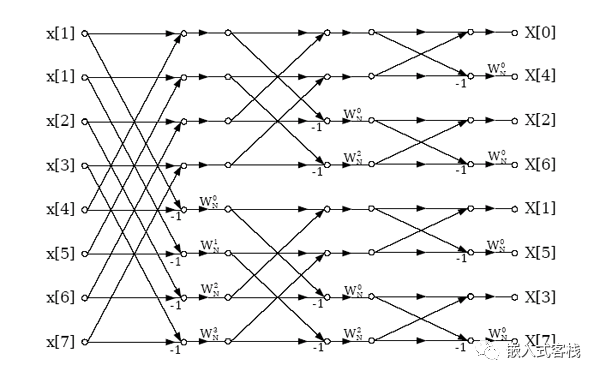
不同点：

• DIT2 FFT是在时域先进行奇欧倒序，频域输出为正序
• DIF2 FFT其输入序列在时域是正序，而频域输出为奇偶分开的倒序。

代码实践

好了，前面码了这么多字，还是不够直观，为了更好说明前面的分治思想，这里放了个递归实现代码测一下看看疗效：

#include <assert.h>
#include <math.h>
#include <stdio.h>
#include <stdlib.h>

#define q 8      /* 2^q 点，256 */
#define N (1<<q)  /* N点 FFT, iFFT */

typedef float real;
typedef struct{
  real Re; 
  real Im;
} complex;

#ifndef PI
# define PI 3.14159265358979323846264338327950288
#endif

/*为了更好说明分治思想，这里采用递归实现，结束条件为N<=1*/
void fft( complex *v, int n, complex *tmp )
{
  if(n>1) {   /* N如小于1，直接返回*/
    int k,m;    complex z, w, *vo, *ve;
    ve = tmp; vo = tmp+n/2;
    for(k=0; k<n/2; k++) {
      ve[k] = v[2*k];
      vo[k] = v[2*k+1];
    }
    fft( ve, n/2, v );  /* FFT 偶数序列 v[] */
    fft( vo, n/2, v );  /* FFT 偶数序列 v[] */
    for(m=0; m<n/2; m++) {
      w.Re = cos(2*PI*m/(double)n);
      w.Im = -sin(2*PI*m/(double)n);
      z.Re = w.Re*vo[m].Re - w.Im*vo[m].Im; /* Re(w*vo[m]) */
      z.Im = w.Re*vo[m].Im + w.Im*vo[m].Re; /* Im(w*vo[m]) */
      v[  m  ].Re = ve[m].Re + z.Re;
      v[  m  ].Im = ve[m].Im + z.Im;
      v[m+n/2].Re = ve[m].Re - z.Re;
      v[m+n/2].Im = ve[m].Im - z.Im;
    }
  }
  return;
}

/*为了更好说明分治思想，这里采用递归实现，结束条件为N<=1*/
void ifft( complex *v, int n, complex *tmp )
{
  if(n>1) {   
    int k,m;    complex z, w, *vo, *ve;
    ve = tmp; vo = tmp+n/2;
    for(k=0; k<n/2; k++) {
      ve[k] = v[2*k];
      vo[k] = v[2*k+1];
    }
    ifft( ve, n/2, v );  /* FFT 偶数序列 v[] */
    ifft( vo, n/2, v );  /* FFT 奇数序列 v[] */
    for(m=0; m<n/2; m++) {
      w.Re = cos(2*PI*m/(double)n);
      w.Im = sin(2*PI*m/(double)n);
      z.Re = w.Re*vo[m].Re - w.Im*vo[m].Im; /* Re(w*vo[m]) */
      z.Im = w.Re*vo[m].Im + w.Im*vo[m].Re; /* Im(w*vo[m]) */
      v[  m  ].Re = ve[m].Re + z.Re;
      v[  m  ].Im = ve[m].Im + z.Im;
      v[m+n/2].Re = ve[m].Re - z.Re;
      v[m+n/2].Im = ve[m].Im - z.Im;
    }
  }
  return;
}

#define SAMPLE_RATE (10000.0f)
int main(void)
{
  complex v[N], scratch[N];
  float amp[N];
  int k;

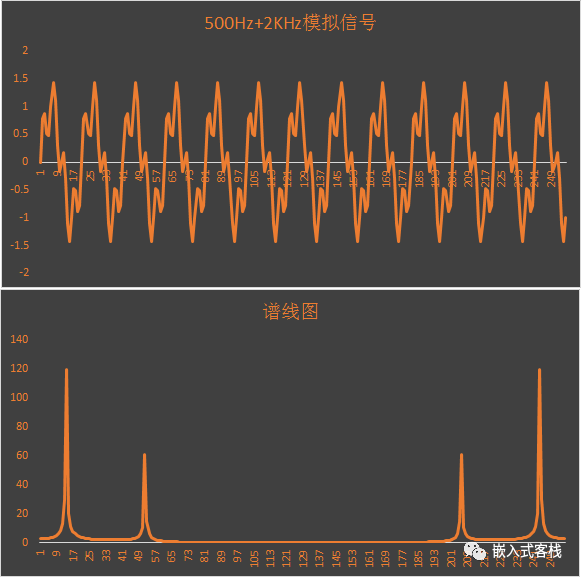
  /*模拟一个采样系统，采样率为10KHz，有两个信号：500Hz/2kHz*/
  for(k=0; k<N; k++) {
    v[k].Re = 1*sin(2*PI*500*k/SAMPLE_RATE)+0.5*sin(2*PI*2000*k/SAMPLE_RATE);
    v[k].Im = 0;//实际信号处理时，虚部常为0
  }
    
  /*输出模拟信号*/
  for(int i=0;i<N;i++)
  {
      printf("%f,",v[i].Re);      
  }
  printf("\n");  
  fft( v, N, scratch );

  for( int i=0;i<N;i++)
  {
      printf("%f,",sqrt(v[i].Re*v[i].Re+v[i].Im*v[i].Im));
  }
  printf("\n");  
  while(1);
}

代码来源：https://www.math.wustl.edu/~victor/mfmm/fourier/fft.c

为华盛顿大学的教学代码，上面代码仅测试了正变换，对于逆变换有兴趣的可以试试。

总结一下

本文目的为了方便理解快速傅立叶的算法思想，如果需要将算法实际应用到单片机或者DSP中，还需要做进一步的优化，实际使用时，一般会将蝶形算子做成一个表，另外也会做定点优化。对于ARM芯片而言，其CMSIS库有现成的实现例子可以直接使用，对于TI系列DSP而言，也内置了FFT代码库，可直接使用。