
高光谱成像的应用范围涵盖从医学诊断到农作物监测。然而,传统的扫描式高光谱成像仪速度慢、价格昂贵、难以广泛应用。快照技术通常局限于笨重的台式结构或较低的空间光谱分辨率。美国研究团队提出了一种紧凑、廉价的快照高光谱计算相机。该系统由直接放置在图像传感器上的平铺光谱滤波器阵列和放置在传感器附近的散射片组成。每个映射到光谱滤波阵列上的物点存在唯一模式,该模式编码多路空间光谱信息。通过求解稀疏约束逆问题,能够实现以亚像素超分辨恢复高光谱体。相关研究成果以“Spectral DiffuserCam: lensless snapshot hyperspectral imaging with a spectral filter array”为题,发表于Optica期刊。
高光谱成像系统旨在捕获包含每个空间位置光谱信息的三维空间光谱立方体。这使得通过光谱指纹能够检测和分类不同材料属性。传统的高光谱成像仪依赖于光谱滤波器或线扫描装置扫描高光谱立方体。这些方法成像速度慢,且通常需要精确的位移部件,增加了相机的复杂性。一些快照方法通过使用彩色滤光片阵列或拆分相机的视场来提高空间分辨率。计算成像方法可以通过对入射光进行空间光谱编码,然后解决压缩感知逆问题来恢复光谱立方体。然而这些系统通常带有笨重的继电器透镜、棱镜或衍射元件,并不适用于实际应用。
研究团队提出了一种新的编码方案,该方案利用图像化薄膜光谱滤波器以小尺寸实现高分辨率快照高光谱成像。实验系统由直接放置在传感器上的平铺光谱滤波器阵列和放置在距离传感器一段距离的随机相位掩模(即散射片)组成。散射片在空间上复用入射光,每个空间点映射到相机上多个像素。光谱滤光器阵列通过结构化消除功能对入射光进行光谱编码。散射片的多路复用效果允许从传感器像素的子集中恢复场景信息,从而能够恢复完整的空间光谱立方体,且不会因使用非多路复用光学器件而导致分辨率损失。该系统可以解耦光谱和空间响应,从而实现高自由度设计。在给定场景稀疏性和散射片随机性的条件下,光谱采样由光谱滤波器决定,空间分辨率由散射片响应的自相关决定。
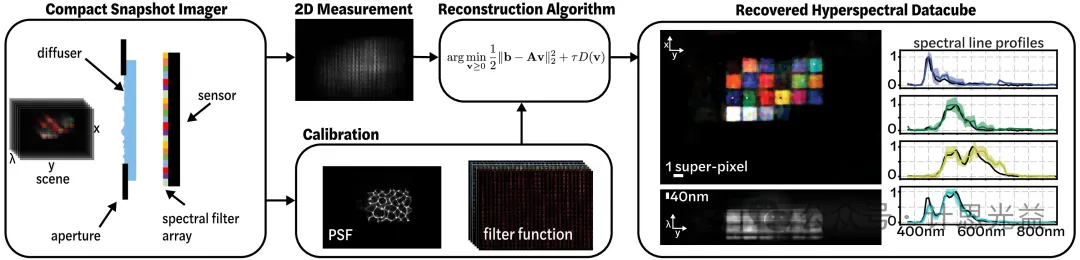
图1 光谱散射相机结构
文章研究了三种系统架构:一种是高数值孔径透镜,其衍射光斑尺寸与滤波器像素尺寸相匹配;一种是低数值孔径透镜,其衍射光斑尺寸与超像素尺寸相匹配;最后一种是将散射片作为多路复用光学器件。在高数值孔径透镜的情况下,场景中的点光源成像到传感器的单个滤波器像素上,因此只有当它在该滤波器的通带内时才会被测量,否则不记录。在低数值孔径透镜情况下,每个点源将被成像到滤波阵列超像素大小的区域,从而被传感器记录,但代价是低空间分辨率。散射片将每个点光源的光进行多路复用,使其经过多个滤光器像素,从而覆盖所有光谱带。在满足压缩感知条件的情况下,最终图像的空间分辨率可以达到相机像素大小的数量级。在实验中,系统空间分辨率将受到点扩散函数自相关的限制,即散射片点扩散函数必须跨越多个超像素,以确保捕获每个点。
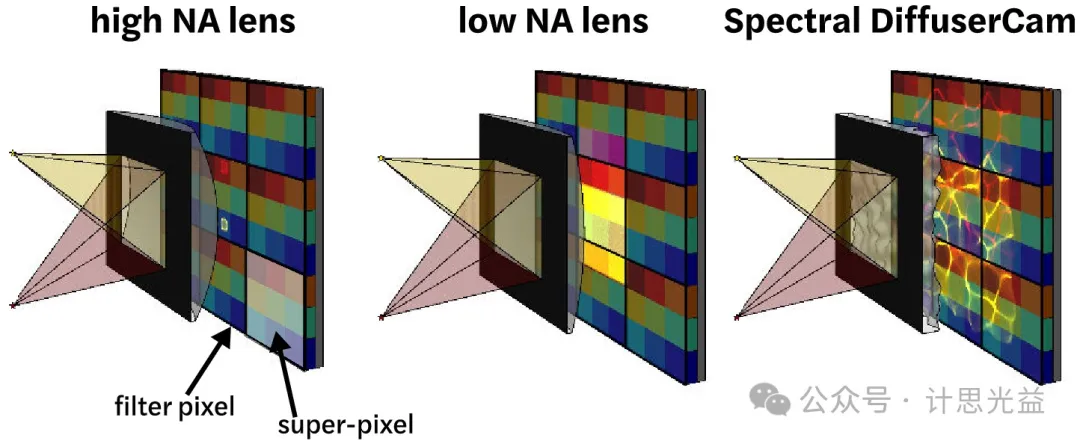
图2 三种系统框架对比
为了从二维测量中恢复高光谱数据,必须解决欠定逆问题。由于系统属于非相干、多路测量的压缩感知框架,因此采用L1范数最小化,在场景上使用加权3D全变分先验、频谱非负性约束以及低秩先验。实验构建了一个原型系统,散射片放置在距离传感器1 cm的位置。传感器具有659×494像素,将其裁剪为448×320像素以匹配光谱滤波器阵列的尺寸。光谱滤波器阵列由28×20超像素网格组成,每个超像素具有8×8的滤波像素网格。每个滤波像素尺寸为20 µm,覆盖的传感器像素略大于4。调整每张图像的曝光时间,范围从1毫秒到13毫秒。使用Cornerstone 130 1/3 m电动单色仪校准滤波函数,单色仪在半高宽处创建一个宽度为5 nm的窄带源。同时从386 nm到898 nm,以8 nm的增量测量滤波器响应扫描源,结果如图3(b)所示。由于散射片相对光滑且特征较大,因此点扩散函数作为波长的函数保持相对恒定,如图3(a)所示。因此,只需要通过捕获单点源校准图像来校准单个波长。在实验设置中,由于滤波器阵列比传感器小,因此可以使用原始传感器的边缘来测量点扩散函数,通过移动点源扫描原始传感器区域上点扩散函数的不同部分并将子图像拼接在一起。
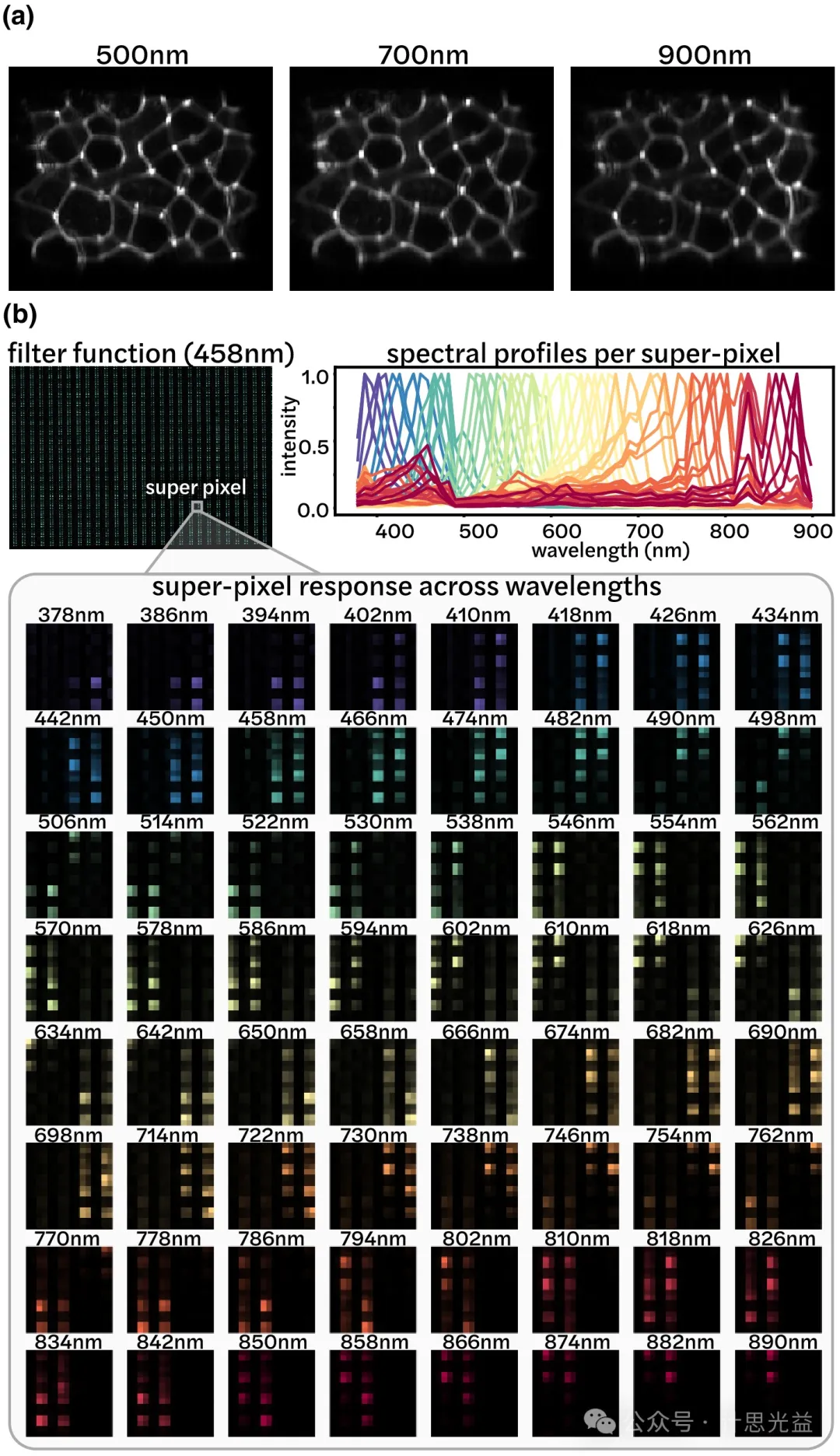
图3 光谱散射相机实验标定。(a)点扩散函数测量;(b)实测频谱滤波函数
结合实验系统参数,研究团队推导了系统理论分辨率,并用原型系统进行实验验证。由于该系统分辨率与场景相关,预计分辨率会随着场景复杂性的提高而降低。为了描述这一点,将系统与使用高数值孔径和低数值孔径透镜的系统进行比较。研究结果表明,在386-898 nm范围内的64个光谱通道中,两点空间分辨率约为0.19超像素,多点空间分辨率约为0.3超像素。图4显示了相互叠加的光谱重建采样,阴影块表示真值单色仪光谱。实验重建结果与真实波长5 nm范围内的真实峰值相匹配。
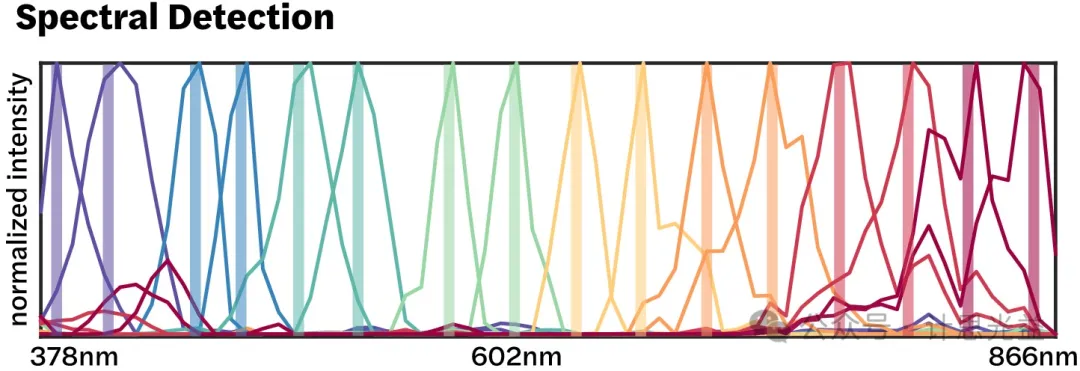
图4 光谱分辨率分析
由于图像重建算法包含非线性正则化项,两点分辨率测量不足以完全描述系统分辨率,因此,借助局部条件数分析将分辨率估计为对象复杂性函数。在已知支持下,局部状态数代表了正演模型的反转程度。在图5中,研究者计算了两种情况下的局部条件数,结果表明实验设计的散射片具有始终低于低数值孔径或高数值孔径透镜的状态数,对于大于0.3超像素的分离距离,状态数低于40。低数值孔径透镜需要接近1个超像素的分离距离,而高数值孔径透镜由于测量中的信息缺失而具有不稳定的状态数。
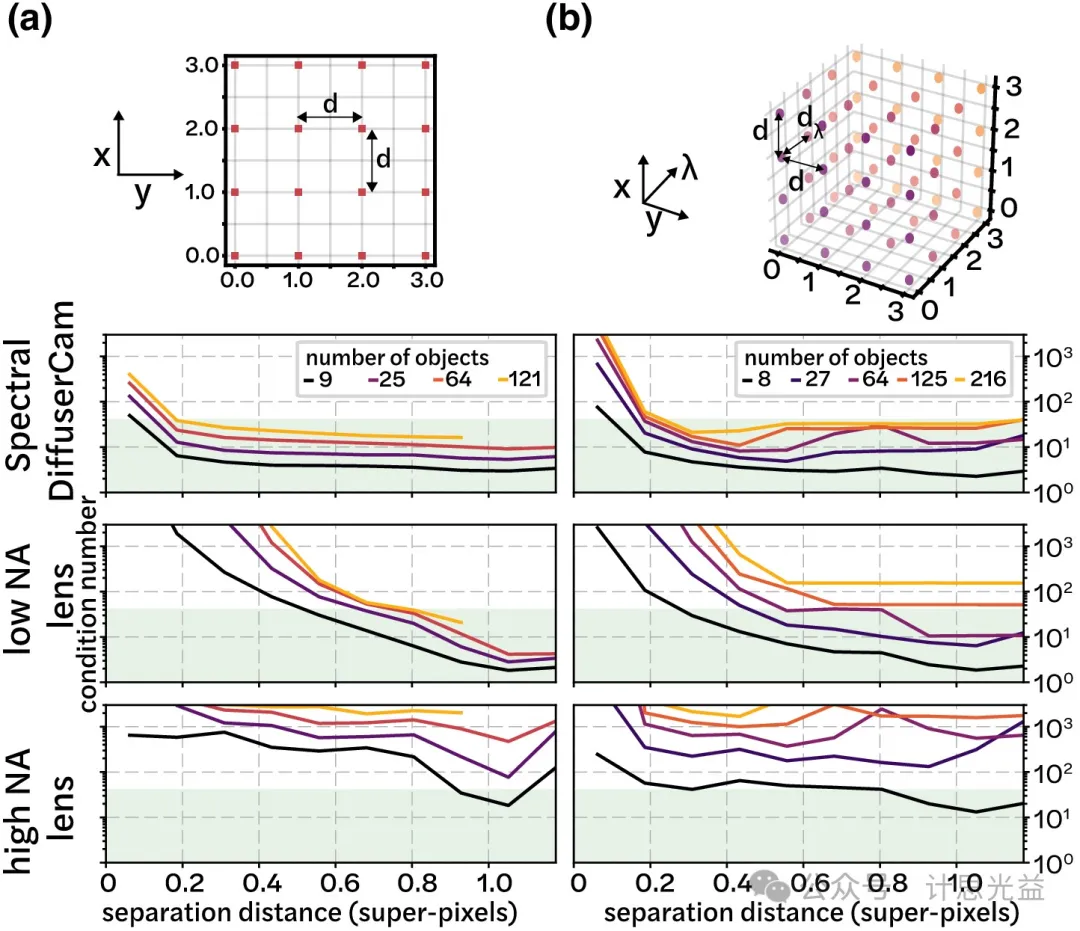
图5 光谱散射相机状态数分析。(a)理论分辨率;(b)实验重建分辨率
实验首先测量了USAF分辨率板和RGB LED网格,对于RGB LED场景,使用光谱仪测量LED的真值光谱曲线,恢复光谱曲线与真值匹配。接下来,研究团队展示了复杂物体的重建,其结果如图6所示。通过绘制由Thorlabs CCS200光谱仪从场景中四个点测量的真值谱线剖面图,结果表明文章方法可以准确地恢复光谱。每张图像都显示了一个参考RGB场景,表明重建在空间上与期望场景相匹配。
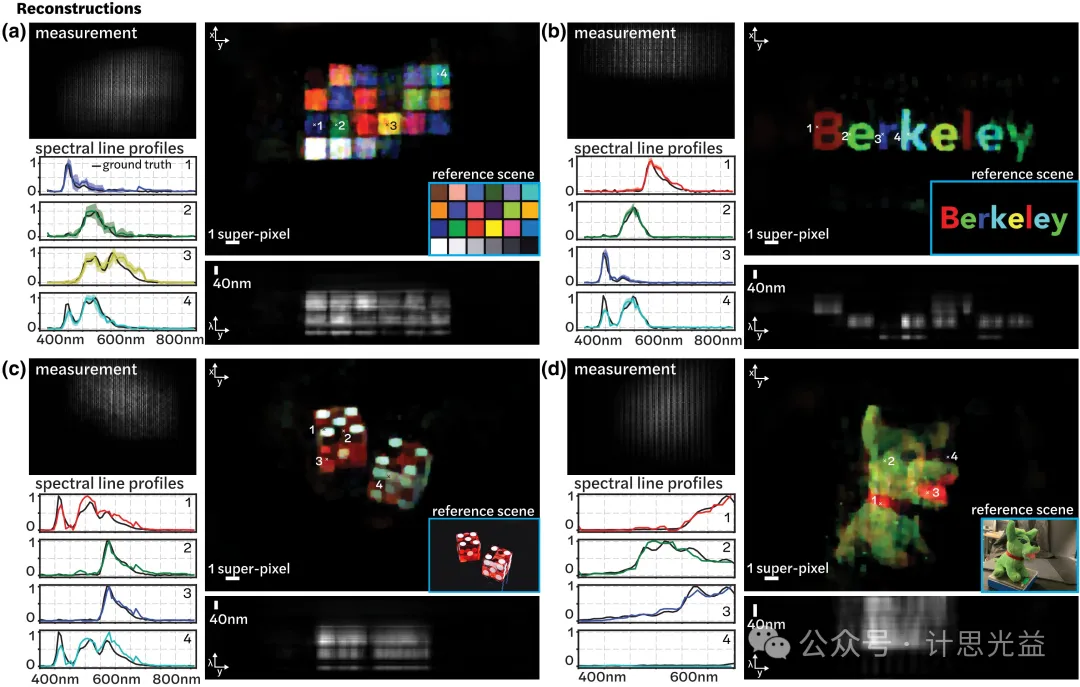
图6 高光谱重建实验结果
综上所述,该工作提出了一种新颖的高光谱成像方法,其结合了彩色滤光片阵列和无透镜成像技术,从而实现了紧凑廉价的高光谱相机。光谱滤波器阵列将光谱信息编码到传感器上,散射片对入射光进行多路复用,使得每个点映射到多个光谱滤波器。相机的多路复用特性使其能够使用压缩感知从单个2D测量中重建高空间分辨率光谱。研究者对相机的预期分辨率进行了分析,并对系统的两点和多点分辨率进行了实验表征。最后,构建了一个原型相机并展示了复杂空间光谱场景的重建,相机在64个光谱波段中实现了高达0.19超像素的空间分辨率。
原文链接:
https://doi.org/10.1364/OPTICA.397214

