求解四边形的面积

  前几天看到网络上这么几道中学趣味数学题，包括一个求取矩形内部多边形面积的问题。原以为可以通过瞪眼法秒解，但谁承想，脑回路烧冒烟了，还是没有得到一个简明求解思路。今天终于想出来了一个自认为满意的求解过程。就放在这里给未来思维能力日益减退的自己讲一讲。

二、求解过程

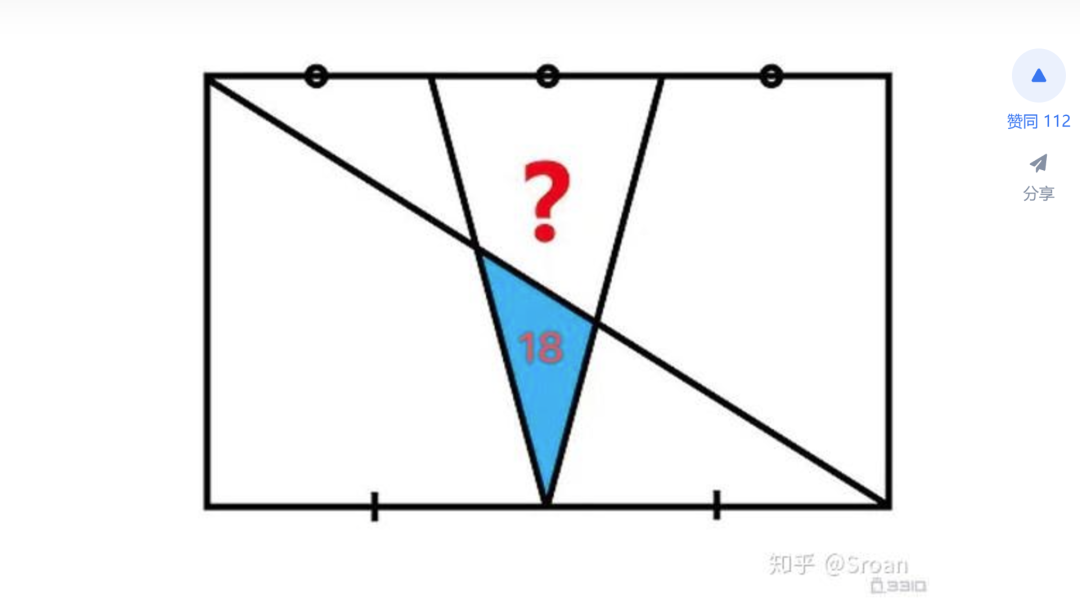
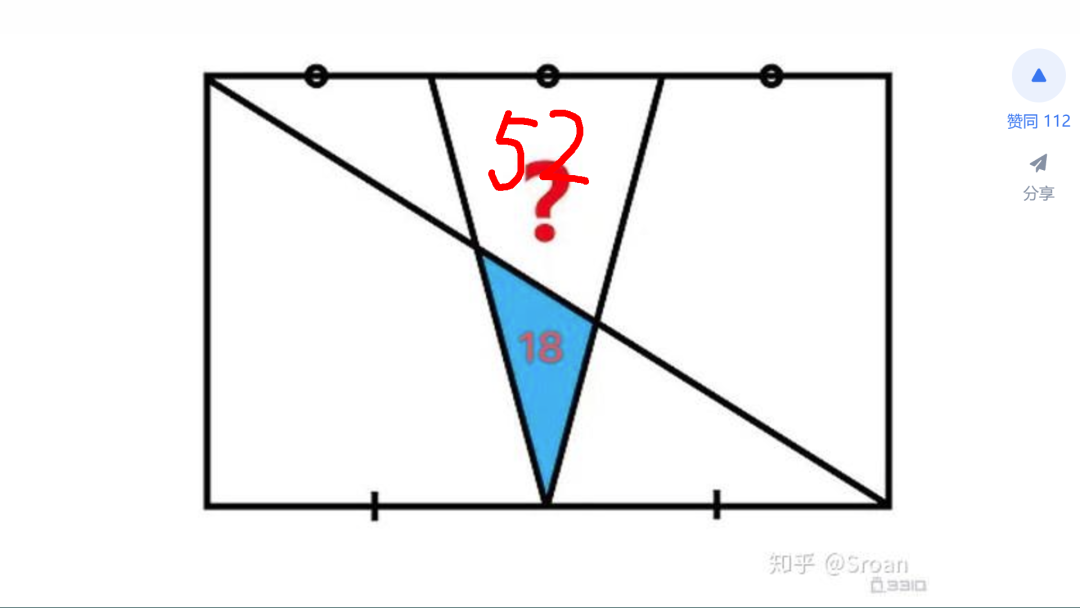
  问题本身比较简单。在一个比较平凡的矩形中，上边被均匀分成了六份，下面均匀分成了四份，后来才知道这个条件没有作用。中间稳稳当当的有一个漂亮的三角形，三角形的底边显然是平行四边形长度的三分之一，高度与四边形的高相同。被四边形对角线分割出来的下面这个小三角形面积为 18。求取上面这个四边形的面积。根据直观感觉，这个问题应变是有确定答案的。而且与长方形的长宽比值无关。

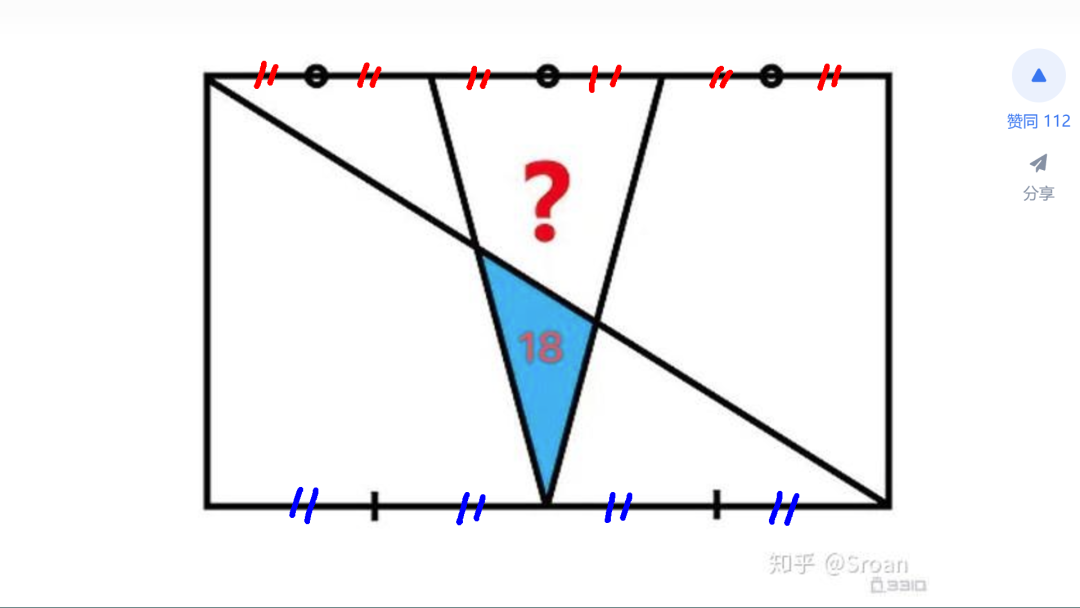
  开始的思路是化繁为简，将待求面积的四边形一分为二。上面相邻三角形，与已知面积的三角形等高，所以它与已知三角形的面积之比等于它们底边长度之比。这两个相邻三角形形成一个大的扩展三角形。接下来，另外一个三角形，与扩展后的三角形等高，同样，它的面积与扩展三角形面积的比值等于底边长度的比值。由此可见，如果两个斜边线段的比值可以求出，上面四边形的面积也就可以得到了。

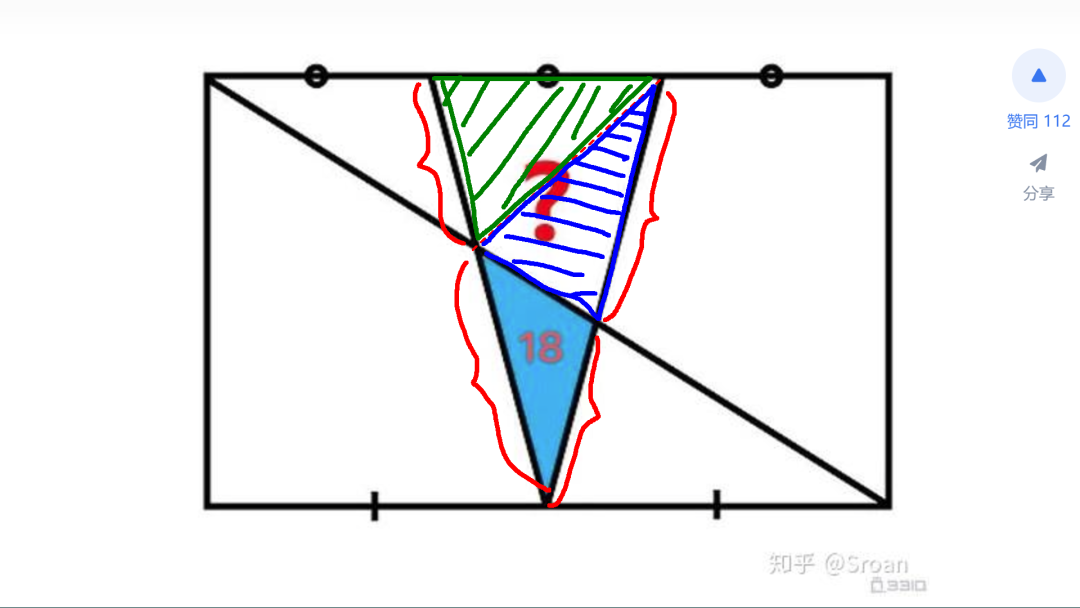
  对于右边斜边线段的比值，可以看到，它等于平行四边形斜边上两个线段的比值，这是因为上面和下面两个三角形是相似的。此处省略一百字。同样，左边斜边线段的比值，也等于对角线两个线段的比值。所以，只要知道对角线这三个线段的比值，就可以求出最终的答案。假设，四边形的对角线长度为 A，下面分别求取三条线段各占多少。

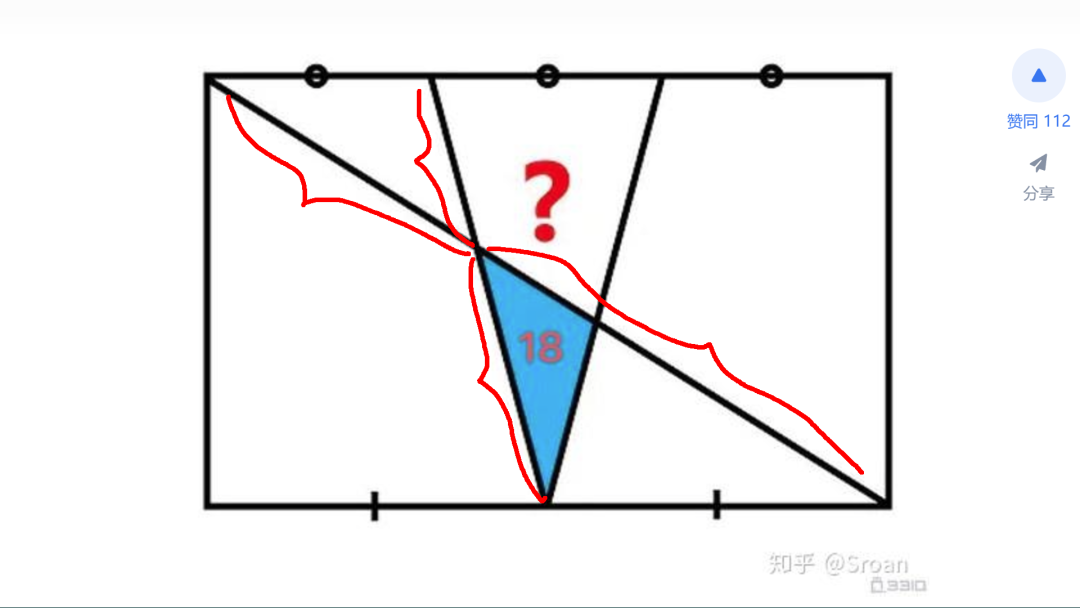
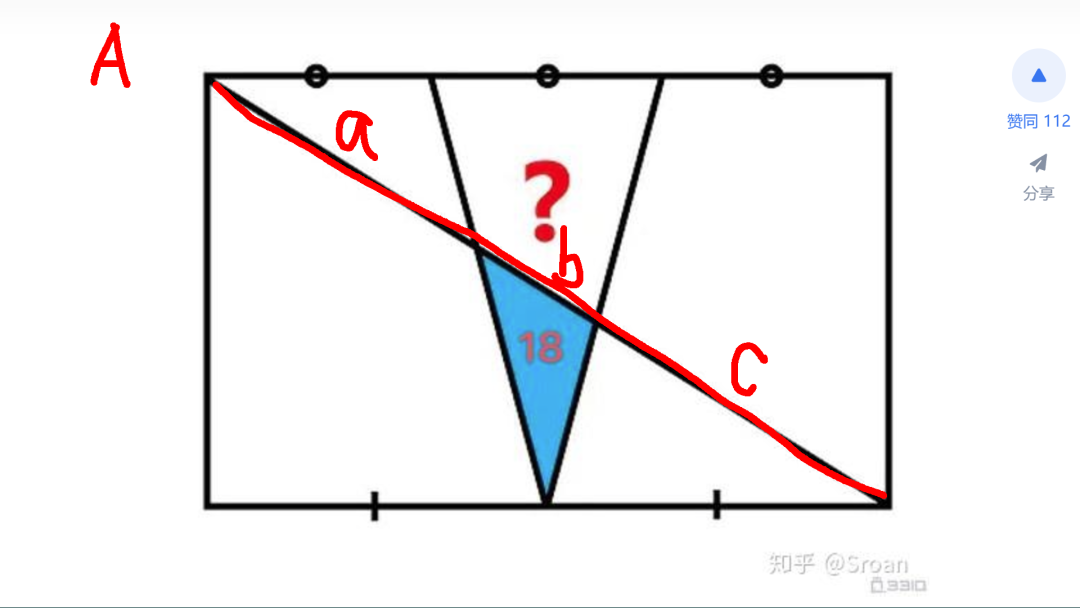
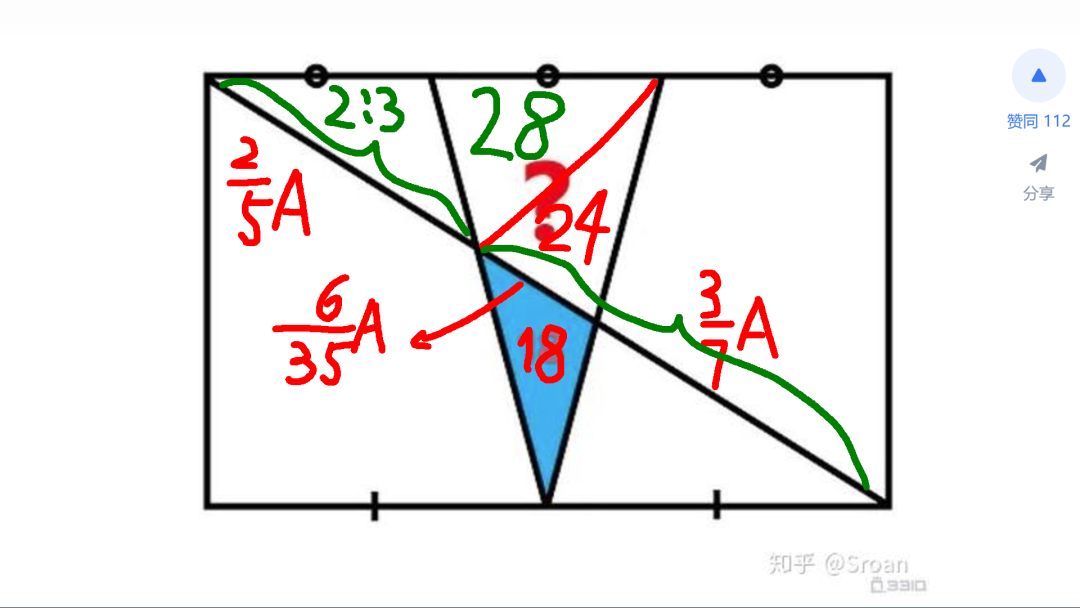
  下面利用三角形底边平行线比例分割斜边的性质求取对角线各线段的比值。对于右边斜边，在四边形外边补齐一个与其平行的斜边，与四边形下面的三角形合并成一个大的三角形。下面延长出来的底边长度等于平行四边形长度的六分之一。由此，下面两段长度的比值，等于对角线两段长度的比值。先求取下面线段的长度，分别是四边形长度的 2/3以及1/2。由此可以知道上面两段线段的比值为 3:4。所以，得到对角线下面线段长度为整个对角线长度的 3/7。

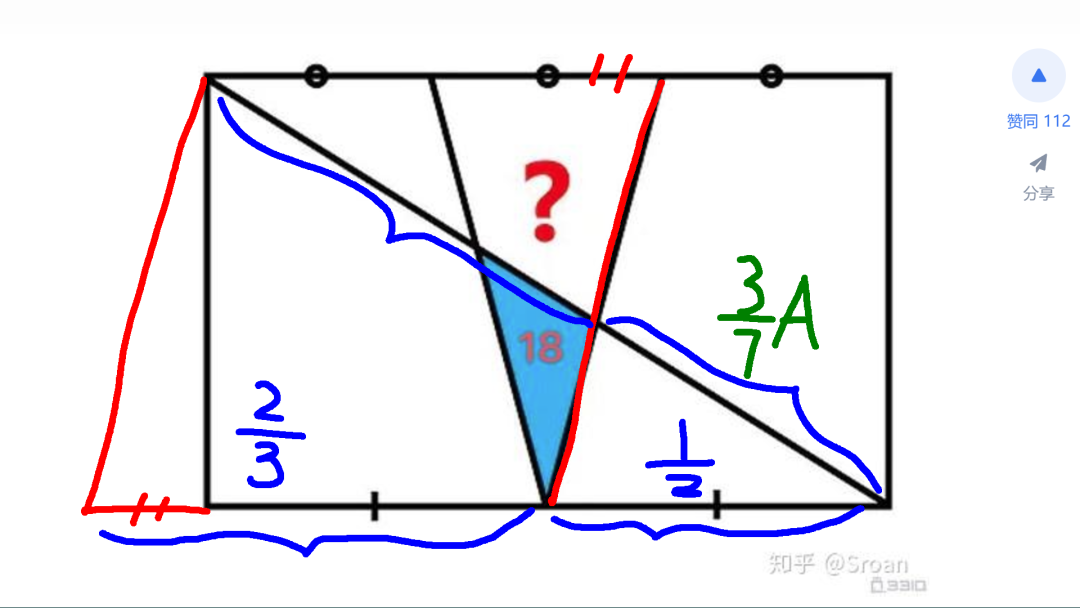
  利用同样的魔法，在四边形内部补齐平行于左边斜边的线段。上面两端的长度，分别是长方形长度的六分之二，和 六分之三。由此可以得到对角线上两段线段的长度比值，等于 2:3。这样，对角线上面线段长度等于总长度的 2/5。

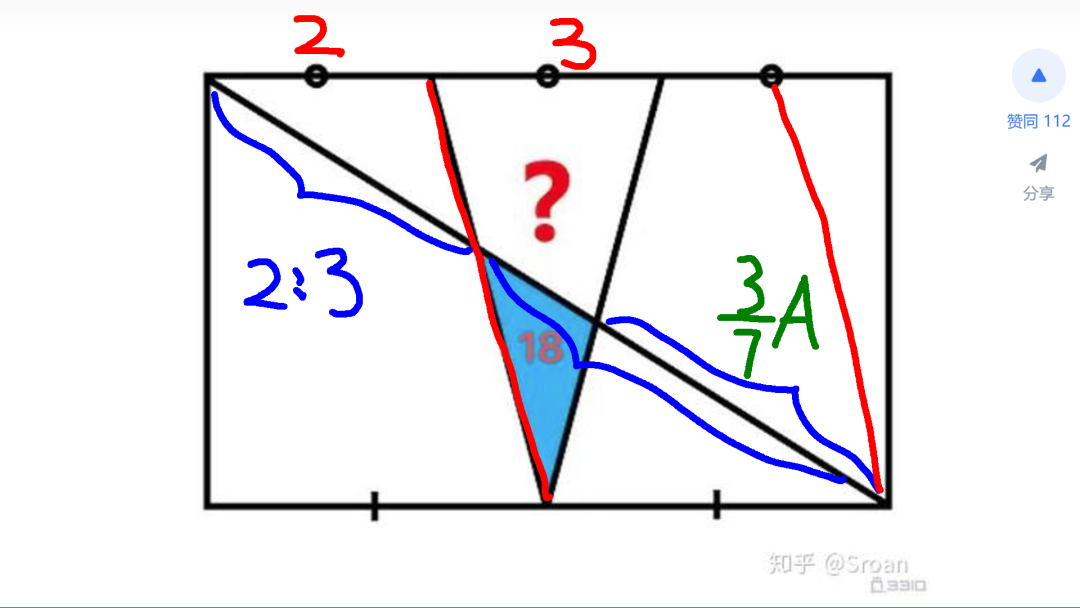
  对角线剩下中间线段的长度，也就可以求出，等于总长度的 6/35。

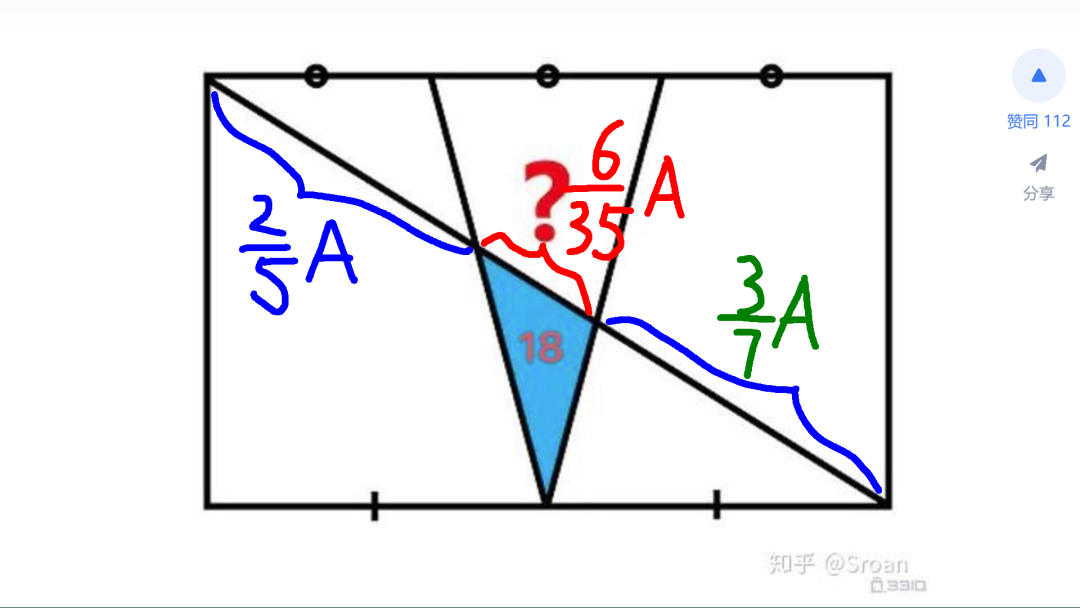
  接下来，根据刚才的结果，逐步求取四边形的面积。先求取相邻三角形的面积。它于已知三角形的面积之比，等于底边长度的比值。这个比值等于四边形对角线两个线段的比值。根据已知的长度，可以计算出这个比值为 4:3。因此，根据已知三角形面积，便可以求取上面三角形的面积为24。

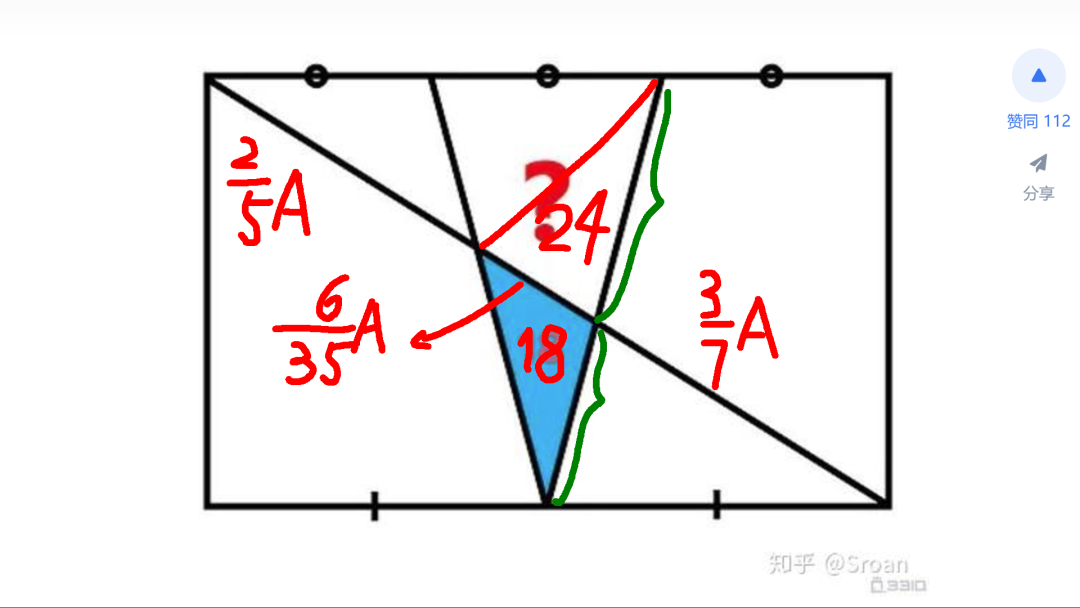
  接下来，对于上面三角形的面积，与下面扩展后三角形面积的比值，等于四边形对角线两个线段的比值。再根据已知对角线线段的长度，可以求取比值为 2:3。进而，根据扩展三角形的面积，便可以计算出上面三角形面积等与28。至此，上面四边形的面积便可以得到。等于两个三角形面积之和。最终数值为 52。

※ 总  结 ※

  好吧，让我的大脑降温一下。不知道你们是否有更加简洁的求取方法呢？