抽样函数（SamplingFunction）

抽样函数，也称为采样函数或Sinc函数，用于描述连续时间信号在离散时间点上的采样过程。

Sa(t) = sinc(t) = sin(πt) / (πt)

主瓣和旁瓣： sinc函数的主瓣在t=0处取得最大值1，随着t的增大，函数值逐渐衰减。主瓣两侧存在无限多个旁瓣，振幅逐渐减小。

零点： sinc函数在除了t=0以外的所有整数点上都为零。

偶函数： sinc函数是偶函数，即sinc(t) = sinc(-t)。

抽样定理告诉我们，如果一个连续时间信号的最高频率为f_m，那么为了不失真地恢复原信号，采样频率f_s至少要满足：

f_s >= 2f_m

这个最低采样频率称为奈奎斯特采样频率。

当一个连续时间信号x(t)被以采样频率f_s进行采样时，得到的离散时间信号x[n]可以表示为：

x[n] = x(nT)

其中，T是采样周期，T = 1/f_s。

而原连续时间信号x(t)可以用一系列的sinc函数的线性组合来表示，这就是著名的采样定理的数学表达形式。

sinc函数的傅里叶变换是一个矩形函数，因此sinc函数可以看作是一个理想的低通滤波器的冲激响应。

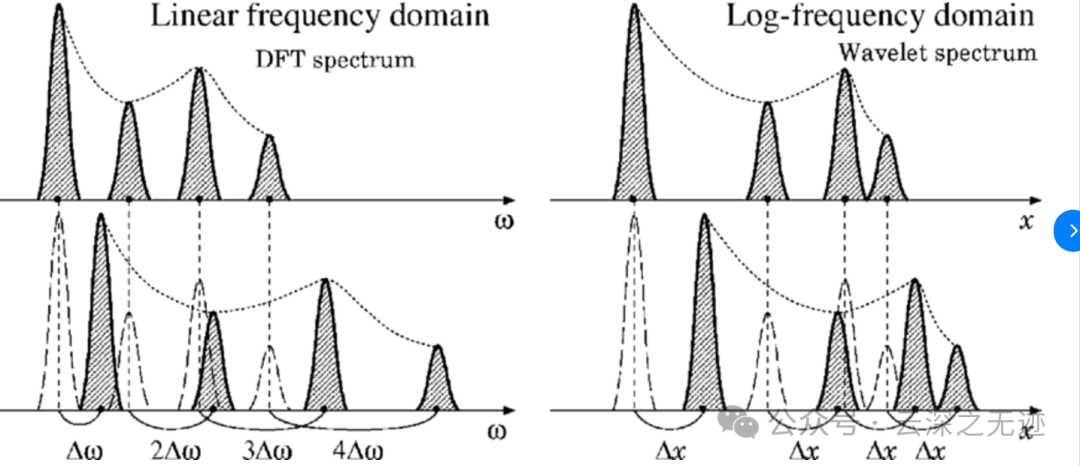
谱线间隔：

谱线间隔是指在频谱图上，相邻两个谱线之间的频率差。它反映了信号的周期性特征，是频谱分析中一个重要的参数。

基频，简单来说，就是一个周期性信号中频率最低（小）的成分。也是其他所有频率成分的整数倍。

1. 谱线间隔的倒数等于信号的周期。

2. 周期是信号重复出现的时间间隔。

   
   

频谱分辨率： 谱线间隔决定了频谱分析仪的分辨率，即能够分辨两个相近频率成分的能力。谱线间隔越小，分辨率越高。

谱线间隔，对于一个周期为T的信号，其基频f₀为：

f₀ = 1 / T

因此，谱线间隔也为f₀。

采样频率： 采样频率越高，得到的频谱分辨率越高，谱线间隔越小。

1. 正弦波信号： 正弦波信号的频谱只有一个谱线，谱线间隔等于信号的频率。

2. 方波信号： 方波信号的频谱是离散的，谱线间隔等于基频，且存在奇次谐波。