好像没写过,补一下:(这个主要在奎纳斯采样推导里面使用)
周期的就是和周期的傅里叶级数差不多

这个是算完的结果,可以看到这个是求和的符号
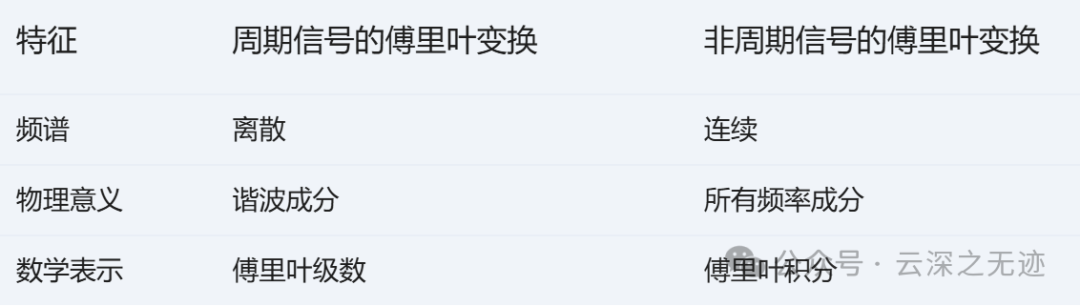
周期信号的傅里叶变换与非周期信号的傅里叶变换有着本质的区别。非周期信号的傅里叶变换得到的是一个连续的频谱,而周期信号的傅里叶变换则是一系列离散的频率成分。
周期性: 周期信号在时域上是重复的,这意味着它的频谱在频域上也是周期性的,并且只在特定的频率上存在非零值。
即只有在特定的频率点上才有幅值。这是因为周期信号可以表示为一系列谐波的叠加,而这些谐波的频率是基频的整数倍。
傅里叶级数: 周期信号可以表示为傅里叶级数,即一系列不同频率的谐波的线性组合。这些谐波的频率是基频的整数倍,频谱是离散的复指数函数。
对于一个周期为T的连续时间周期信号x(t),其傅里叶级数展开式为:
x(t) = Σ(n=-∞ to ∞) X[n] * e^(j*2π*n*t/T)X[n]是复傅里叶系数,表示频率为n*2π/T的谐波的复振幅。
周期信号的傅里叶变换可以看作是傅里叶级数的另一种表示形式。
频谱是离散的: 只有在频率为n*2π/T的整数倍处才有非零值。
频谱是周期性的: 频谱以2π/T为周期重复。
周期信号: 正弦波、方波等。它们的频谱是离散的,只有在基频及其谐波频率上有非零值。