连续时间非周期信号的傅里叶变换.罗里吧嗦版
非周期信号的傅里叶变换,这个在使用中更加的普遍,之前写过,好像有些过于拖沓了,这次快来复盘一下新的推导过程。
从物理概念上考虑,一个信号必然含有一定的能量,无论信号怎样分解,其所包含能量是不变的.所以不管周期增大至何种程度,频谱的分布依然存在.
或者从数学角度分析,极限情况下,无限多的无穷小量之和,仍可等于一个有限值,此有限值的大小取决于信号的能量.基于上述原因,非周期信号的频域分析不能采用先前的频谱表示法,于是人们引入了傅里叶变换来表示非周期信号的频谱分布.
从周期到非周期: 我们可以将非周期信号看作是周期无限大的周期信号。当周期趋近于无穷大时,傅里叶级数中的谱线逐渐稠密,最终形成连续的频谱,这就是傅里叶变换。
从离散到连续: 傅里叶级数的系数是离散的,而傅里叶变换的频谱是连续的。

得救之道就在其中!我终于把公式都学明白了!
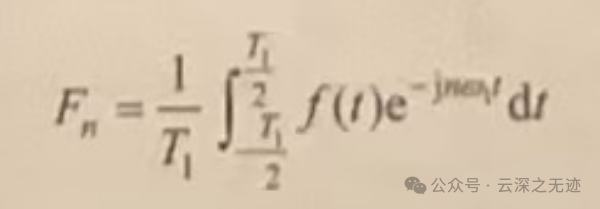
这就是是周期的系数计算式
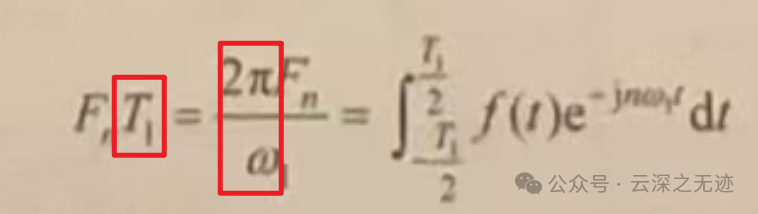
关键是这个,其实做了两个事情,把后面的周期1/T乘到了前面,接着就是把前面变换过的式子写了一次,使用2π/ω。
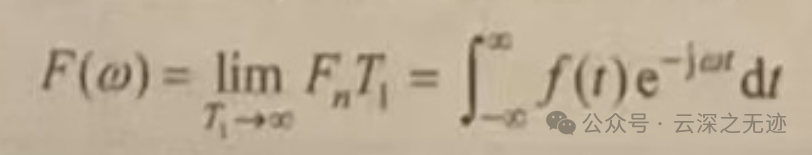
然后就是考虑这个T无限的时候怎么变换

上面的太模糊了,看这个吧,这个清晰,这里的FT被称为了新函数,其实我纠结这个乘法的本来意思,我使用了量纲分析以后,发现其实并没有什么物理上面的解释。
Fn 是一个复数,表示振幅和相位;T1 是时间,表示周期。二者物理量纲不同,直接相乘得到的量纲不明确。
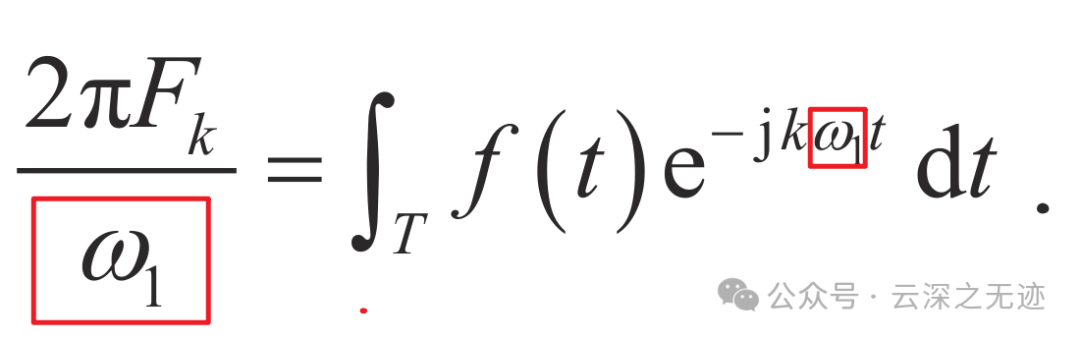
然后看这个,下面的ω趋于0
积分部分: 这部分是对函数f(t)乘以一个复指数函数后在整个周期内进行积分。这个复指数函数的作用是将时域信号投影到不同频率的基函数上,从而提取出不同频率成分的强度和相位。
复数 可以同时表示振幅和相位。
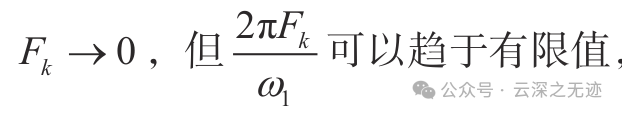
因为这里是非周期的,所以频谱系数是趋于0的,所以这一项变成了一个有限函数。重新定义一下:
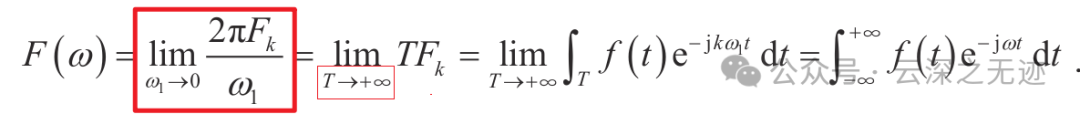
就出现了这个连等式
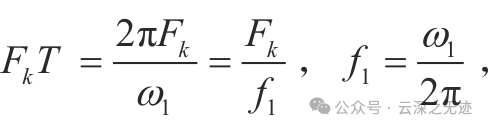
因为这个东西的成立,可以理解为单位频段内的谱系数,即频谱密度。
系数除以角频率就是单位角频率上面的密度,好了,这辈子忘不了。
F(ω)称为信号f(t)的频谱密度函数,它表示信号f(t)在不同频率ω处的频谱成分。
非周期信号:可以看作是由无数个不同频率的正弦波无穷小成分叠加而成,每个频率成分的振幅和相位由频谱密度函数F(ω)决定。
虽然到目前为止已经比较完美了,但是还是有点小遗憾。
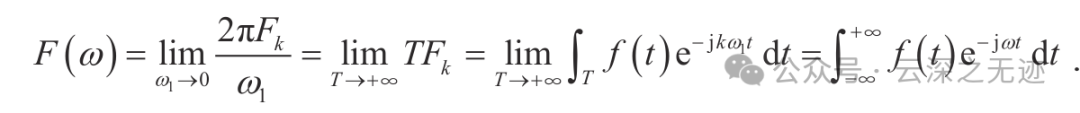
为什么在第一个等号后面它公式都趋于无穷了,为什么还能成为一个有限值。
为什么当周期T趋于无穷大时,傅里叶系数Fn虽然趋于0,但2π/T * Fn却可以趋于有限值,从而得到有限的傅里叶变换F(ω)。
周期无限大: 当周期T趋于无穷大时,非周期信号可以看作是周期无限大的周期信号。
频谱离散化: 对于周期信号,其频谱是离散的,即只有在特定的频率点上才有非零的傅里叶系数。
能量分散: 当周期无限大时,信号的能量在无限多的频率成分上分散,导致每个频率成分对应的傅里叶系数趋于0。
2π/T * Fn趋于有限值的原因
频谱密度: 2π/T可以看作是频率间隔,即相邻两个频率分量之间的距离。当T趋于无穷大时,这个频率间隔趋于0,频谱变得连续。
频谱密度函数: 为了描述连续频谱,引入了频谱密度函数F(ω),它表示单位频率内的频谱强度。
2π/T * Fn趋于有限值是因为引入了频谱密度的概念,将离散的频谱转化为连续的频谱,从而使得总能量保持不变。
有限能量: 虽然每个频率成分的强度趋于0,但当频率间隔趋于0时,这些无限多的、趋于0的强度叠加起来,却可以得到一个有限的总能量。
无论周期多大,信号的总能量是守恒的。当周期趋于无穷大时,能量只是在更密集的频率范围内分布。
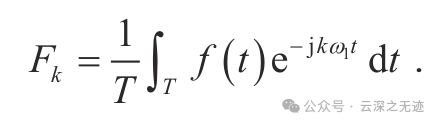
这个就是傅里叶的级数

这个就是最后的

当然了最后这个知识点也是要补充的