文章很短也很长，两类积分，在曲线和曲面上，四种类型，分别在标量和矢量情况下。三个定理，格林，高斯，斯托克斯。以及完整的微积分基本定理，在低维和高维之间互相连通。不管怎么说，会不会算，那是计算问题，如果不会区分，那是真没学会。
直线积分的自变量取值范围是直线，也就是实数轴，用 x 就可以指明自变量。而曲线积分的自变量取值范围是曲线，需要(x,y)才能指明自变量。
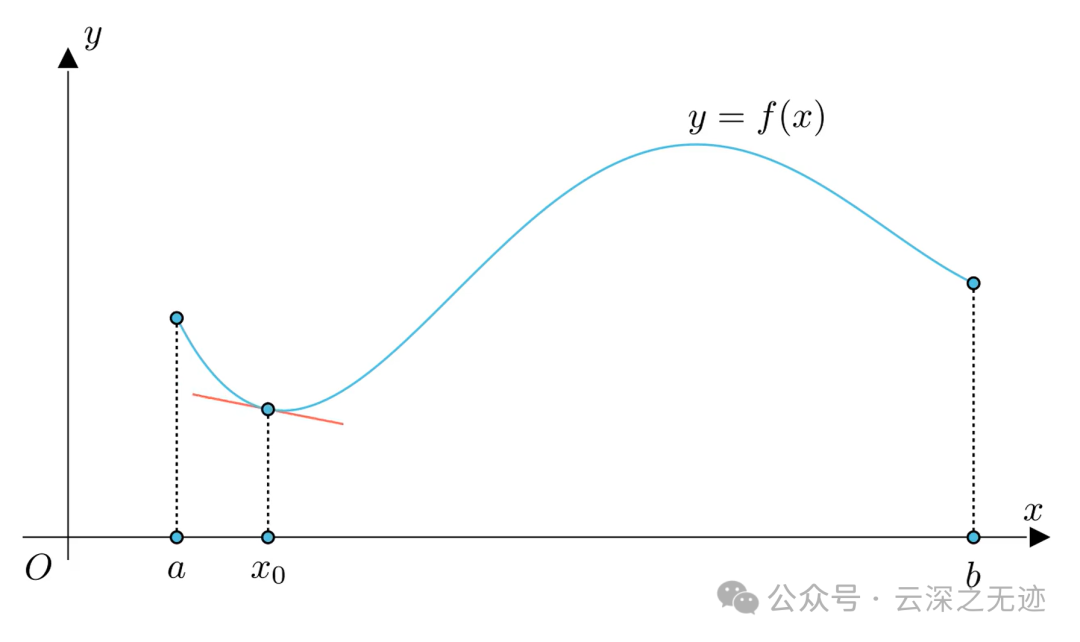
光滑曲线弧
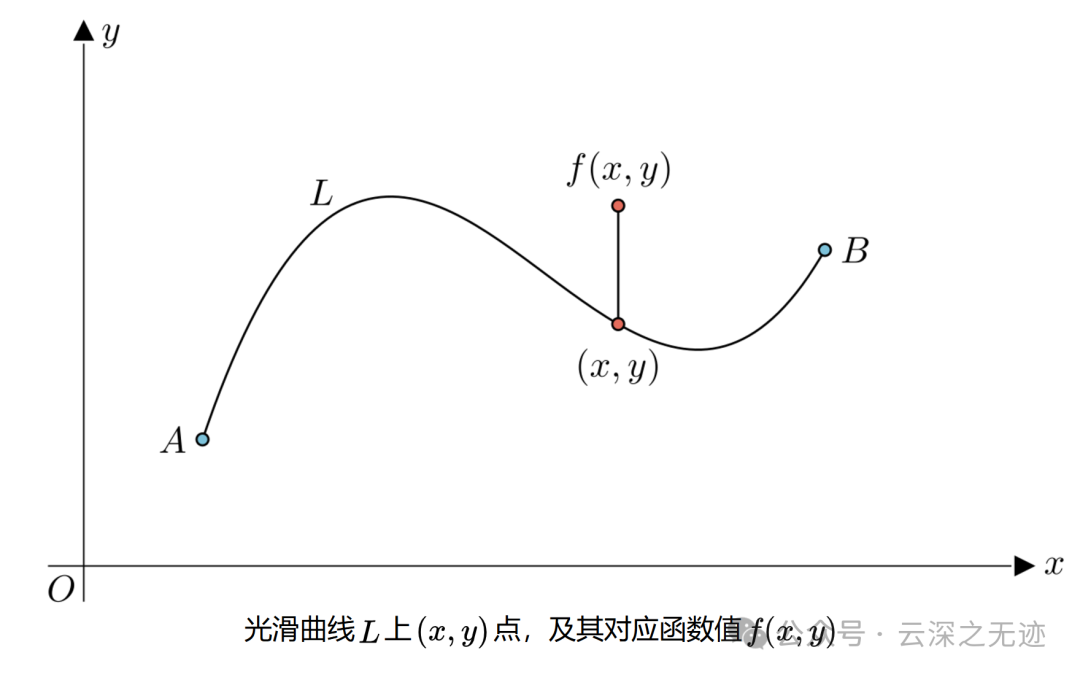
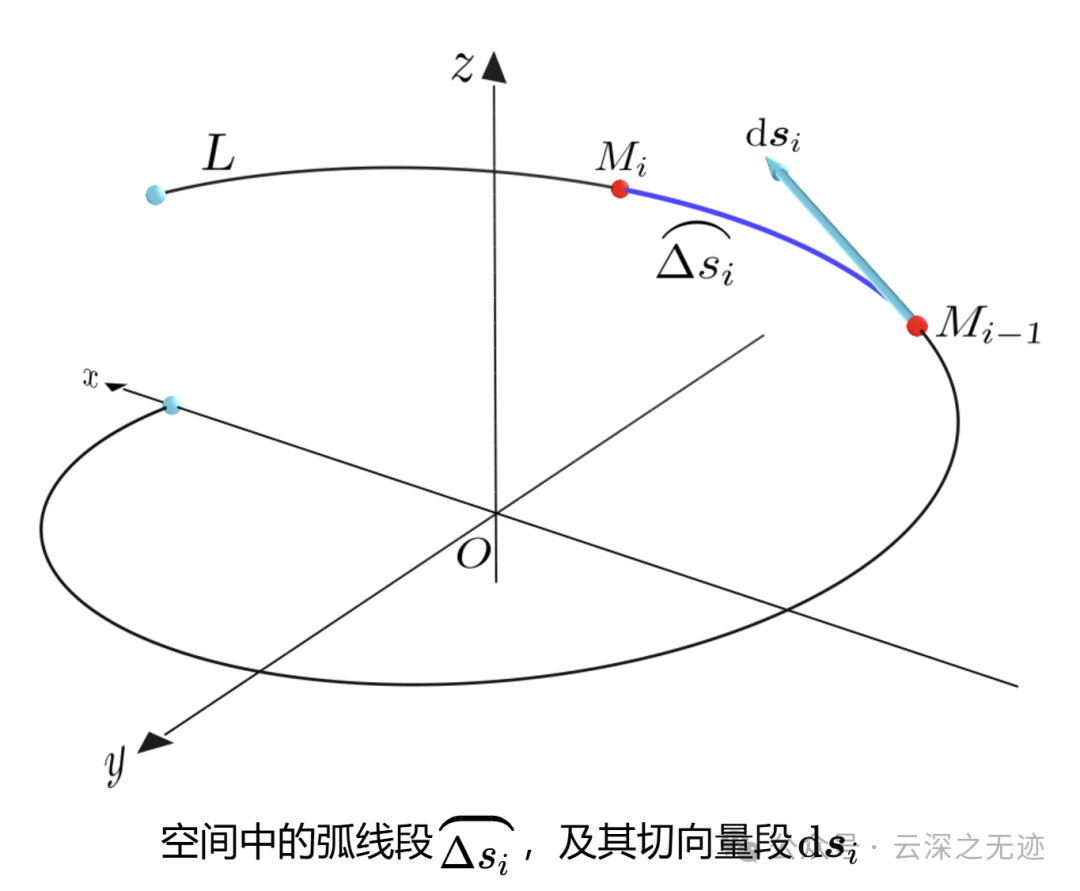
还有第二种叫第二类曲线积分，属于矢量微积分的范畴：
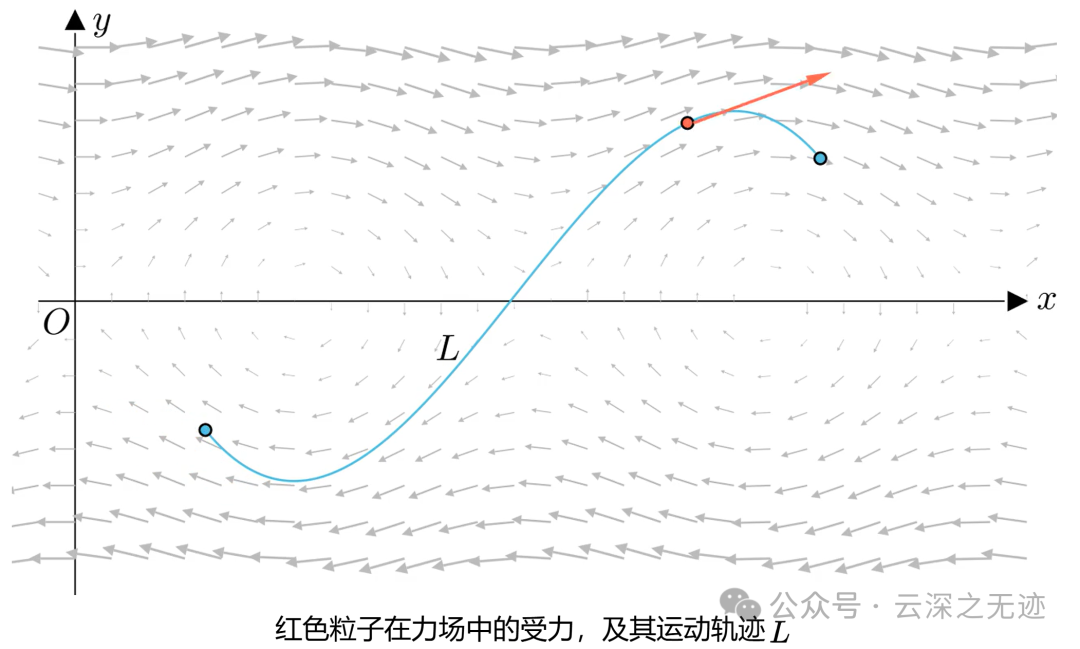
就是在一个场里面，向量函数F的有向曲线L弧上积分
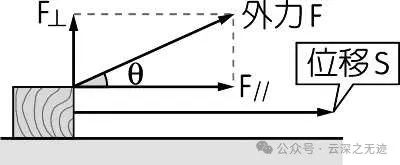
在物理里面就是求功的
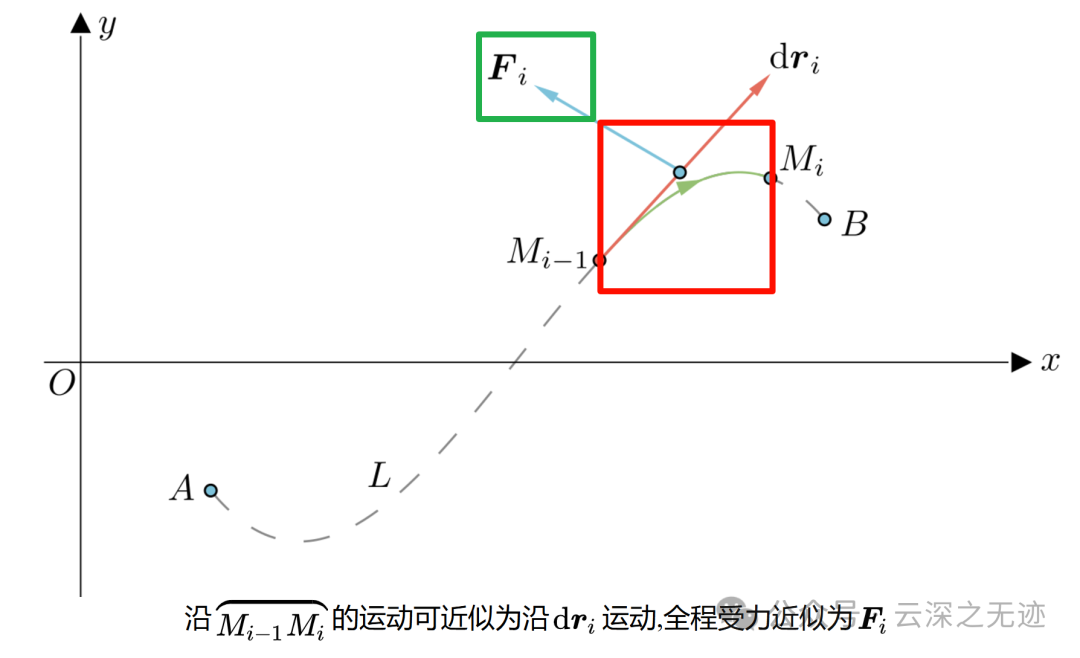
在推导的时候就是在一段弧长上面，场经过的时候做的功
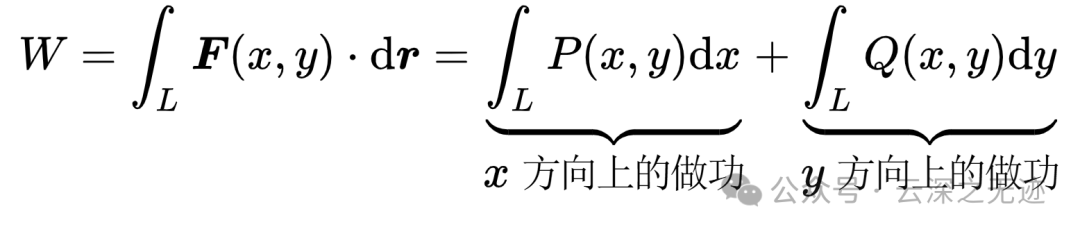
因为把好多段加起来了，所以就是这样的形式
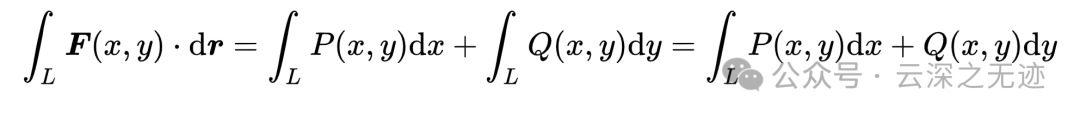
可以整体描述，也可以分成正交两部分，以及分开写
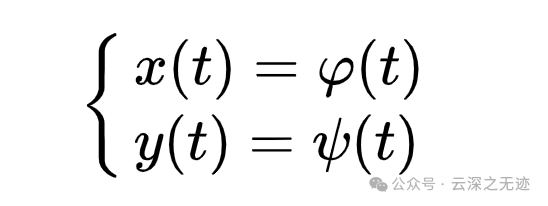
因为出现了XY子函数，不可避免的就要用参数方程的形式，这里的参数方程其实是描述的这个弧L
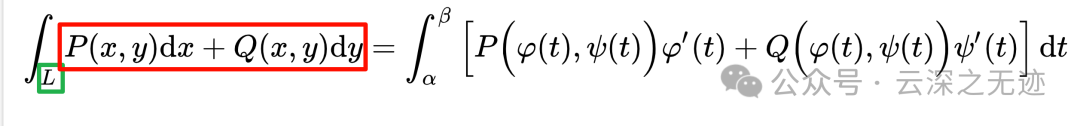
计算公式就是这样，时刻记住左下角是积分的区域，后面是积分公式，就是一个什么样的场对区域产生的累积效应。
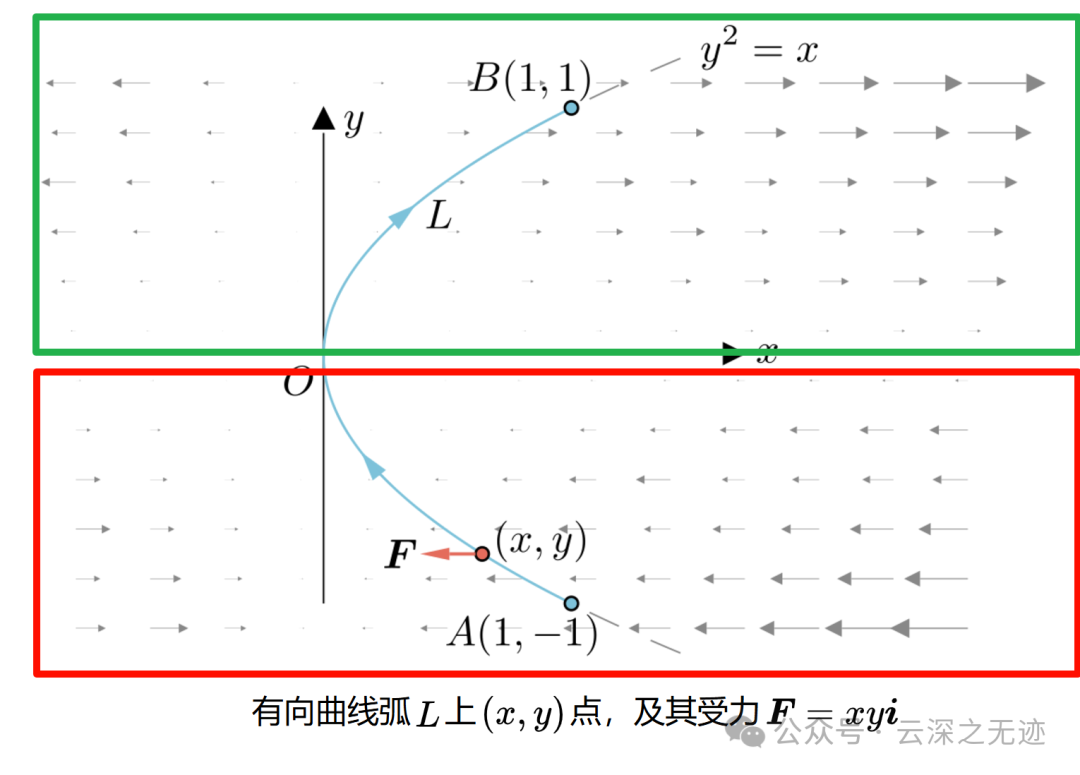
比如这个例子，就是在这个场里面，计算AB弧长上面的功。可以看到Y轴上面没有场分量的贡献。
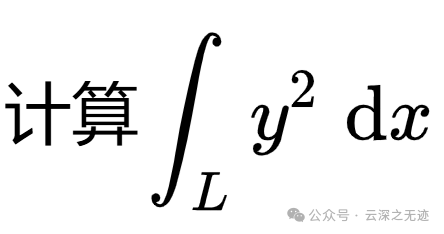
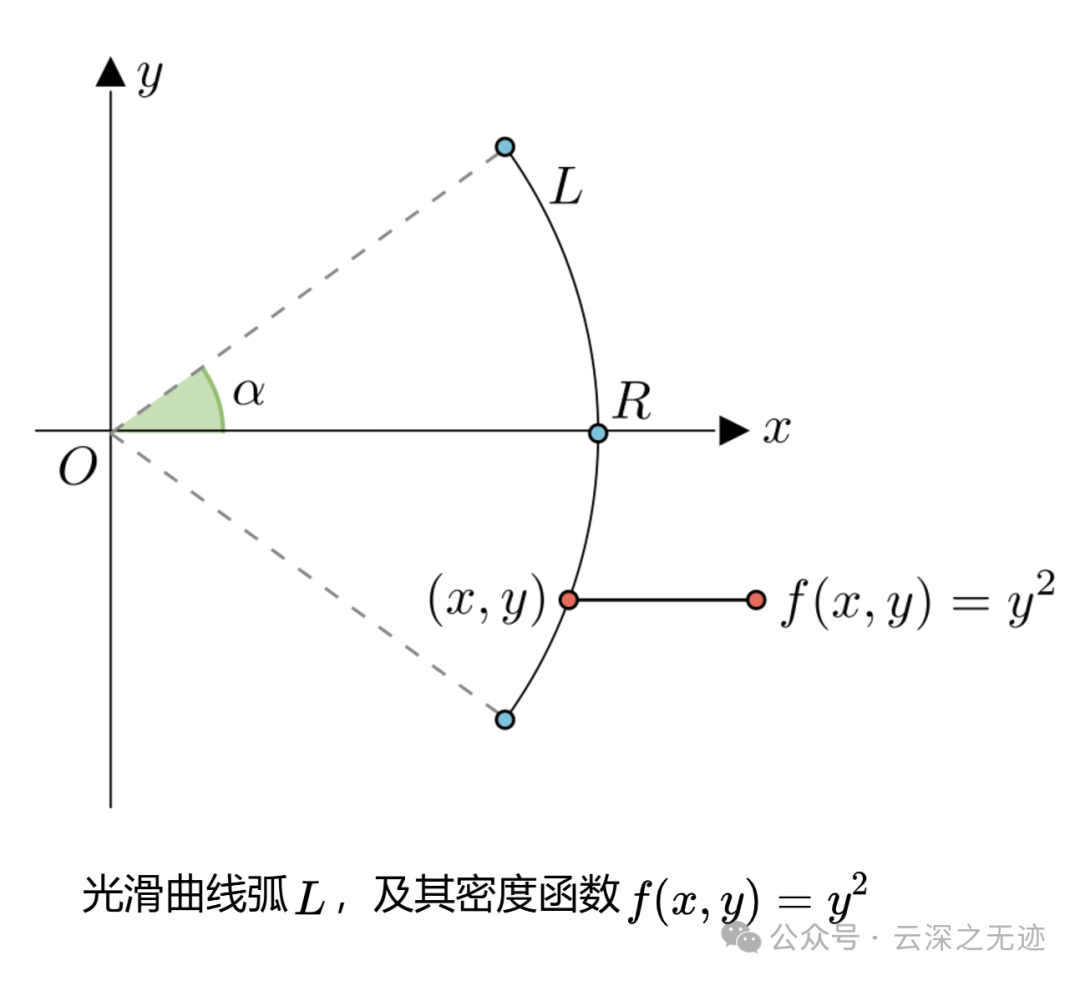
比如这个例题里面，y^2其实也是向量函数，只不过里面就有一个分量而已。
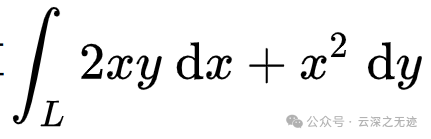
L是积分弧，后面是向量函数的两个分量，所以就可以辨认出来是曲线的第二类积分。
这样的题也是，可以从积分区域和向量场来辨认
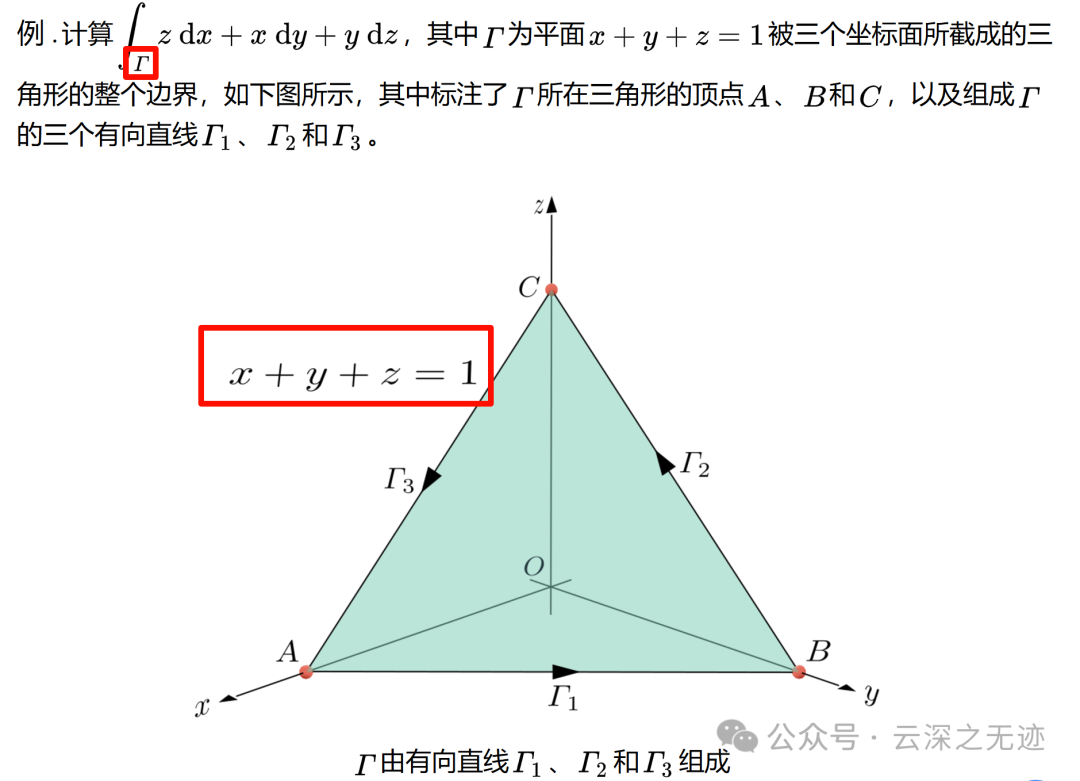
这个题应该很出名，学过高等数学的都绕不开
首先是这个平面，是一个侧着的面，墙角风。接着就是三个分向量。
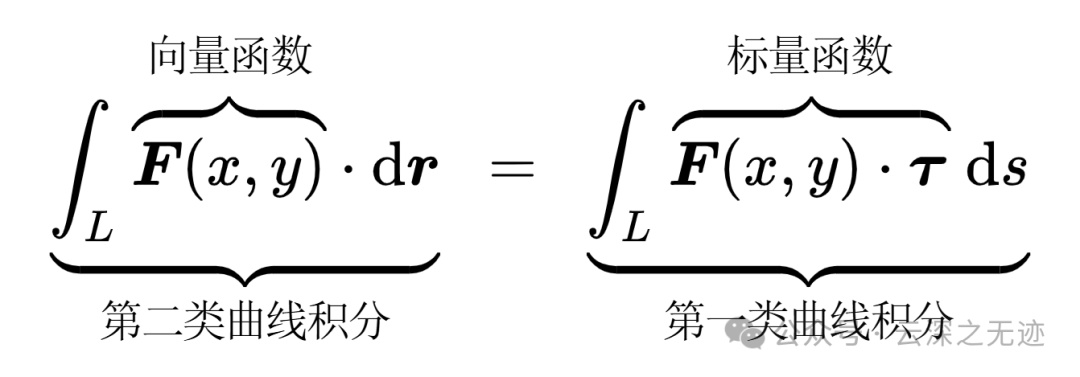
两个积分之间的关系就是标量函数的投影就是第二类的积分了，也好理解，因为就是彼此正交的场量才对积分弧有作用。
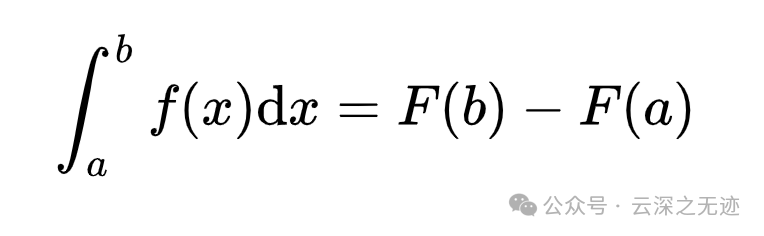
这个是微积分的第二定律，牛顿-莱布尼兹公式，简化了定积分的计算，把求积分这个事情转换成了求导数的原函数。
在这个曲线积分里面其实也有类似的定理（这里不展开讲，自己看书）
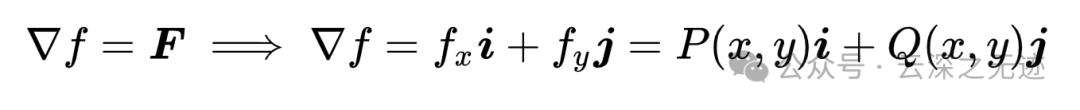
里面的符号是梯度的意思
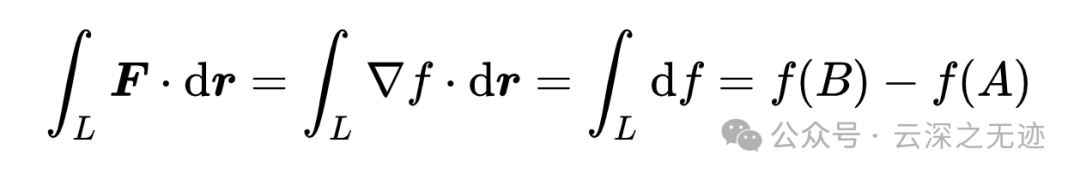
这个公式还蕴含着路径无关
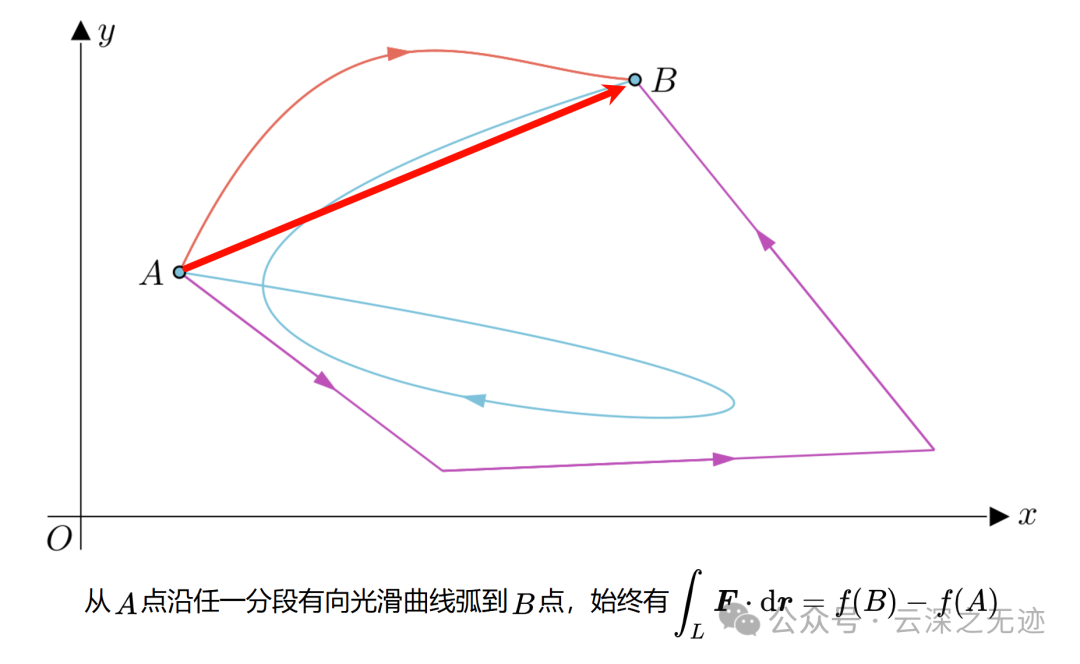
这个里面最著名的例子是克服重力做功。
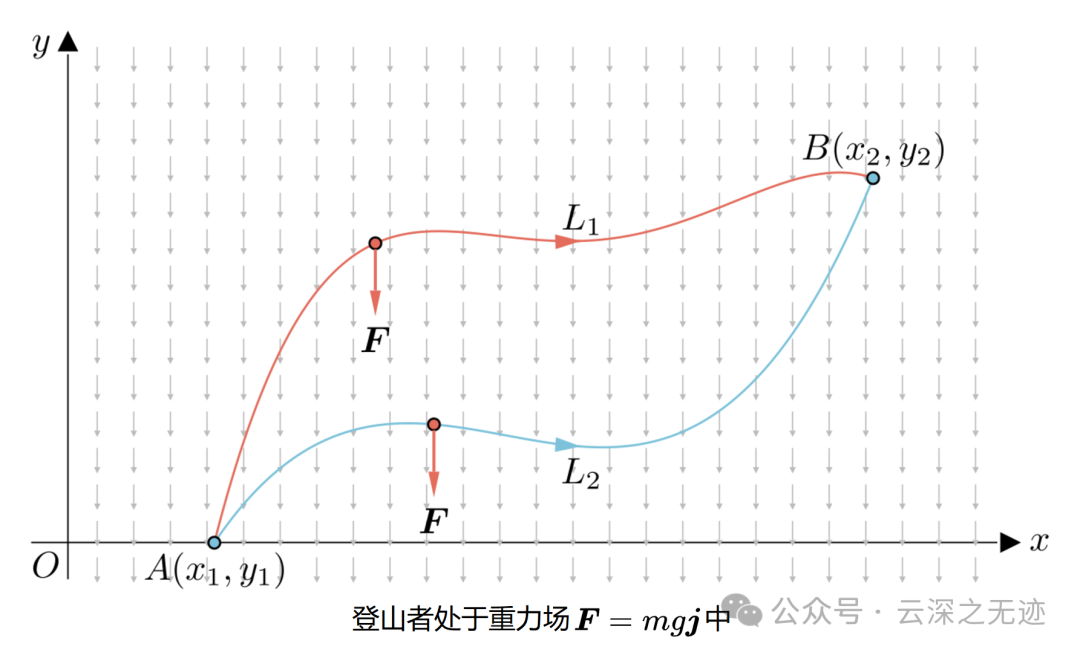
无论怎么爬大家都是一样的费力气
上面去看书，不然你可能不知道定理的使用。
存在数量函数f使得：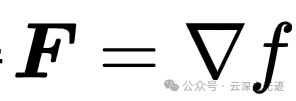
介绍一个定理，可以帮助我们判断该前提条件是否成立。
不和自己相交的曲线称为 简单曲线 （Simple curve），头尾相接的曲线称为 闭曲线 （Closed curve）。这两个概念是可以组合的：
以及有洞的复联通域
接着引入概念，有公式的成立就可以说明后面的定义
“势”指某一种特定的趋势，比如小球重力场的作用下，总有一种竖直向下运动的趋势，“势函数”反映这种趋势的大小。
这就是保守场的充要条件
路径无关的定义
闭曲线
做功与路径无关的场就是保守场，与路径相关的场就是非保守场。保守就是不变化的意思，因为从起点出发最终回到起点时能量守恒没有变化、即没增加也没减少所以称为保守场。
这里缺了保守场和路径无关的相关表述，读者自己补。
在一些条件下，路径无关和保守场是一样的
这里再对曲线积分的基本定理做一个总结。
曲线积分的基本定理，本质上是将一个沿曲线的积分转化为一个标量函数在曲线端点处的差值。
形象地说，就像我们计算从山脚爬到山顶所做的功，如果只关心起点和终点的高度差，那么无论我们选择哪条路径爬山，所做的功都是一样的。这个“功”就是曲线积分，而“高度差”就是标量函数在端点处的差值。
C 是一条光滑的有向曲线，从点A到点B。
F 是一个定义在C上的向量场，且F是某个标量函数f的梯度，即F = ∇f。
那么，曲线积分的基本定理可以表示为：
∫C F · dr = f(B) - f(A)∫C F · dr 表示向量场F沿曲线C的线积分。
f(B) 和 f(A) 分别表示标量函数f在曲线C的终点B和起点A的值。
保守向量场： 当一个向量场F是某个标量函数的梯度时，我们称F为保守向量场。
路径无关性： 曲线积分的基本定理告诉我们，对于保守向量场，其沿任意一条连接A和B的曲线的线积分的值都是相同的，即与路径无关。
计算曲线积分： 当向量场是保守场时，我们可以通过求出其对应的标量函数，然后计算端点处的函数值之差，从而快速求出曲线积分。
OK，有感觉没有？是不是类似于求原函数，代入边界求值？
是不是联系上了？
判断向量场是否保守： 如果一个向量场的旋度为零，那么它就是保守场。
曲线C必须是光滑的。向量场F必须是保守场
搞到现在都不认识保守场了，但是还是要说捏。
保守场： 如果一个向量场是某个标量势的梯度，那么它就是保守向量场。换句话说，如果存在一个标量函数φ，使得向量场F = ∇φ，则F为保守场。
在物理学中，保守场对应于保守力，如重力场、弹性力场等。保守力的做功只与物体的始末位置有关，与路径无关。
对于一个简单连通区域上的向量场F，如果其旋度为零（即∇×F = 0），那么F是保守场。旋度为零表示向量场中不存在旋涡，即场线是封闭的。
如果一个向量场F沿任意闭合曲线的线积分都为零，那么F是保守场。这意味着在保守场中，物体沿任意闭合路径运动一周，所做的总功为零。
如果能找到一个标量函数φ，使得F = ∇φ，那么F就是保守场。
假设向量场F = (y, x)，判断其是否为保守场。
计算旋度： ∇×F = (∂/∂x, ∂/∂y, ∂/∂z) × (y, x, 0) = 0。
判断区域： 整个平面是单连通的。
寻找势函数： 令φ(x, y) = xy，则∇φ = (y, x) = F。
验证： 找到的φ满足条件，因此F是保守场。
单连通区域： 在非单连通区域，旋度为零的条件不一定能保证向量场是保守场。
终于告一段落了，开始写平面积分。
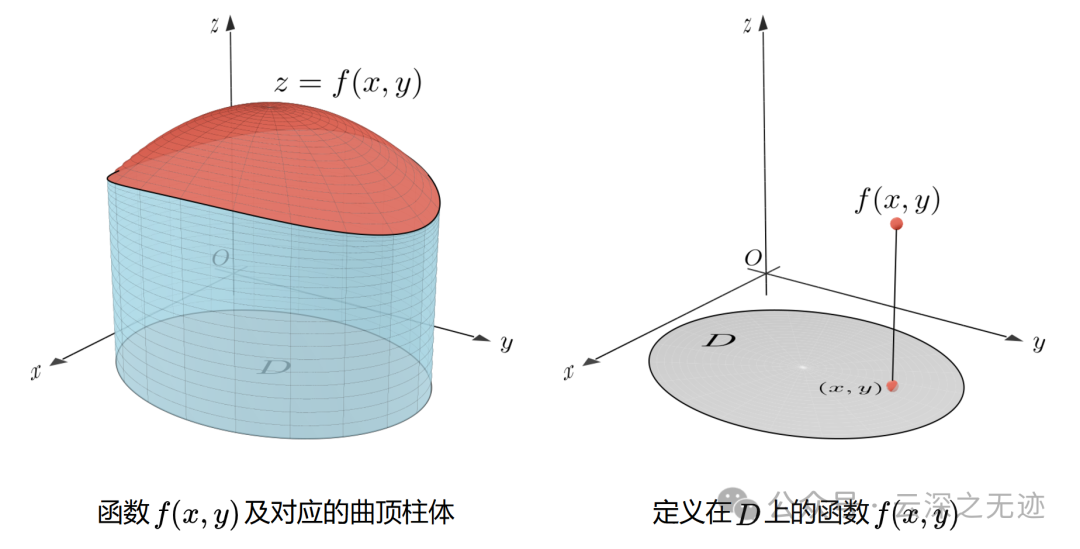
前者是二重积分，函数是曲顶柱体的体积，后面是平面区域D上的一个投影
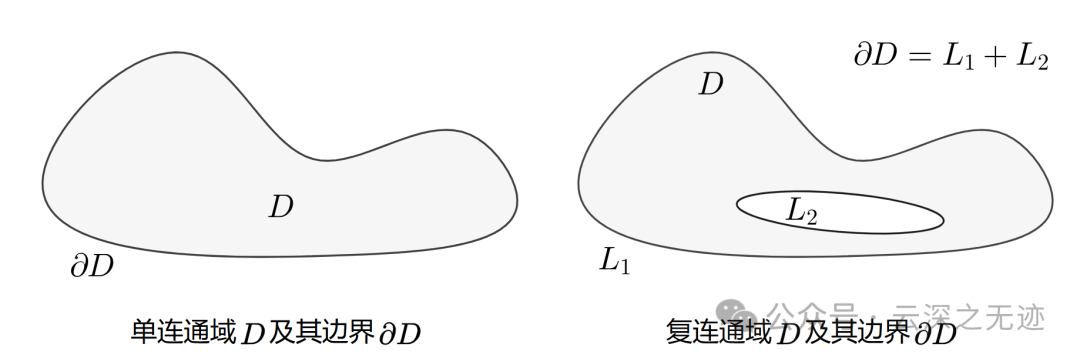
在对待曲面积分的时候，边界是一个重要的话题
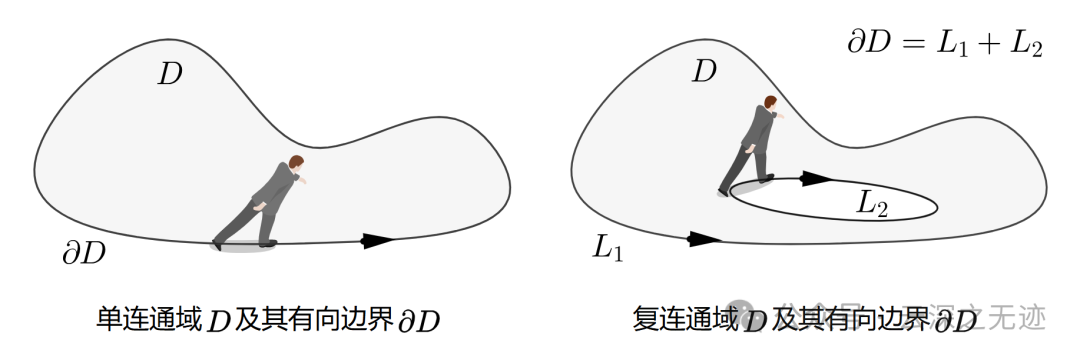
定义很简单，就是沿着线走，左手边，也就是里面的，你看第二图是不是有问题？感觉剪头不对？其实不对，我们要的边界其实是D，所以里面的边界是指向外面的。
没想到吧？上来就是格林公式！这里面的闭合区和边界是书里面一开始的内容，这里就不补了。
没有找到更好看的图，还是使用了马同学的，据说现在还是窗户上
事实上，曲线积分可能曲面积分是八杆子都打不到一起的，因为一个是弧，一个是完整平面，而格林公式把它们联系在了一起。
微积分第二基本定理和曲线积分的基本定理，两者的计算都只和端点有关。
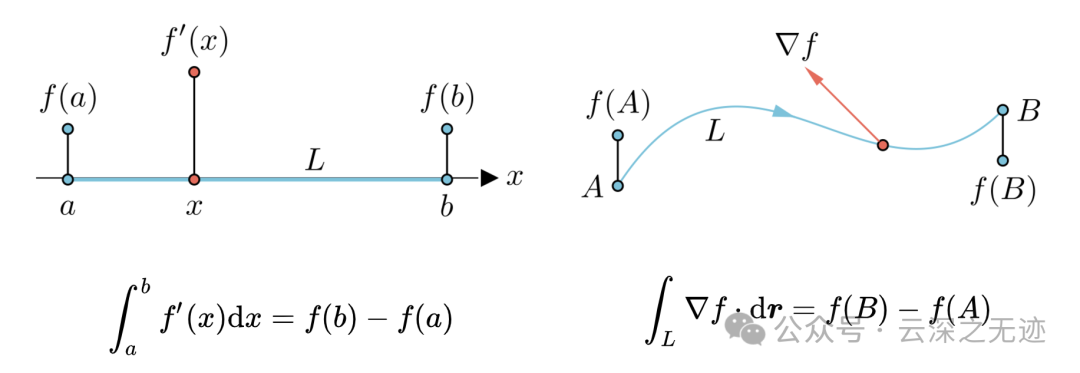
端点其实就是直线、曲线的边界，所以换句话说，两者的计算都只和边界有关。
而格林公式说的就是平面积分可通过其边界的积分来计算。
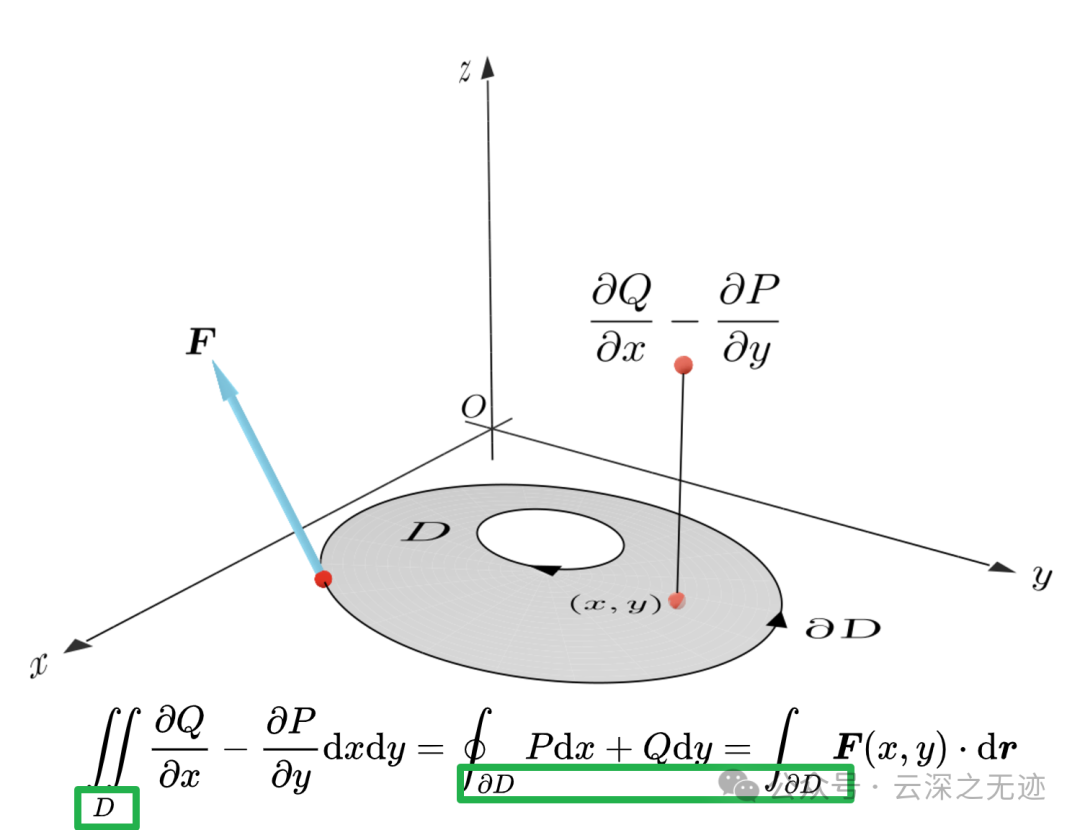
左面是闭合的区域D，右面是构成这个区域D的两个闭合线
是平面区域上的斯托克斯定理的特例。格林公式可以用来计算平面区域上的二重积分，也可以用来计算闭合曲线上的曲线积分。
更详细的推导，我就不写了，因为书上面有，放在这里还是会推到公式的本身，文章侧重于向量微积分的完整复习。
设D为平面上的一个简单闭区域，C是D的正向边界曲线，P(x, y)和Q(x, y)是定义在D上的连续可微函数，则有：
∮C Pdx + Qdy = ∬D (∂Q/∂x - ∂P/∂y)dxdy∮C 表示沿闭曲线C的曲线积分。
∬D 表示在区域D上的二重积分。
∂Q/∂x 和 ∂P/∂y 分别表示函数Q和P对变量x和y的偏导数。
格林公式可以用来计算平面区域的面积。
旋度： ∬D (∂Q/∂x - ∂P/∂y)dxdy 可以看作是向量场F = (P, Q)在区域D上的旋度的通量。
计算曲线积分： 当计算闭合曲线上的曲线积分时，如果能够找到一个向量场F，使得其旋度等于被积函数，那么就可以利用格林公式将曲线积分转化为二重积分。
高斯定理： 格林公式是高斯定理在二维空间的特例。高斯定理建立了三重积分与曲面积分之间的关系。
斯托克斯定理： 格林公式是斯托克斯定理在二维空间的特例。斯托克斯定理建立了曲面积分与曲线积分之间的关系。
例题就不放了，自己算。
我最喜欢的一个物理解释是格林公式和旋转的关系
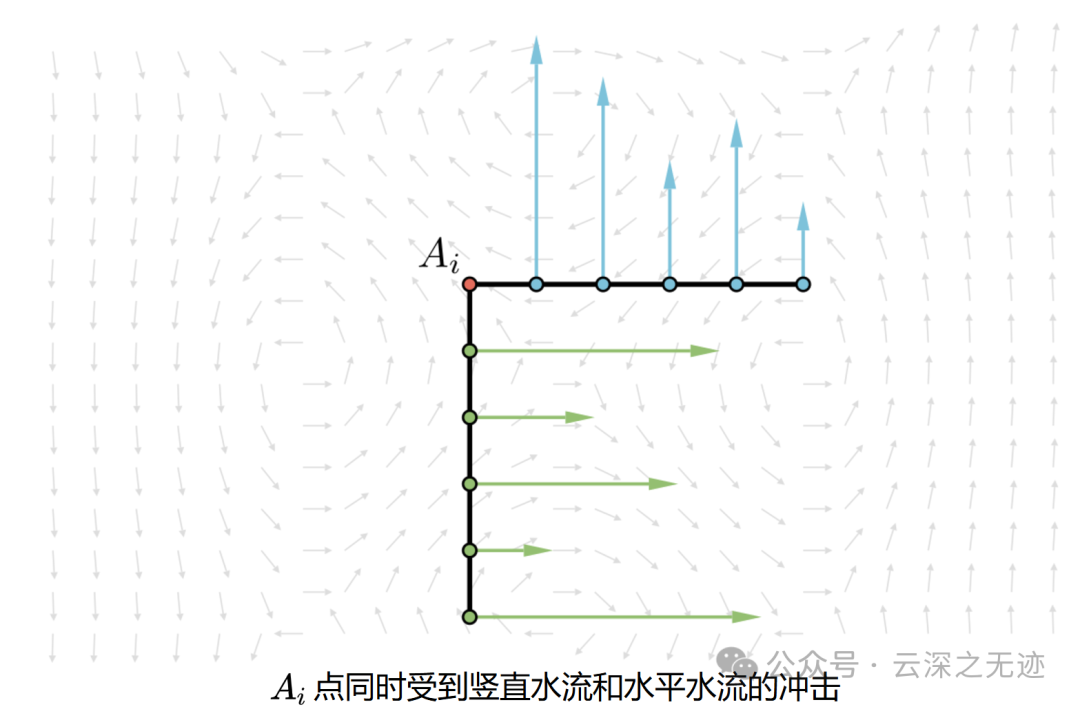
在A点处，比如有一个刚性杆子，被水冲
就出现了格林公式
将冰圈上各个点的旋转倾向累加起来就可得到冰圈的旋转。具体来说，就是设冰圈对应闭区域D，则冰圈的旋转可以计算如下，再结合上格林公式可进一步推出：
前面D是完整的一个大冰面，右边是冰面的外环
本质上是在描述一个矢量场，而格林公式正好可以用来描述平面区域内矢量场的旋转性质。
冰圈上的每个点： 可以看作是一个二维平面上的向量，表示该点的水流速度和方向。
旋转倾向： 可以理解为该向量场的旋度，即向量场在该点处的“旋转程度”。
冰圈所对应的平面区域为D。冰圈边界曲线为C。
描述冰圈上水流速度的向量场为F(x, y) = P(x, y)i + Q(x, y)j。
根据格林公式，有：
∮C Pdx + Qdy = ∬D (∂Q/∂x - ∂P/∂y)dxdy左侧的曲线积分： 表示沿着冰圈边界C的环流，也就是冰圈的总旋转量。右侧的二重积分： 表示区域D内旋度的积分，也就是冰圈上所有点的旋转倾向的累加。
因此，格林公式告诉我们： 冰圈的总旋转量等于冰圈内部所有点旋转倾向的累加。
推荐这个书
参考
旋度： 旋度是一个向量，表示向量场在某一点的旋转趋势。在二维平面中，旋度是一个标量，表示向量场在该点的逆时针旋转程度。
环流： 环流是沿着闭合曲线积分得到的线积分，表示向量场沿着闭合曲线的“环绕”程度。
电磁学里有一个环路定理，静电场的电场强度沿着任意闭合环路积分为0（电环量为0），因此静电场是无旋场。
还有一个安培环路定理，磁场强度沿着任意闭合环路积分，结果不为0，等于闭合路径所包围的各个电流的代数和乘以磁导率，因此磁场是有旋场。
一个向量场如果能够表示为某个标量函数的梯度，那么这个向量场就是保守场。首先保守场必须是一个向量场。
为什么保守场一定是无旋的？
假设向量场F是保守场，则存在一个标量函数φ，使得F = ∇φ。
根据旋度的定义，我们可以得到：∇ × F = ∇ × (∇φ) = 0 即，保守场的旋度恒等于零。
保守力做功与路径无关： 对于保守力场，物体从A点移动到B点所做的功只与A、B两点的位置有关，与所走的路径无关。这表明保守力场中不存在“漩涡”，即没有旋转。势能： 保守力场对应着一种势能，势能的梯度就是力。而旋度为零，意味着势能场是一个“平滑”的场，没有“突变”或“漩涡”。
OK，这是一个分界线。~~~~~~~~~~~~~~~~~~~~~
二重积分也称为平面积分，那么自然有曲面积分。并且和曲线积分类似，曲面积分也分为两类，标量的和向量的。
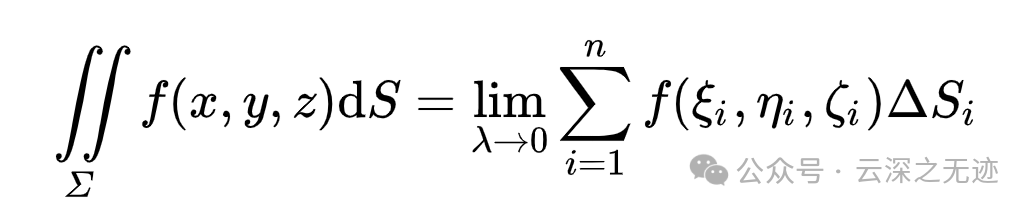
定义在此，前面就是要积分的区域，是一个区域
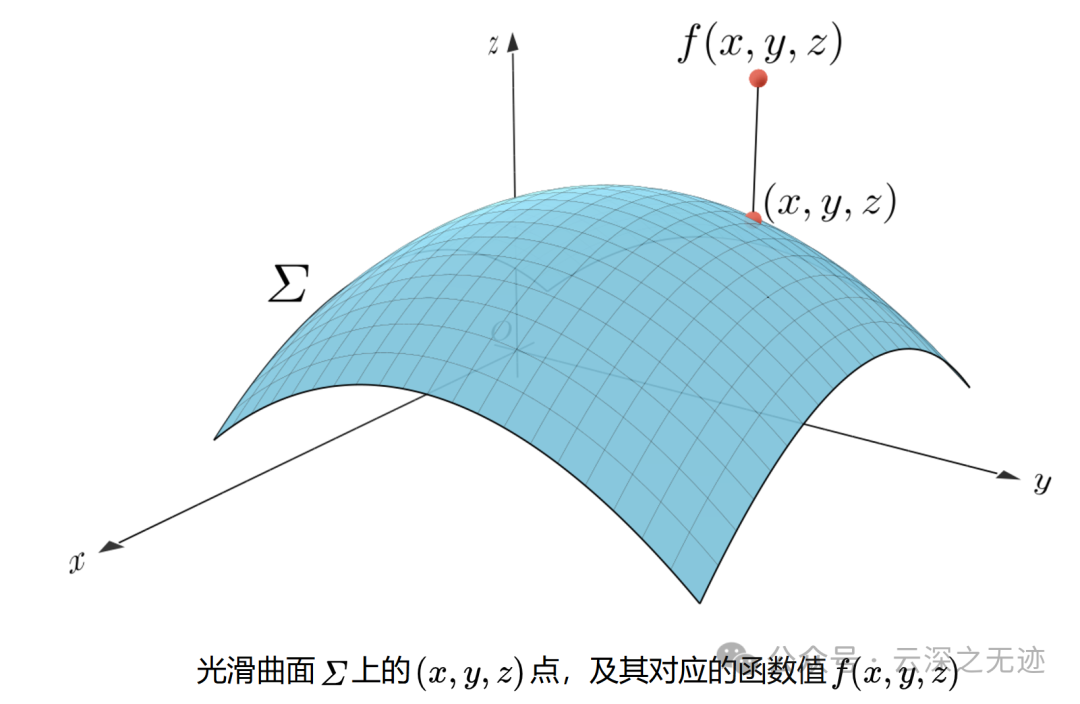
可以看到这样的
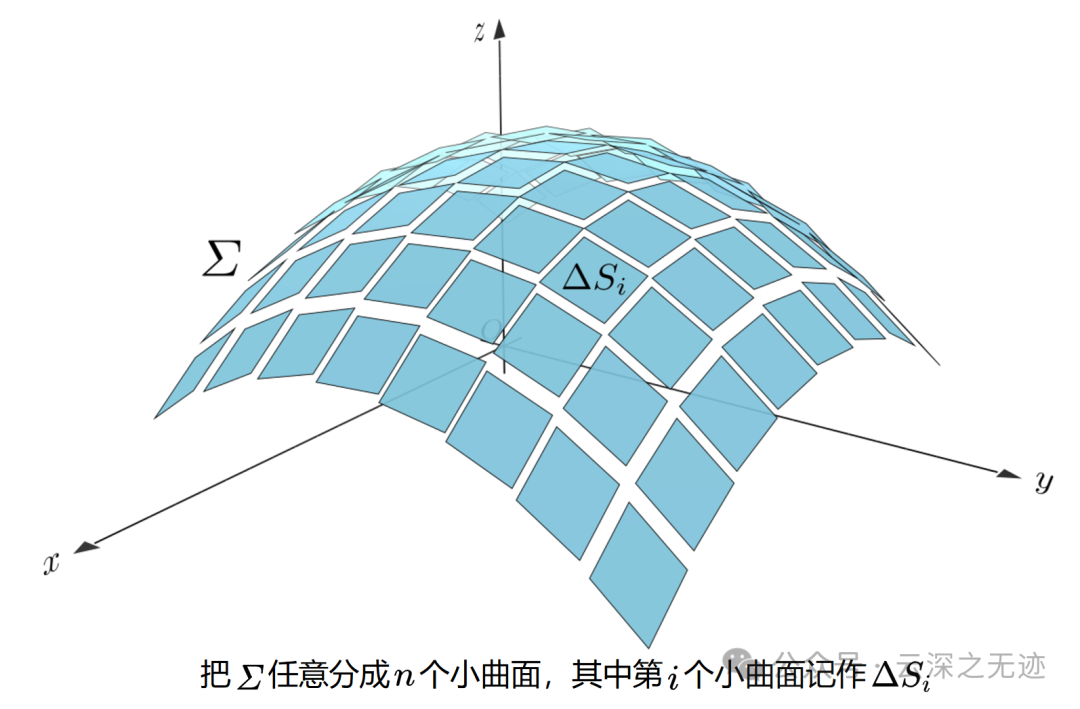
公式的右边其实就是做了分割
当然了显然的也可以对曲面做分割
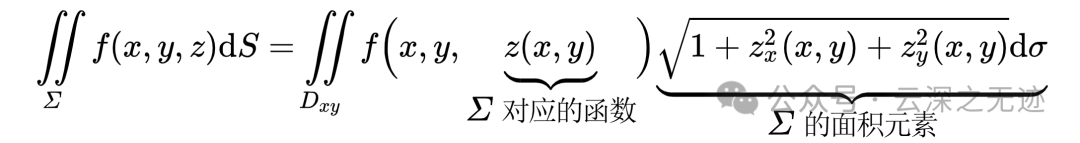
不做推导的给出计算公式，在于辨析几类积分的形式
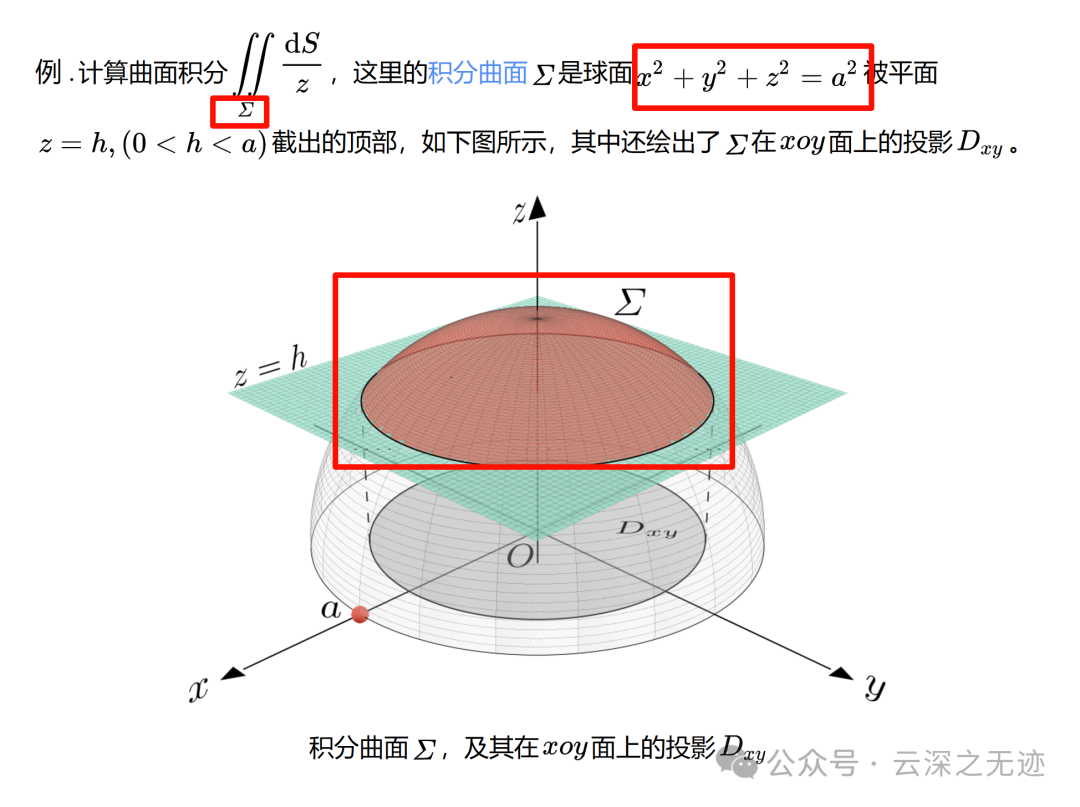
比如这个题中，关心的积分区域就是被切割的一个半球
曲面是怎么样的？
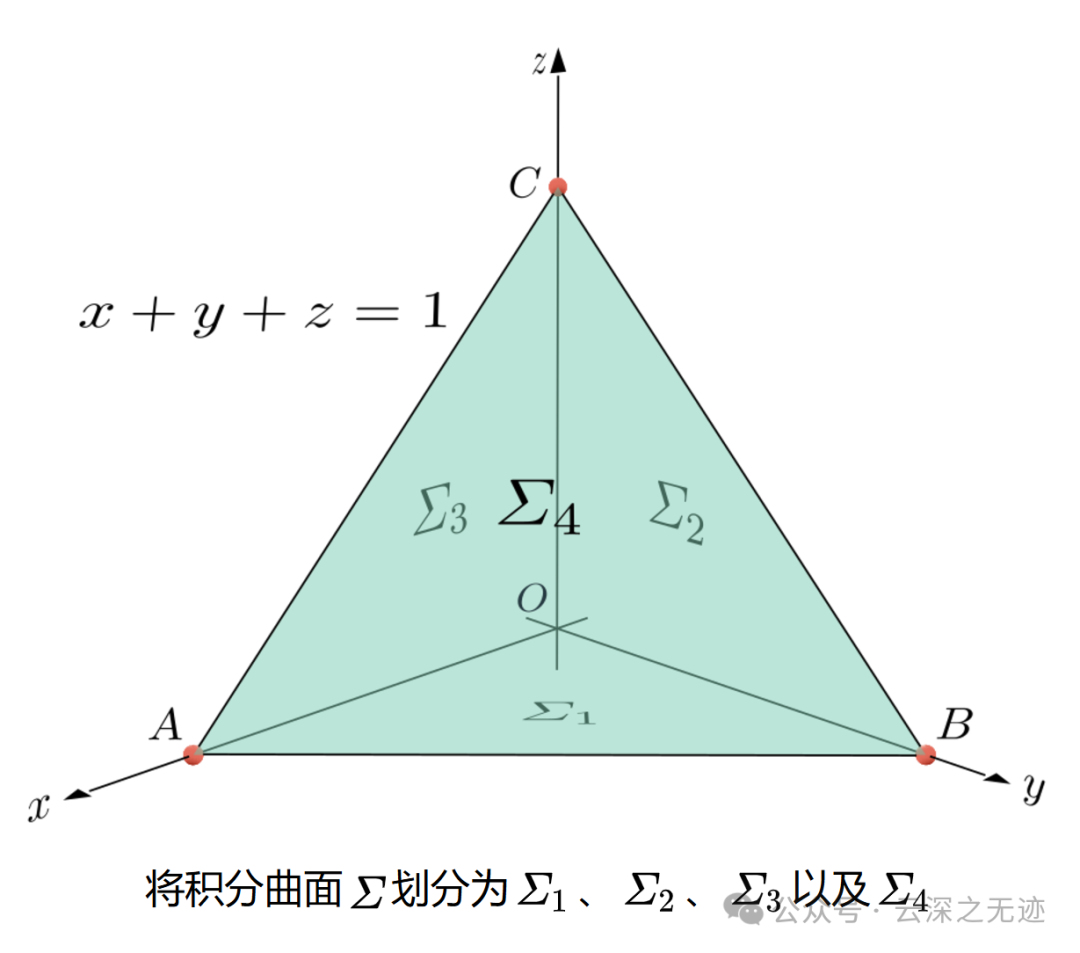
没想到吧？就是这样的一个曲面
上面是标量的积分，就是不关注方向，如果是下面这样的就需要考虑方向了。
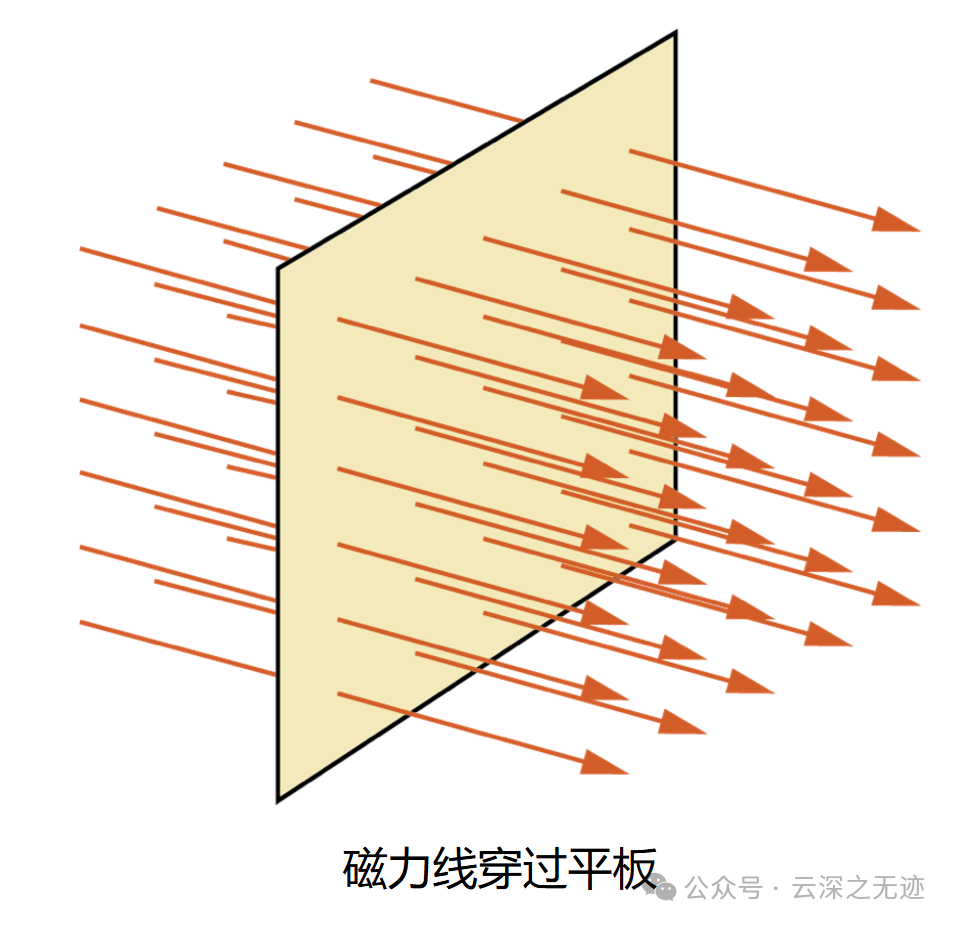
第一个问题就是定向，只有明确的方向才能说明这个小坐标系里面所有量的情况。
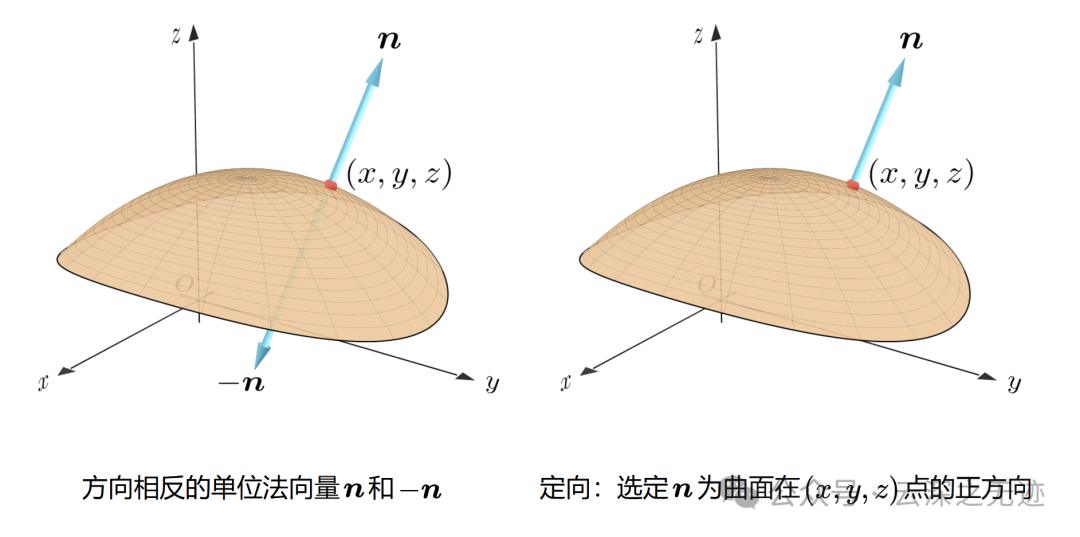
给定一个平面。上面取一点，做一个切平面，以这个点为中心，做一个⊥于切片面的线，也就是法线，我们称这个东西为一个方向向量，那么反方向顺延，也会有了负号。
空间曲面如果从数学上讲是没有厚度的，所以曲面从数学上讲没有内侧和外侧之分，只有正向和反向之分，即曲面的正向和曲面的负向。
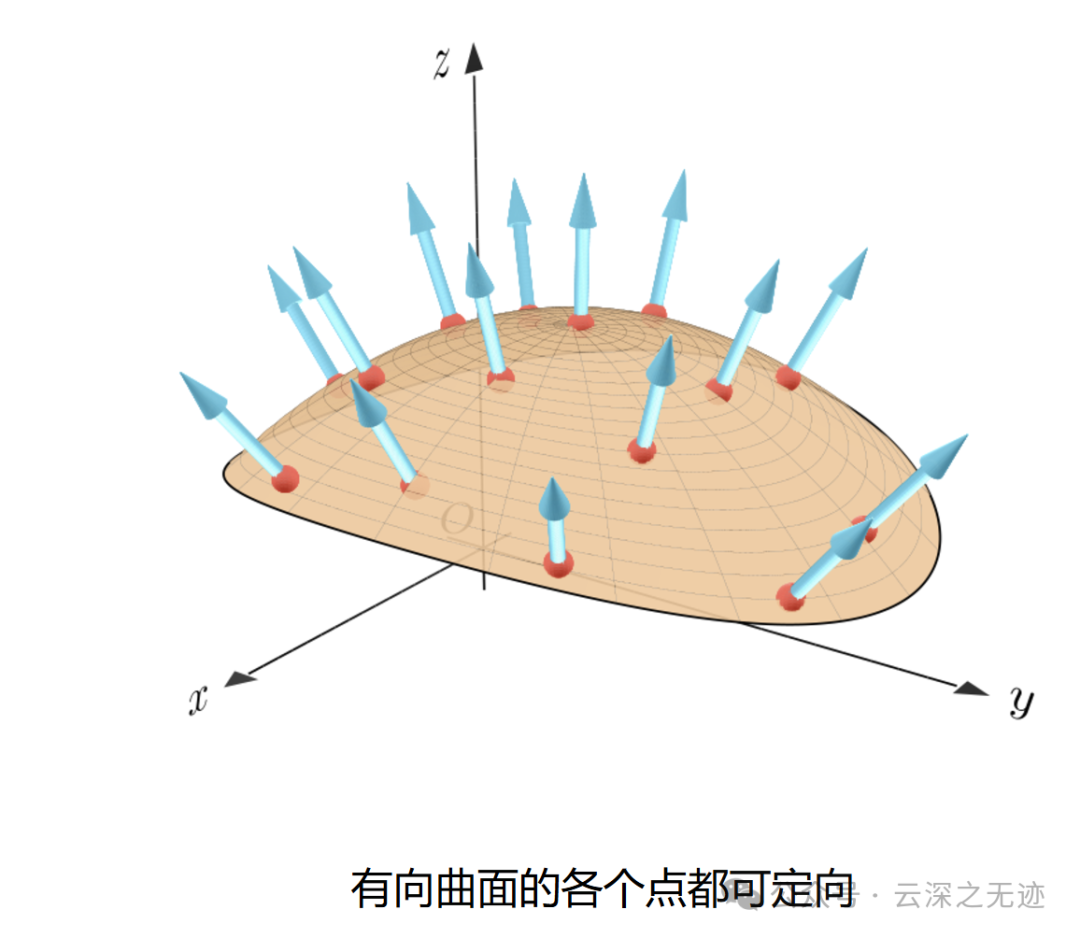
这样的叫有向曲面，都可以定向
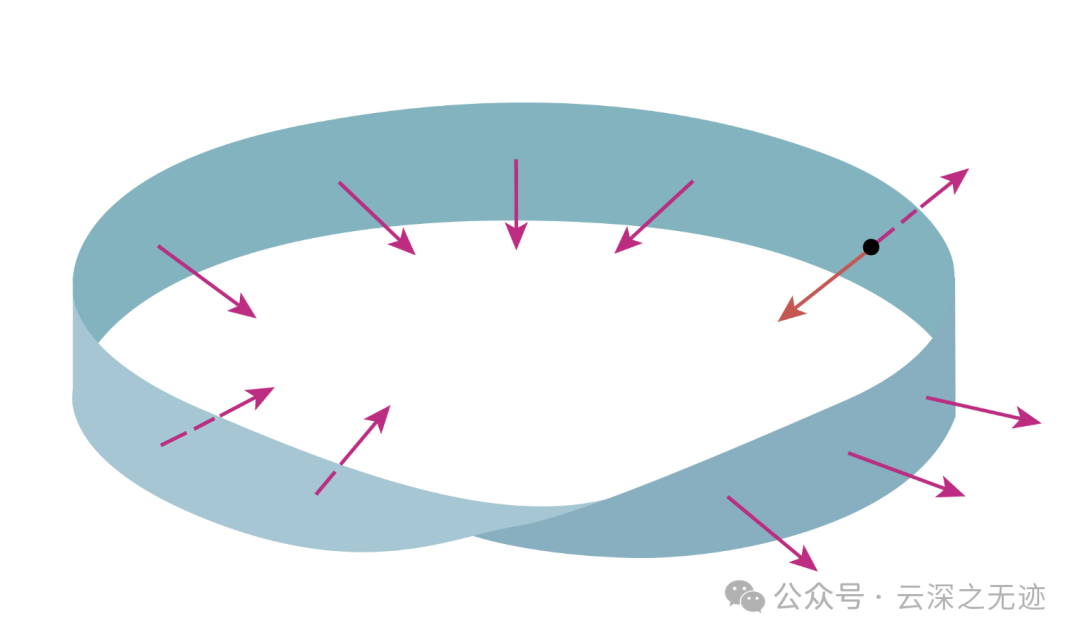
但是莫比乌斯不可以，因为转一圈方向就反了
在数学历史上流传着这样一个故事：有人曾提出，先用一张长方形的纸条，首尾相粘，做成一个纸环，然后只允许用一种颜色，在纸圈”上的一面涂抹，最后把整个纸圈全部抹成一种颜色。这个纸圈应该怎样粘？这样一个看来十分简单的问题，数百年间，曾有许多科学家进行了认真研究，结果都没有成功。后来，德国数学家莫比乌斯对此发生了浓厚兴趣。有一天，莫比乌斯到野外去散步，肥大的玉米叶子给了他灵感，他随便撕下一片，把叶子的一端扭转180度，然后对接成一个圆圈儿，他惊喜地发现，这“绿色的圆圈儿”就是他梦寐以求的那种圈圈。回到办公室，他用纸条制作了一个那样的纸环，并捉了一只小甲虫，放在上面让它爬。结果，小甲虫不翻越任何边界就爬遍了圆圈儿的所有部分。莫比乌斯环就这样被发现了。
在这里略过了，关于方向夹角的论述：
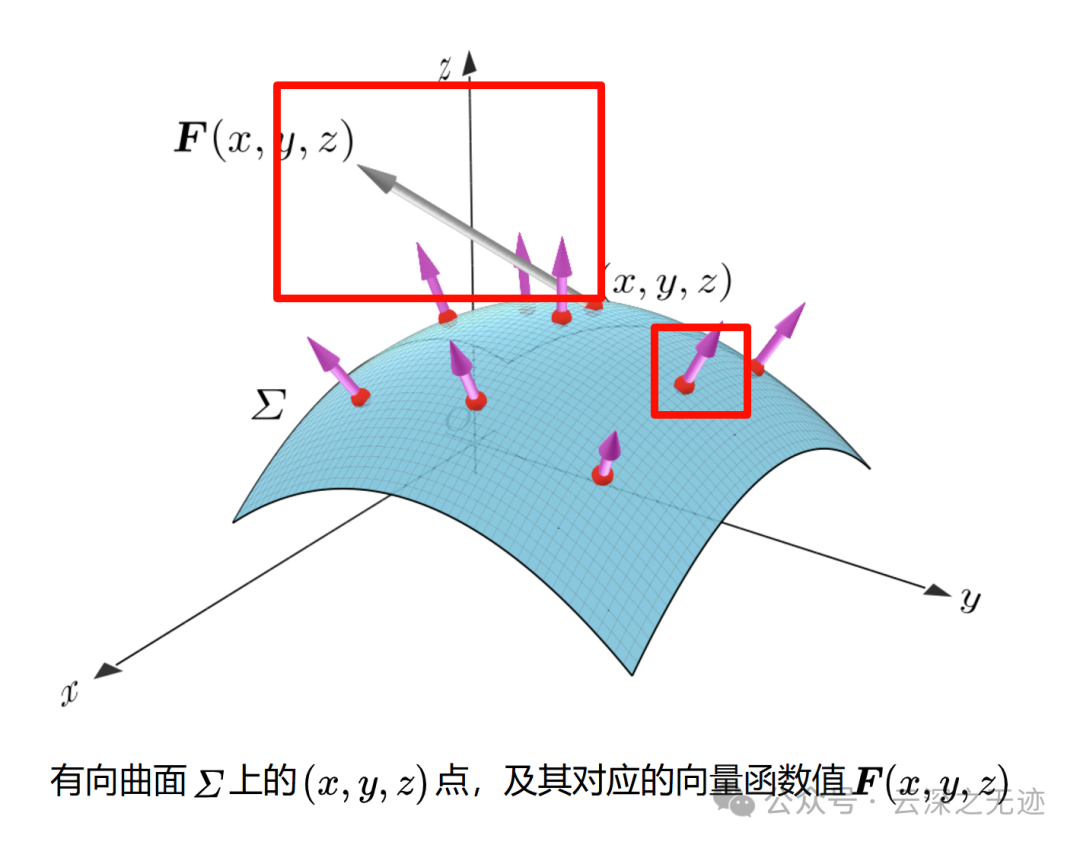
对曲面的有向积分来说，F场和每一个曲面上面可以定向的方向向量之间都有关系。
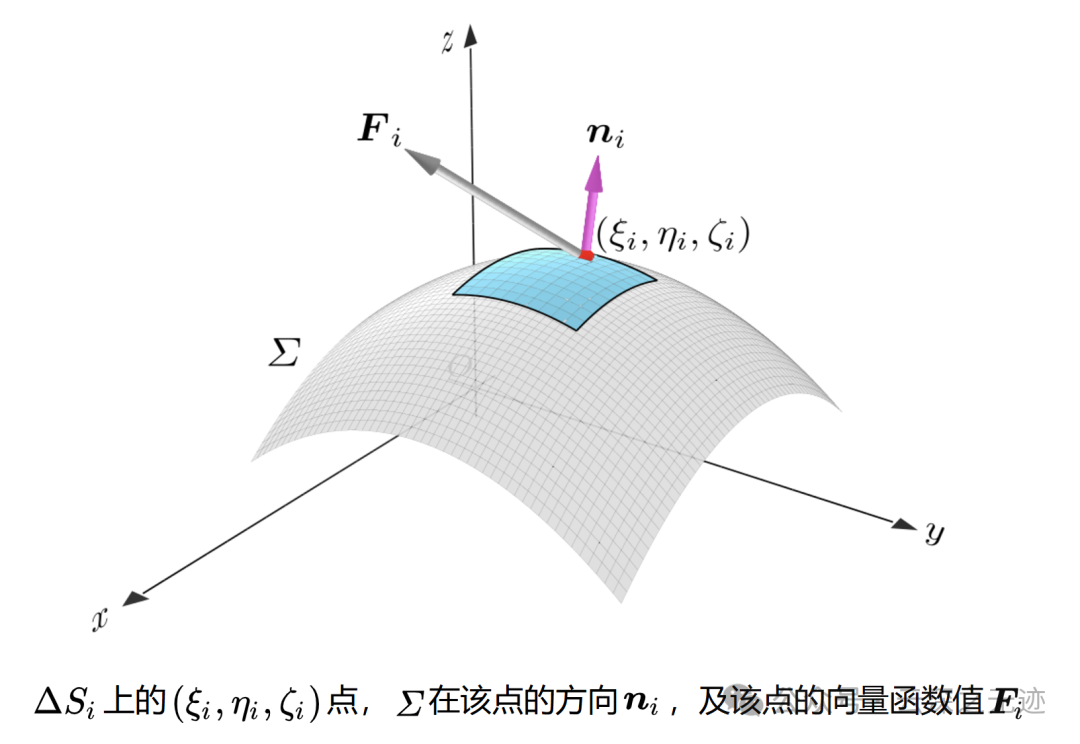
推导的时候也一样，就是取一个小面
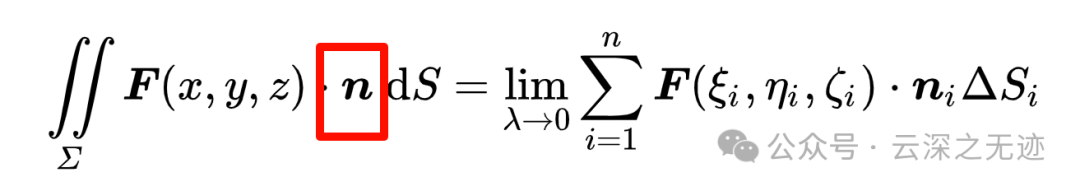
n是分隔多少块的小格子，右面是黎曼和，只有无限的时候才是和原函数相等。
计算的时候，二类是转换到一类的
不过是在前面的积分过程中蕴含了符号
通俗点说吧：
对坐标的曲面积分，是一种在三维空间中对曲面进行积分的运算。它可以用来计算曲面上的质量、电荷、通量等物理量。
就是把一个曲面分成无数个小块，每个小块上有一个函数值（比如密度、电场强度），将这些函数值乘以小块的面积，然后求和，当小块无限小时，这个和就趋近于曲面积分。
第一类曲面积分：
其中，f(x, y, z)是定义在曲面S上的标量函数，dS是曲面S上的面积元素。对标量场的曲面积分。比如计算曲面上的质量分布。
∬_S f(x, y, z) dS第二类曲面积分：
其中，F(x, y, z)是定义在曲面S上的向量场，dS是曲面S上的面积元素，且方向为曲面外法向量。
对向量场的曲面积分。比如计算一个向量场穿过一个曲面的通量。
∬_S F·dS参数方程法： 将曲面用参数方程表示，然后将积分转化为二重积分。
投影法：将一个复杂的曲面投影到一个简单的平面区域上，从而把曲面积分转化为二重积分。
直角坐标系： 最常用的投影方式，将曲面投影到xoy, yoz或xoz平面。
极坐标系： 对于具有圆对称性的曲面。
柱坐标系： 对于柱面或圆锥面等具有轴对称性的曲面，投影到柱坐标平面可以简化计算。
球坐标系： 对于球面或球的一部分。
三重积分中换元法涉及的两个坐标系 这里面就说了几个坐标系。
上面的文章里面说了几个积分里面的积分基本定理，那曲面积分有没有？
基本定理的通用就是将关于某的微分的积分运算转换成某在低一个维度的积分运算。
就是这个
其实这里已经很抽象了，可以先轻松一下。一个物体在旋转时，它的边缘会产生运动，先记住这句话。
想象一个旋转的轮子。轮子的每个辐条都在做圆周运动，这就相当于一个小的环路。如果我们沿着轮子的边缘走一圈，就会感受到一种推动我们的力，这就是所谓的“环流”。而这个环流的大小，就和轮子旋转的速度（也就是旋度）成正比。
斯托克斯定理就是将这个直观的物理现象用数学语言描述出来。
旋度： 想象一个向量场，就像是一片流动的水。如果水在某个区域内旋转，那么这个区域就有一个旋度。旋度越大，旋转越剧烈。
环路积分： 沿着一个闭合曲线（比如轮子的边缘）积分，就是计算沿着这条曲线走一圈所做的功。 一个向量场在一条闭合曲线上的环路积分等于穿过这个闭合曲线的曲面的旋度的通量。
斯托克斯定理： 这个定理告诉我们，一个向量场在一条闭合曲线上的环路积分，等于穿过这条曲线所围成的曲面的旋度的通量。
也就是说，一个区域内的旋转程度（旋度），决定了它的边界上的环流大小。
它将一个向量场在一条闭合曲线C上的线积分与该向量场在以C为边界的任意曲面S上的旋度的曲面积分联系起来。
∮_C F · dr = ∬_S (∇ × F) · dS∮_C F · dr 表示向量场F在闭合曲线C上的线积分。
∬_S (∇ × F) · dS 表示向量场F的旋度在曲面S上的曲面积分。
∇ × F 表示向量场F的旋度。
向量场： 想象一个流体场，每个点都有一个速度向量。这个速度向量场就是一个向量场。
闭合曲线： 在这个流体场中画一个闭合曲线。
线积分： 沿着这条闭合曲线，计算速度向量对路径的积分，就得到了线积分。这个线积分代表了沿着这条曲线移动一个小物体所做的功。
旋度： 旋度描述了向量场在某一点的旋转程度。旋度越大，表示该点的旋转越剧烈。
曲面： 以闭合曲线为边界，可以构造出无数个曲面。
曲面积分： 计算旋度在这些曲面上的积分，就得到了曲面积分。
无论选择哪个曲面，只要它的边界是同一个闭合曲线，那么这个向量场在该曲面上的旋度的曲面积分都相等。这个曲面积分等于向量场在闭合曲线上的线积分。
一个旋转的轮子，轮子边缘的每个点都有一个切向速度。沿着轮子边缘走一圈，你就会感受到一个力。这个力就是线积分。轮子旋转的速度（也就是旋度）越大，你感受到的力就越大。斯托克斯定理告诉我们，无论你沿着轮子边缘的哪个路径走，只要走一圈，你感受到的总力都是一样的。
饿死了，再总结一下。
格林公式： 关注的是二维平面上的情况，将平面区域上的二重积分转化为其边界曲线上的曲线积分。可以看作是一个二维的“卷曲”现象，即平面区域内向量的“旋转”与边界上的“环流”之间的关系。
高斯定理（散度定理）： 关注的是三维空间中的情况，将三维区域内的三重积分转化为其封闭曲面上的曲面积分。可以看作是一个三维的“发散”现象，即空间区域内向量的“源”与包围它的曲面上的“通量”之间的关系。
斯托克斯定理： 关注的是任意维空间中的情况，将一个曲面上的曲面积分转化为其边界曲线的曲线积分。
格林公式是斯托克斯定理在二维平面上的特例： 当曲面退化为平面区域时，斯托克斯定理就退化为格林公式。
这里缺了高斯公式，之后再补。
总得来说，曲线和曲面的相关积分都没有离开最基本的概念，把握基本概念才是最重要的。最后，这些知识的应用性极强，在力学，电磁学里面的具体场景才可能没有那么抽象。不管怎么说，这么重要的内容放在最后学的这么仓促，这种感觉一点也不好。
感谢出版社赠书哇，没想到拿到马同学正版全套
这里也打个小广告，广大的工程师，学生，研究者都可以买一套来学习，就如马同学经常说的一句话：数学走向直观才是尽头。
文章中的大部分图片出之马同学图解数学，也可以购买相关课程观看。
https://www.matongxue.com/lessons/784/parts/2427/
