最近这个信号与系统学的也是略有小成,赶紧复习一下,以及我也挺鄙视现在的教科书,全是我不爱看的(小装一手B)。{这篇文章写了太久了,根本没有办法再拾起来把后面的补上,先发出来吧}
信号与系统-时域分析-微分方程求解.茅塞顿开版
信号与系统的书籍都一样,一开始就写关于一些系统的概念。但是最难的部分一定是微分方程求解这一部分,我之前写过一次,但是还是没有那种水到渠成的自然感觉,这次不一样了。
书里面写的不精炼,也写的不清楚。(事实上我不如教科书)
先明确一点就是,微分方程的求解是一个绕不开的坎,只能搞懂。
有俩大类,4种求解:
零输入响应: 系统在没有外部输入的情况下,仅由初始状态(如电容的初始电压、电感的初始电流等)引起的输出响应。反映了系统内部能量的衰减或振荡过程,与系统的初始状态密切相关。
零状态响应: 系统在初始状态为零的情况下,仅由外部输入引起的输出响应。反映了系统对外部输入的反应,与系统的传递函数密切相关。
完全响应: 系统的完全响应是零输入响应和零状态响应的叠加。包含了系统的所有特性。
冲激响应: 系统对单位冲激信号的响应。是系统的一个基本特性,完全表征了系统的动态特性。
阶跃响应: 系统对单位阶跃信号的响应。更直观地反映了系统的动态特性,如上升时间、峰值时间、超调量等。
一大类是求解
0输入,就是自己内在原有的。0状态指的是能量注入的时刻,所以这里的状态指系统的能量的时间。初始值通常是指系统状态变量在t=0时刻的值。
至于下面两个给系统注入不同能量的形式。
接下来继续说,因为一些系统本身就自带能量,初始状态的存在: 系统在t=0时刻可能具有非零的初始状态(如电容的初始电压、电感的初始电流),这些初始状态会引起系统的输出。
如果零输入响应随着时间趋于零,则说明系统是稳定的;否则,系统是不稳定的。也就是说能量会逐步的释放掉。
想象一个秋千。当你用力推一下秋千后松手,秋千就会荡起来。这个时候,没有外力作用在秋千上,秋千的摆动就是一种零输入响应。秋千最终会停下来,这是因为空气阻力等因素消耗了秋千的能量。
在电路中, 电容和电感就像秋千一样,它们可以存储能量。当电路中没有外加电压或电流时,这些存储的能量就会逐渐释放,导致电路产生一个衰减的响应,这就是零输入响应。
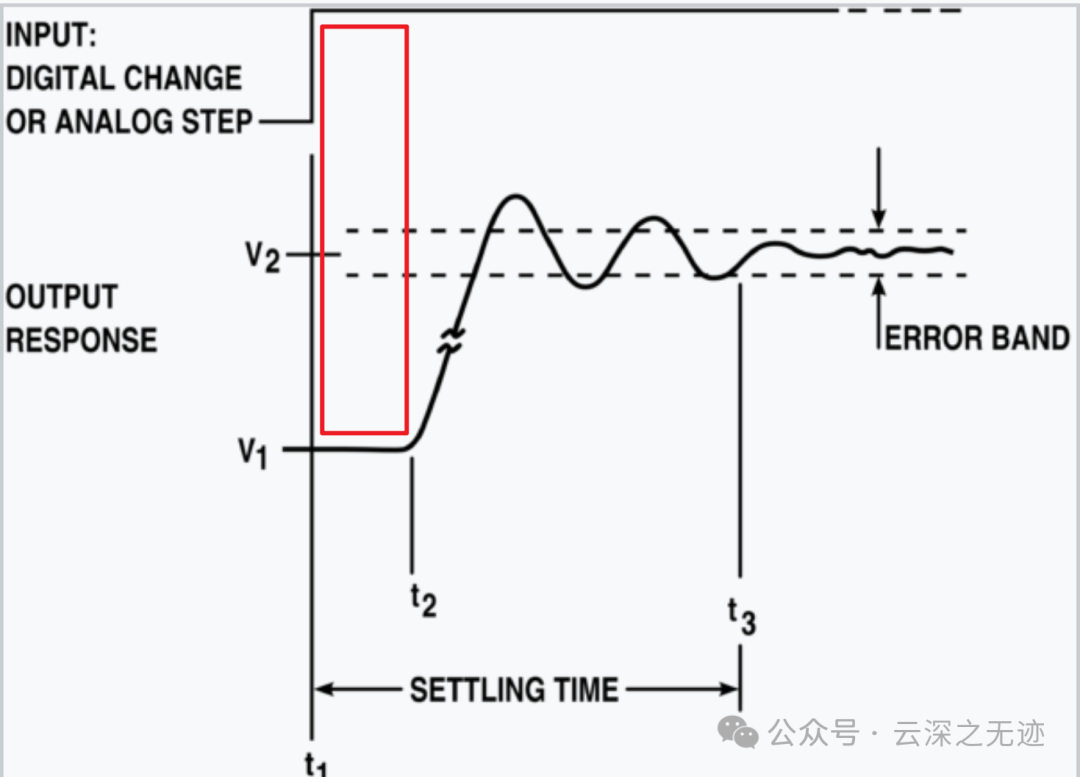
阶跃响应是一般系统在输入在极短时间内从零变为一时输出的时间行为
这里讲的是:阶跃响应指当一个线性时不变系统(LTI系统)的输入是一个单位阶跃函数时,系统的输出响应。
换句话说,就是当我们给系统一个突然的、持续的输入时,系统如何反应。
阶跃响应可以反映系统的很多特性:(我们测试运放其实就是这样干的)
上升时间: 系统输出从10%上升到90%所需的时间。
峰值时间: 系统输出达到第一个峰值的时间。
峰值超调量: 系统输出的最大值与稳态值之差,反映了系统的振荡程度。
调节时间: 系统输出进入并保持在某个误差范围内的最短时间。
阶跃响应的数学表达式通常比冲激响应简单,而且更容易测量。这样一来,我们现实的工程就好用了
想象一下,你给一个水桶注水。刚开始水位上升很快,然后逐渐变慢,最后水位稳定下来。这个过程就类似于一个系统的阶跃响应。通过观察水位的变化,我们可以了解这个水桶的特性,比如它的容积、漏水速度等。
冲激响应反映了系统对一个极短的、能量无限大的脉冲信号的反应,它包含了系统的所有动态特性。
他们俩者互相对偶:
互为变换: 冲激响应是阶跃响应的导数,而阶跃响应是冲激响应的积分。
信息含量: 冲激响应包含了更多的信息,因为冲激信号包含了所有频率成分。阶跃响应则相对来说丢失了一些高频信息。
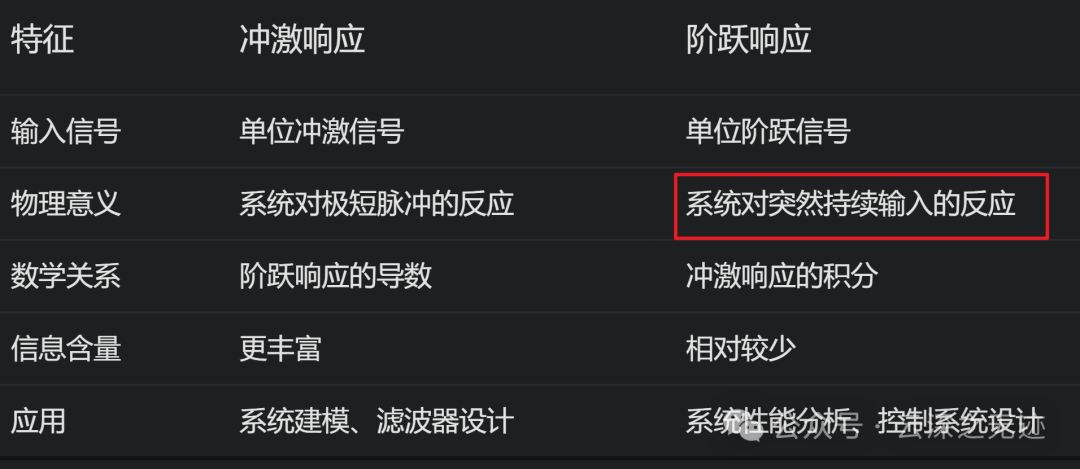
冲激响应 好比给一个静止的池塘扔一块石头,水面产生的波纹就是冲激响应。
阶跃响应 好比给一个水池不断注水,水位的变化就是阶跃响应。
上面都好说也都好理解,真正难得问题还是解方程要用哪个条件。
我们要以时间节点分,就好像求导数一样。- 0 +
-的时候有着系统内部的能量。也叫历史信息,这个时候可以认为系统已经稳定。里面有着个电容的电压和电感的电流值。这个时刻可以确定t0-的系统响应和响应的各阶导数。另外,电容是开路,电感是短路 这里还蕴含着一个所谓的换路定理。
0的时候就是外部的能量引入了。在t0+的时候,储能的连贯性,电压和电流都不会突变的。+ = -
也是就说Vc(0+)=Vc(0-),iL(0+)=iL(0-),那这个时候的系统响应就是两部分了,一开始有的能量和现在新注入的。
由于外加激励让系统改变了,系统的初始值与初始状态不一样了。那这样就只能使用初始值不能用初始状态了。就是只能使用外部激励了,内部因为这个激励已经变了,就是电压电流都变了,不确定了。
系统的初始值=0输入+0状态。(注意里面都是有各阶导数的)
在0输入的情况下,且系统的内部结构和参数不变,有全部连等的成立。
我想说的是,抓住这个量有没有变换,0输入就好像一个水杯,如果系统变换,我们就不知道杯子里面的东西有多少了,其实我们就是追求可控,只有知道具体的量才能列等式计算求解。核心思想是这样的。
所以就是看这个激励信号对初始值和初始状态的影响。
0输入响应是齐次方程的解。
0输入响应的形式与系统的结构和参数有关,而这个待定系数的大小要由系统的0+的值和相关的导数有关。
在0输入条件下,只要内部的结构和参数不变化,
0输入响应是齐次方程的解,但不是系统的齐次解。
当我们将系统的输入置为零时,所得到的输出就是零输入响应。齐次方程是指等号右侧为零的方程。将描述系统的微分方程的输入项置为零时,得到的方程就是一个齐次方程。
系统的齐次解: 系统的齐次解是指齐次方程的通解,它反映了系统本身的固有特性。因为零输入响应是在输入为零的情况下得到的,而输入为零恰好对应着齐次方程。
零输入响应不是系统的齐次解: 因为系统的齐次解是一个函数族,而零输入响应是这个函数族中满足初始条件的一个特定解。也就是说,零输入响应是齐次解的一个特例,而不是整个齐次解。

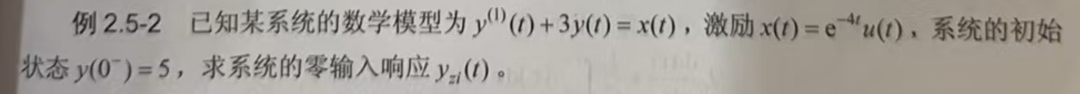
求这个,0输入响应

OK,A怎么求?
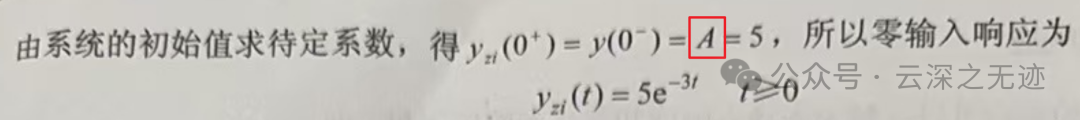
因为求的是0输入,所以就是之前的能量等于现在现在的输入,因为在0时刻没有突变。

OK

一般到二阶就够了,使用这个表就可以求解了
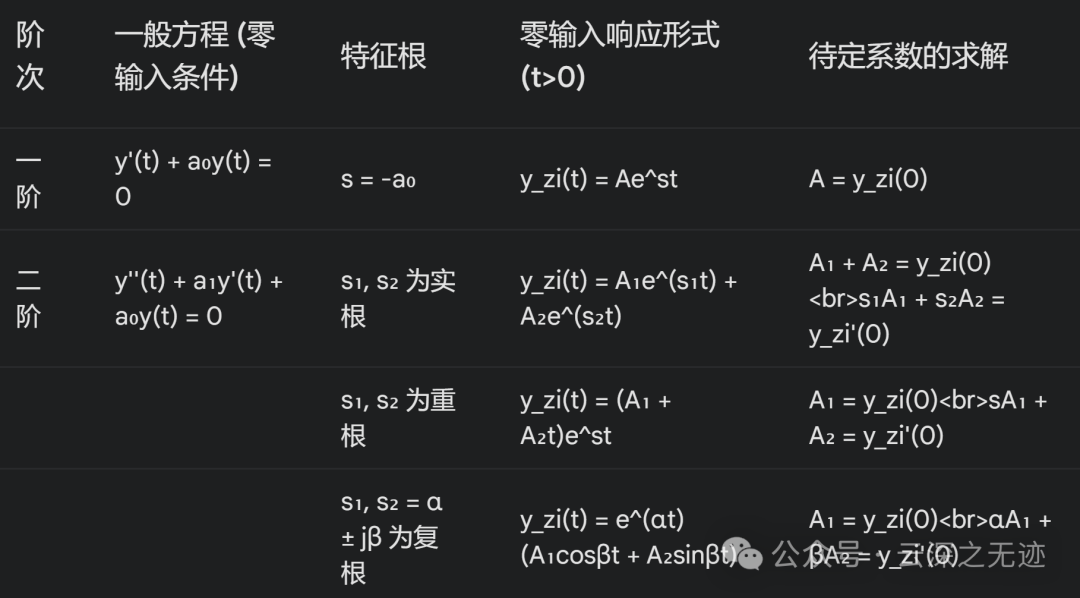
其实就是因为解方程缺东西,按照抽象的物理模型考虑外面的能量到底有没有和来以前的状态做比较。以后不说大话了,确实是不如教科书。