文章写了三个事情,球面坐标如何记忆,柱面坐标的取值特殊性,最后还补充了圆锥面的一种思考方式。 自己
在三重积分里面因为多半是一个立体的区域,还有就是这个重积分的换元法,有一种是球面坐标系,里面有几个角度,这里现在辨认一下。

好像和书上的不一样标记,我先记得是极角

因为前者是一个单独的Z轴,所以这个的范围就是0-2π,也就是180°,接着就是下面XOY,也就是我们说的方位角了,平时用的多。

先说距离 ,然后说立体的角度,接着旋转的角度确定方位

一般也不记得推导,就记得下面这个往直角坐标系下面转换的公式,最里面的是极角。先这样记,后面的:

这两个是在XOY平面上面的XY,最好记。前面的就是SIN,Z这个好想就是,COS本质上面是个投影。
后面的φ是平面的,所以范围是2π,polar是π,因为就是一个线上。
特别的还有一类是柱面:
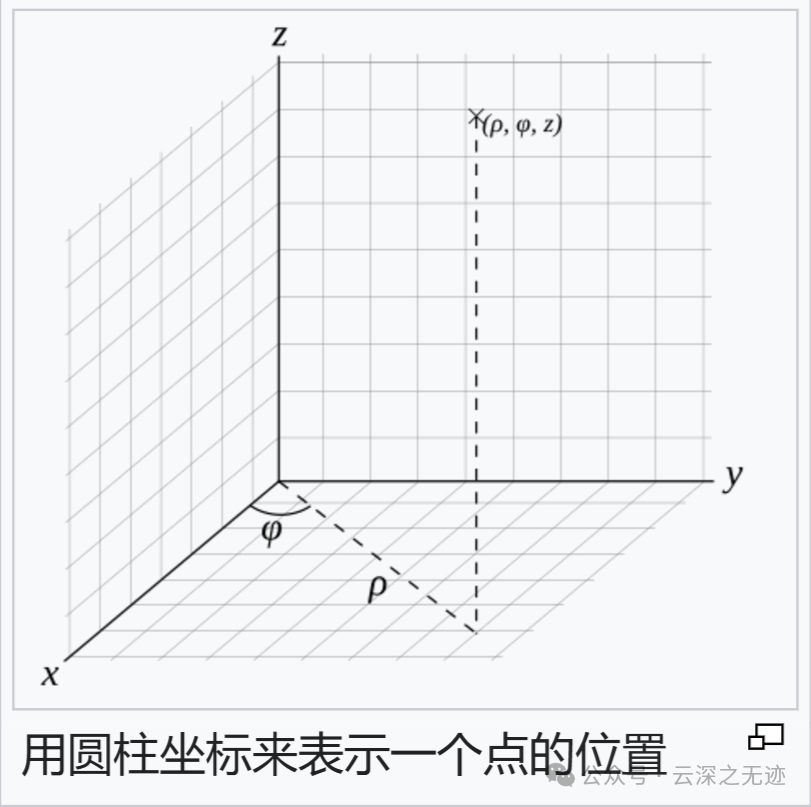
就是这样的,它的Z是不固定的

中间的参数是没有限制的,因为上下通透。角度是0~2π的,因为旋转一周。但是这个rou(这打字法,服了),是从0到♾️,因为可以无限的延长。
本来就结束了,但是还缺一个锥面,补一下:
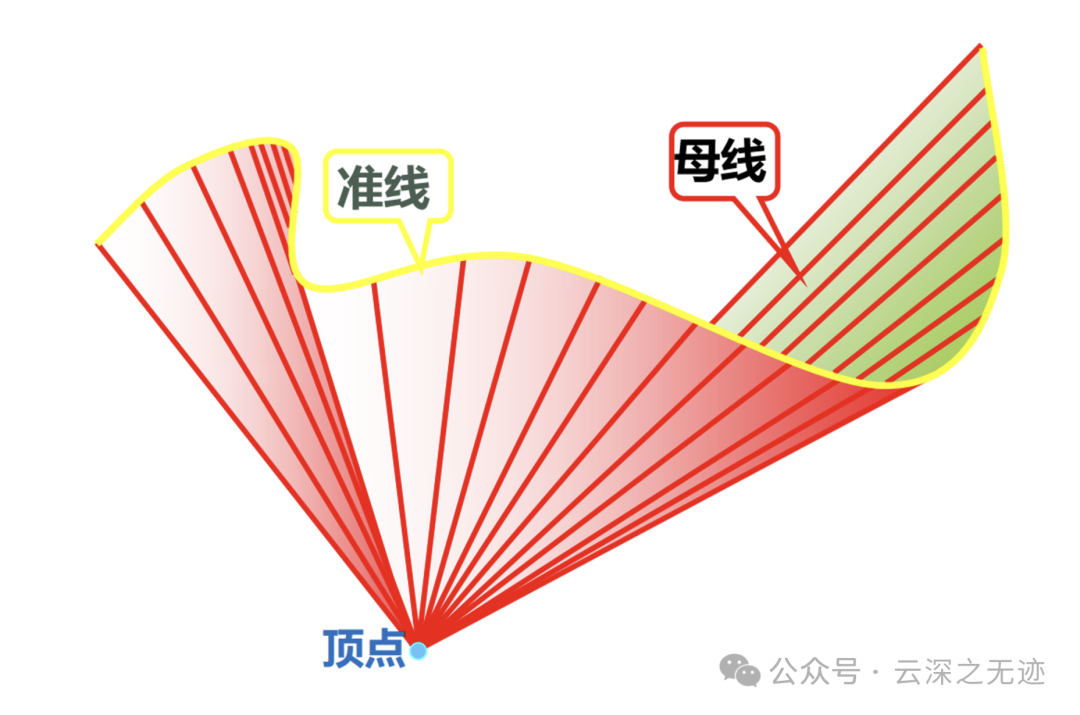
最广义的是这样的,就是沿着这个母线走完的样子
锥面是指一个平面曲线绕其平面内的一条定直线旋转一周所形成的曲面。这条定直线称为锥面的轴,平面曲线称为锥面的母线。
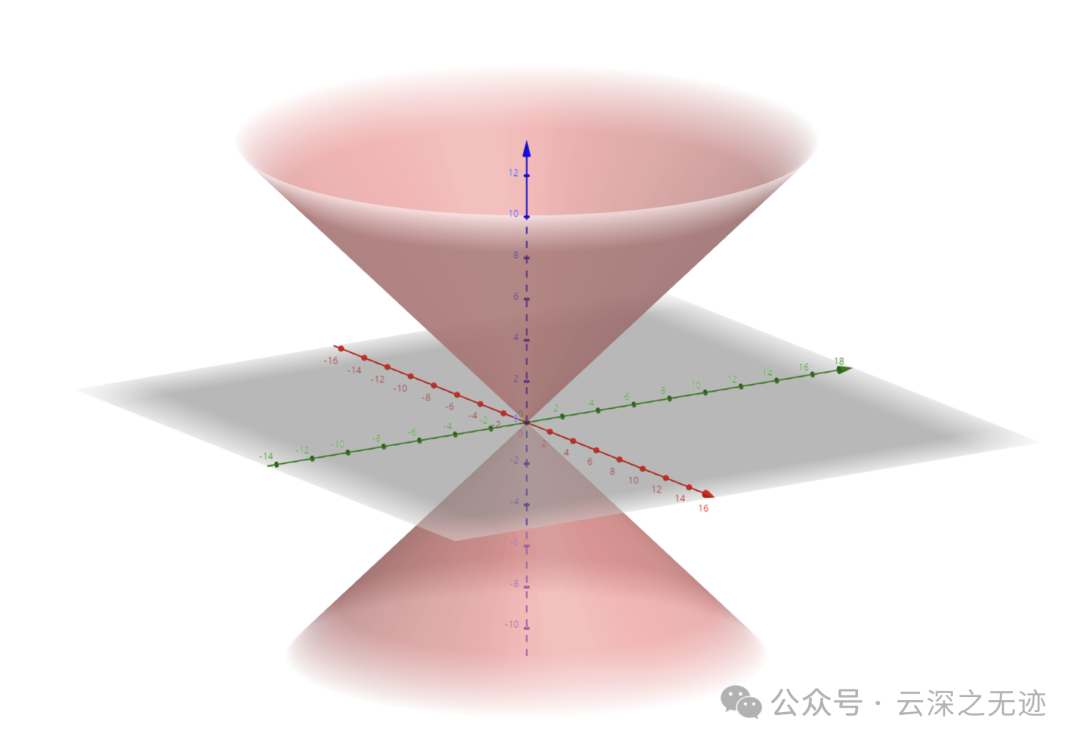
但是这个做题里面一般出现的是圆锥面
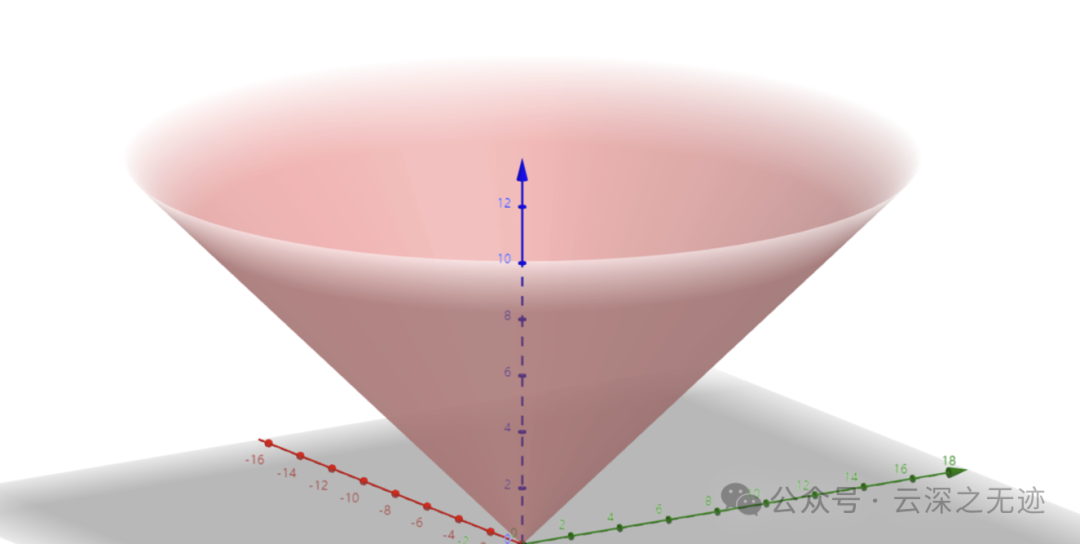
取一半儿又叫拌嘴面
一般方程:
(x^2 + y^2) / a^2 = z^2 / h^2其中,a为圆锥底面半径,h为圆锥高。
标准方程:
x^2 + y^2 = z^2 * tan^2α其中,α为圆锥母线与轴的夹角。这是书上的做法,做题根本就不是这样的,我真的服了。
z=√3(x^2+y^2) 是什么样子?
z 与 x² + y² 的关系: z 的值直接与 x² + y² 的值成正比。这意味着,当 x 和 y 的值固定时,z 的值也固定,且 z 始终为非负值。
圆的方程: x² + y² = r² 表示以原点为圆心,半径为 r 的圆。
z 的变化: 随着 x 和 y 的变化,x² + y² 的值也会变化,从而导致 z 的值也随之变化。但是,对于固定的 z 值,x² + y² 的值是一个常数,即在 z = k 的平面上,截面是一个圆。
锥形特征: 随着 z 值的增大,圆的半径也随之增大,形成一个向上开口的圆锥形。
类似于一个冰淇淋筒的形状。在不同高度的水平面上截取,得到的截面都是圆。锥角的大小取决于系数 √3。
方程 z = √3(x² + y²) 描述了一个以 z 轴为对称轴的圆锥面,其顶点位于原点。
搞明白没有?