概率论中的卷积和信号与系统中卷积的联系 这是以前写的,时间线有点混乱。
信号与系统,里面研究系统在一个确定信号的激励下有什么反应。给定任意输入信号,求系统响应。
前面都是说很多的物理系统可以写成常系数微分方程,求解这个就可以。
但是还有一种是使用卷积和(离散),卷积积分(连续的)其实就是想表达,这个系统的响应的效果。
一个响应给到系统里面,肯定是一开始有个峰值,然后就随着时间就有个衰减的过程.
如果这个响应是按照一定的时间不停的加进来了的,然后我们就在一个位置看这个效果,不看别的地方,你会发现除了最强的峰,还有第二个响应衰减的一些量也出现在你观察的位置上面,接着就是第三个,第四个:
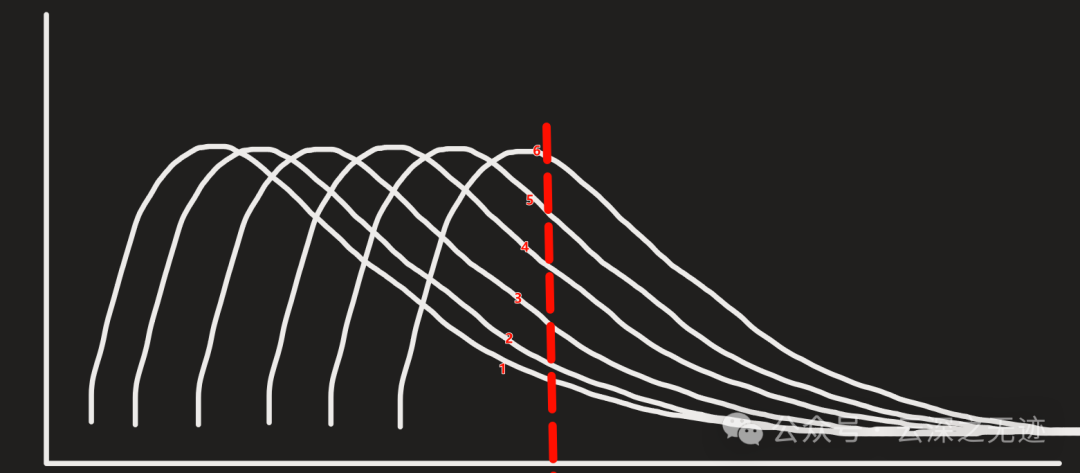
大概就是说一个地方的效果其实是不同时间波衰减到这个位置的叠加
一次能量进来以后,以衰减的形式影响到所有的输出。就好像是你在小时候读了一个故事,第一年你还记得很多,三年后可能你就记得大部分的故事,五年后还记得一些人物,10年后就记得一个标题,现在可能就知道以前还读过一个故事。这是一个故事的衰减,你总是记得住最近的东西,对离你时间久远的东西所遗忘,但就观察一个时间点,你总是由最近清晰的时间记忆和逐渐遗忘的记忆所构成。
是不是有些感觉了?假如我们就想五天的过程:

一天忘一点,最后第五天就是可以记得住第一天的内容的五分之一
那我们就像研究第一天的记忆量是什么?第五天以及的全部,第四天的五分之四,第三天的五分之三,第二天的五分之二,第一天的五分之一。

哈哈哈,这个卷积我想做很久了!搞一些小三角,每一个都是我们一天的记忆。

把他拍好,画一道,也就是我们要研究这个地方的效果

会看到,今天的记忆是由这些不断衰减的记忆构成

如果灯很宽,就可以看到所有的条在一个平面的不同分布
根据实验,我们先看两个极端的值,今天和前五天,效果是不是就是第一天的全部+第五天的一点。

就是这样,是不是不好看

我们把第五天翻转一下,这样看就好了,也就是计算里面的翻转

这个是移位

都要移动一次

然后叠加,懂了没有?没懂就搞六个三角形摆一摆
其实也可以找到一些内在联系:6+1=5+2=4+3=3+4=2+5=1+6

这里蕴含了一种约束和对应关系,f是对应要求的响应,g是过往的时间系统,我称为历史项。
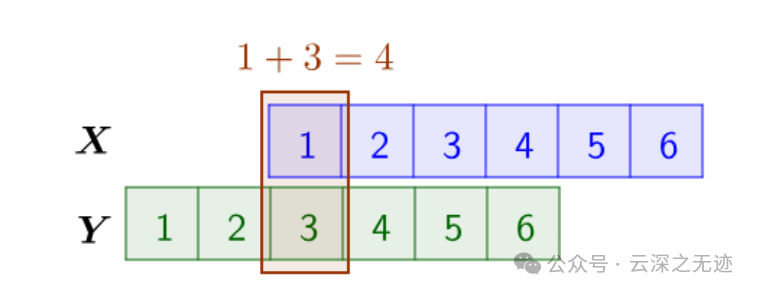
这样的
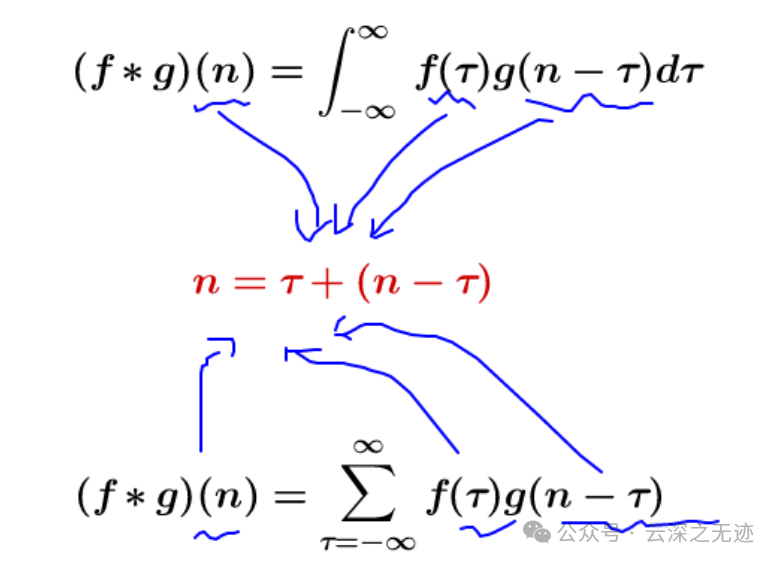
满足这样的翻转关系
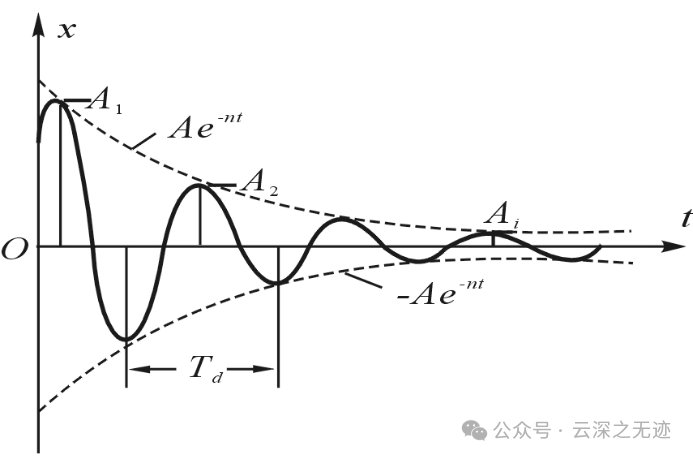
一个衰减的样子
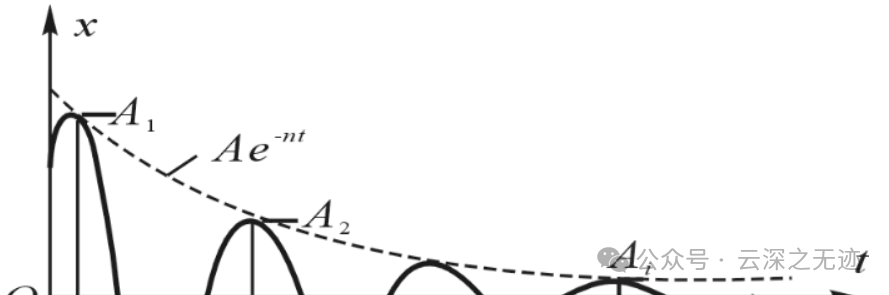
半个
对任意的x的响应是

一种新运算

这个你看看是不是就是我们的做法
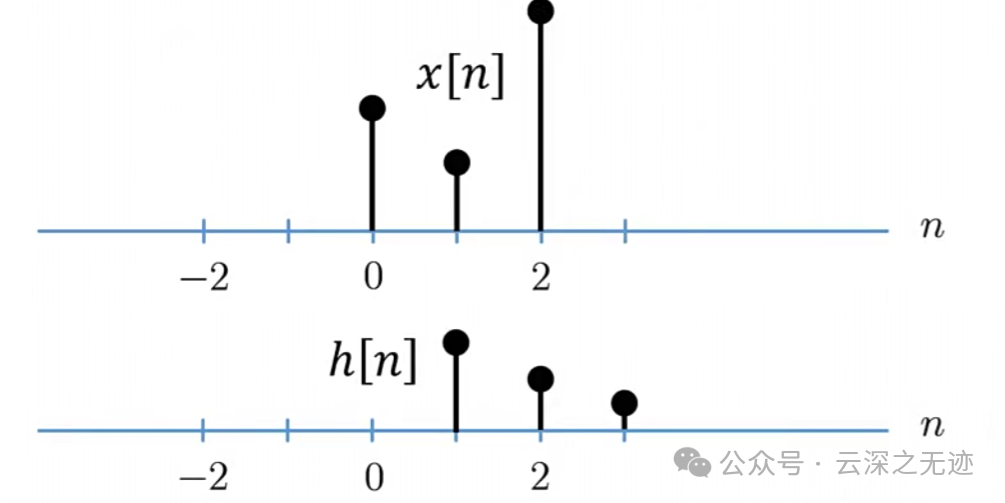
n
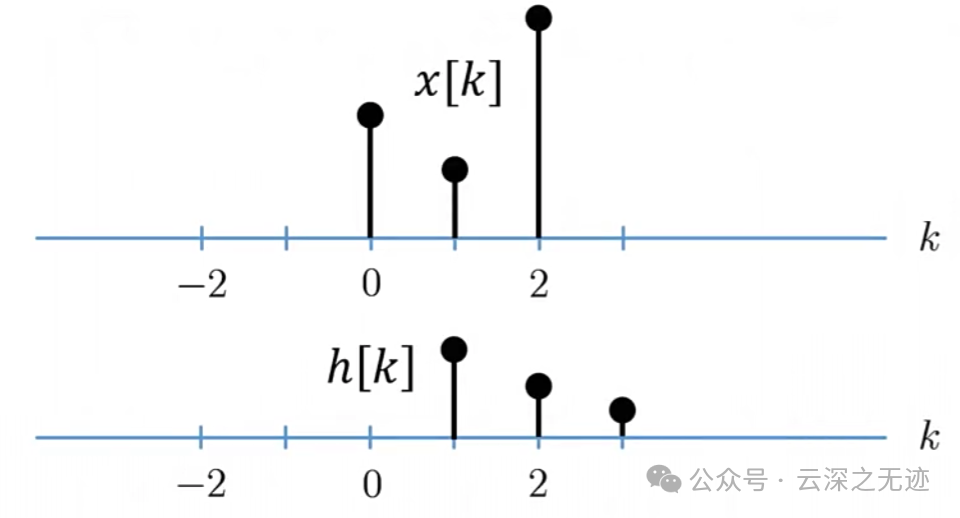
换k
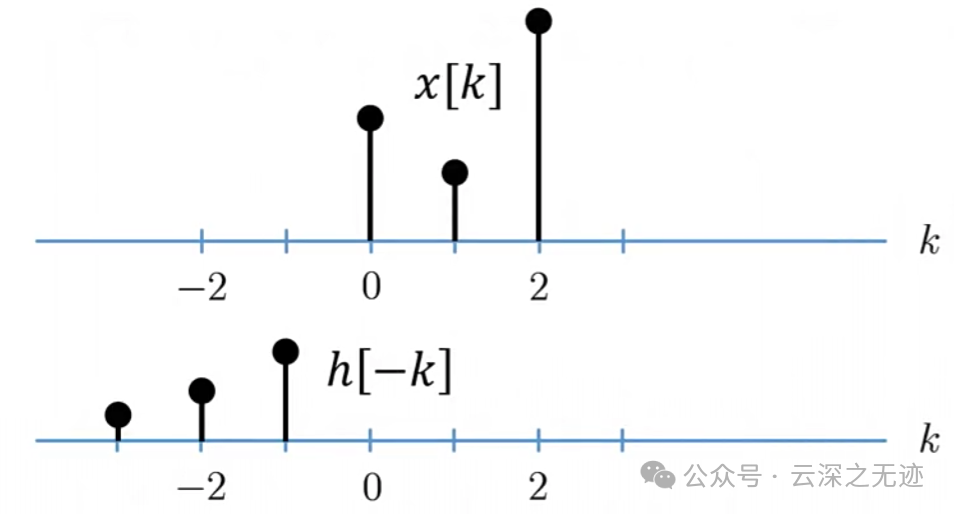
翻转
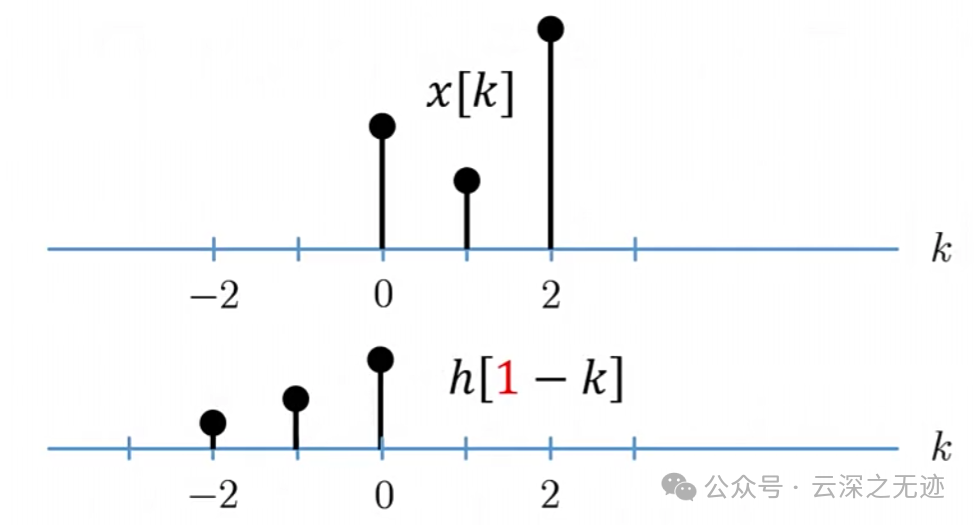
往右走
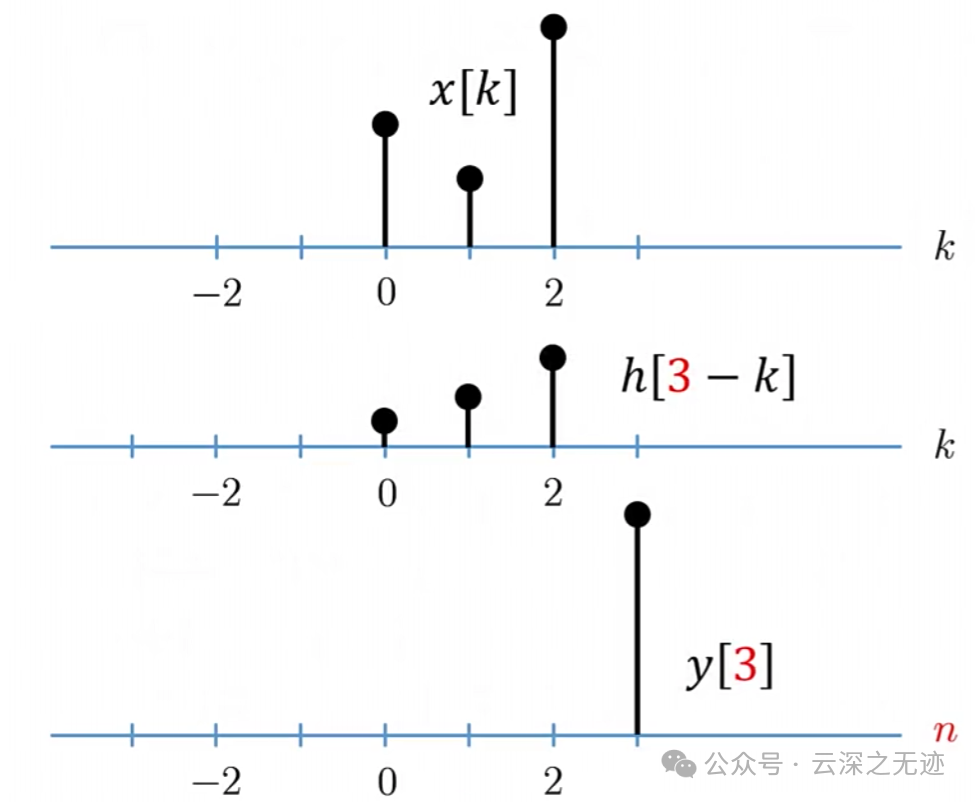
相加

概率统计里面也有
