连续，可偏导，可微之间的关系

1. 连续性就像一条路，没有断裂。

2. 可偏导性就像这条路上的一些局部路段有明确的坡度。

3. 可微性就像这条路在某一点附近可以近似看成一条直线。

在昨天的文章里面，王老师给挑出来了错误，这就是学习中的缺陷：

函数连续与某处函数值的关系,从一元到多元 在这篇的最后：

这个就是错误的结论

在原点处偏导数存在，但函数在原点不连续，因为不能取这个值。

f(x,y) = xy/(x^2+y^2)  (x^2+y^2≠0)

 f(0,0)=0 在原点处偏导数存在，但函数在原点不连续。（因为分母为0不行啊）。

关键是第一个：原点是连续的，但是偏导数在原点不存在。就是这个极限不存在

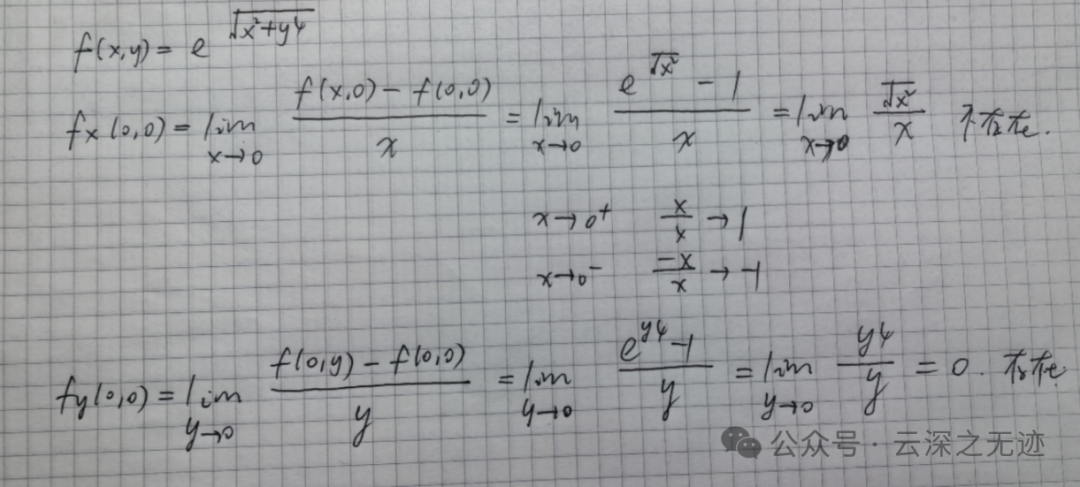
王老师是使用的定义写的，只是一个例子

连续不一定可偏导

可偏导也不一定连续，就我举的例子，分母为0的时候就不连续了，但是求极限是可以的，原点处也可以求导数。

1.连续性

一个函数在某点连续，直观上说就是函数的图像在该点没有“断裂”。更严格的定义是：当自变量趋近于该点时，函数值也趋近于该点处的函数值。函数图像在该点是连续的曲线。

2. 可偏导性

 一个多元函数在某点关于某个变量的偏导数存在，就称该函数在该点关于该变量可偏导。函数图像在该点沿坐标轴方向有切线。函数在某个特定方向上的变化率。

3. 可微性

一个多元函数在某点可微，意味着该函数在该点附近可以用一个线性函数来近似。函数图像在该点附近可以看作是一个切平面。

可微一定连续: 如果一个函数在某点可微，那么它在该点一定连续。这是因为可微性隐含了函数在该点附近的变化可以用一个线性函数来近似，而线性函数是连续的.

可微性是比前两者更强的概念，它描述了函数在某点附近的局部性质。

• 连续性是可微性的必要条件，因为如果一个函数在某点不连续，那么它在该点附近的变化就无法用一个线性函数来近似。

• 可偏导性是可微性的一个方面，但不是全部。可微性要求函数在所有方向上的变化都能用一个线性函数来近似。

还有一个知识点是，在一点处的偏导数怎么求？

一个多元函数 z=f(x,y)，在点 (x0,y0) 处，关于 x 的偏导数定义为：

∂f/∂x|_(x0,y0) = lim(h→0) [f(x0+h, y0) - f(x0, y0)] / h

关于 y 的偏导数定义：

∂f/∂y|_(x0,y0) = lim(k→0) [f(x0, y0+k) - f(x0, y0)] / k

固定其他变量: 在求关于 x 的偏导数时，我们将 y 看作常数，只让 x 发生变化，然后求在这个方向上的导数。

1. 确定求导点: 明确要求偏导数的点 (x0,y0)。
2. 固定其他变量: 将函数中除了要求导的变量外的其他变量都看作常数。
3. 代入定义: 将函数代入偏导数的定义式中。

求导点：(x0,y0)=(1,2)。固定 y：将 y 看作常数2。

∂f/∂x|_(1,2) = lim(h→0) [(1+h)^2*2 - 1^2*2] / h

计算极限：

= lim(h→0) (2h + 2h^2) / h= lim(h→0) (2 + 2h)= 2

所以，函数 f(x,y) 在点 (1,2) 处关于 x 的偏导数为 2。