反函数，复合函数，初等函数的连续性

初等函数是指由常数函数、幂函数、指数函数、对数函数、三角函数以及它们的有限次复合而成的函数。

所有初等函数在其定义域内都是连续的。

这意味着：

初等函数的图像是一条连续不断的曲线，没有间断点。

初等函数在定义域内的任意一点，其函数值都等于其在该点的极限值。

 对于初等函数，我们可以直接代入求值，而不需要考虑左右极限是否相等。

常见的初等函数及其连续性

1. 常数函数： y=c (c为常数) 在整个实数范围内连续。

2. 幂函数： y=x^n (n为有理数) 在其定义域内连续。

3. 指数函数： y=a^x (a>0且a≠1) 在整个实数范围内连续。

4. 对数函数： y=log_a(x) (a>0且a≠1) 在(0, +∞)内连续。

5. 三角函数： sinx, cosx, tanx, cotx, secx, cosecx 在各自的定义域内连续。

   
   

反函数的连续性：

如果一个严格单调函数f(x)在区间I上连续，且在该区间上存在反函数g(x)，那么g(x)在区间f(I)上也是连续的。

连续函数的图像是一条不间断的曲线。如果一个函数是严格单调的，那么它的图像不会出现“折返”的情况。因此，它的反函数的图像也同样是一条不间断的曲线，即反函数也是连续的。

这个反函数的图像是关于x=y对称的，所以这个严格的对称性也可以不证明，然后就记住显然的结论就行。

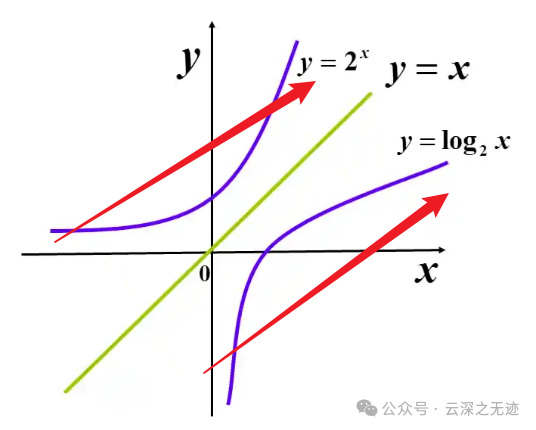
这个对称性就

复合函数的连续性：

如果函数g(x)在点x=a处连续，且函数f(u)在点u=g(a)处连续，那么复合函数f(g(x))在点x=a处也连续。

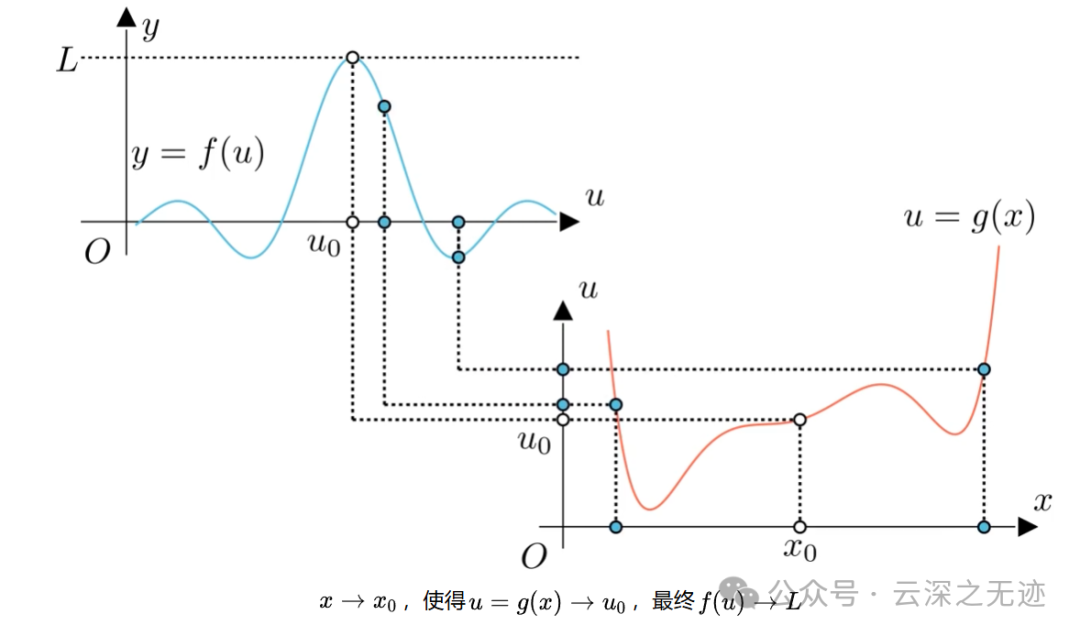
 复合函数可以看作是一个函数的输出作为另一个函数的输入。如果两个函数在各自的定义域内都是连续的，那么复合后的函数也应该保持连续性。就是一个函数的Y变成了另外一个函数的X，就好像单片机定时器里面的级联一样。

反函数: 函数f(x) = x^3在整个实数集上是严格单调递增的连续函数，因此它的反函数g(x) = ∛x在整个实数集上也是连续的。

复合函数: 函数f(x) = sinx和g(x) = x^2都是连续函数，因此它们的复合函数f(g(x)) = sin(x^2)也是连续的。

复合函数的连续性: 复合函数的连续性取决于内外两个函数在各自的定义域内的连续性。

反函数的存在性: 只有严格单调的函数才存在反函数。